视觉SLAM笔记--第6篇: 单目初始化和三角测量

参考博客

参考博客：https://blog.csdn.net/llfjcmx/article/details/83410318

1. 三角测量

在得到了相机的运动之后，下一步我们需要用相机的运动来估计特征点的空间位置，但是在单目SLAM中，仅通过单张图像是无法获得像素的深度信息的，需要用三角测量（三角化）的方法来估计地图点的深度。

三角测量是指通过在两处观察同一个点的夹角，来确定该点的距离。

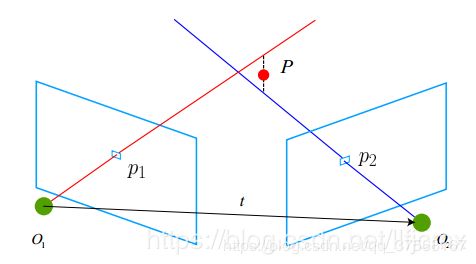
考虑图像$I_1,I_2$，相机的光心为$o_1,o_2$，以左图为参考，右图的变换矩阵为$R,t$。

假设在$I_1$中有特征点$p_1$，对应到$I_2$中的特征点$p_2$，理论上讲$o_1{p}_1和o_2{p}_2$会相交于某一点P，该点即是两个特征点所对应的地图点在三维场景中的位置，但是由于噪声的影响，这两条直线往往无法相交，因此可以通过最小二乘法来求解出距离最近的那个点作为相交点。

按照对极几何中的定义，如果设$x_1,x_2$为两个特征点的归一化坐标，于是有下列关系式：
$$s_1{x}_1=s_2{x}_{2}R+t$$已知：坐标系$o到o_1$的变换矩阵$R、t$归一化坐标$x_1,x_2$，现在要求的就是两个特征点的深度$s_1,s_2$

左乘$[x_1{]}_{\times }$可得$s_1[x_1{]}_{\times }{x}_1=0$：
$$s_2[x_1{]}_{\times }{x}_{2}R+[x_1{]}_{\times }t=0$$可以解出$s_2$, 将其带入原来的式子可解出$s_1$.
但是，由于噪声的存在，我们求出来的R,t不一定能够使得上式精确等于0，因此在实际情况中，更常见的做法是求最小二乘解而不是零解。

2. 单目初始化

由于 E(本质矩阵)本身具有尺度等价性,它分解得到的 $R、t$也有一个尺度等价性。而本身具有约束,所以我们认为 $t$ 具有一个尺度。换言之，在分解过程中，对t乘以任意非零常数，分解都是成立的。因此，我们通常把t进行归一化，让它的长度等于1.

对 $t$ 长度的归一化，直接导致了单目视觉的尺度不确定性。因为对t乘以任意一个比例常数后，对极约束仍然是成立的。换言之，在单目SLAM中，对轨迹和地图同时缩放任意倍数，我们得到的图仍然是一样的。

单目视觉的初始化问题

在单目视觉中，我们对两张图像的t进行归一化，相当于固定了一个尺度。虽然我们不知道它的实际长度是多少，但是我们可以以这时的 $t$ 为单目1，计算相机运动和特征点的3D位置，这一步称为单目SLAM的初始化。

在初始化之后，就可以用3D-2D来计算相机的运动了，初始化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，初始化也是单目SLAM中不可避免的一个步骤。

初始化的两张图片必须要有一定程度的平移，而后的轨迹和地图都将会以这一步的平移为单位。单目初始化不能只有纯旋转，必须要有一定程度的平移，如果没有平移，单目将无法初始化。

3. 单目-双目/RGB-D初始化的比较

1. 初始化的目的是建立三维的空间点和地图并为之后的计算提供初始值；
2. 同双目/RGB-D SLAM不同，单目SLAM无法从一帧图片中计算出深度，因此初始化需要两帧连续满足条件的图片来进行初始化；
3. 单目SLAM初始化计算位姿是一个对极约束问题，而双目/RGB-D SLAM的初始化计算位姿是一个PnP问题；
4. 在初始化成功后单目SLAM和双目SLAM一样是通过PnP来求解相机位姿的；
5. 单目SLAM尺度不确定性的原因是因为在通过SVD分解E矩阵求解R，t时计算的t是没有单位的；
6. 单目SLAM初始化的过程中对t进行了归一化来固定尺度，即以求解的初始帧的t为单位1，而后的轨迹和平移都将以这个t为单位；
7. 单目SLAM的初始化一定要有一定程度的平移，纯旋转是无法完成初始化的。

4. 单目初始化两种方法

单目初始化的两种方法：使用基本矩阵F（极限约束），或是单应性矩阵H（平面结构）进行初始化。

从 E 分解到 R; t 的过程中，如果相机发生的是纯旋转，导致 t 为零，那么，得到的E 也将为零，这将导致我们无从求解 R。不过，此时我们可以依靠 H 求取旋转，但仅有旋转时，我们无法用三角测量估计特征点的空间位置（这将在下文提到），于是，另一个结论是， 单目初始化不能只有纯旋转，必须要有一定程度的平移。如果没有平移，单目将无法初始化。