2020牛客多校第四场补题

B.Basic Gcd Problem

解析:
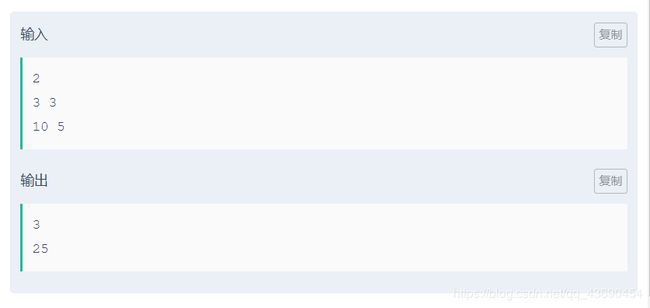
分解出n的质因数个数为cnt
答案:c^cnt %MOD

#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=1e9+7;
int t;
int n,c;
inline int read(){
    int sgn = 1; int cnt = 0; 
    char ch = getchar();
    while (ch < '0' || ch > '9') {    
        if(ch == '-')
            sgn = -sgn;
        ch = getchar();
    }
    while ('0' <= ch && ch <= '9') {
        cnt = cnt*10 + (ch-'0');
        ch = getchar();
    }
    return  sgn*cnt;
}
ll quick(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return res;
}
int main()
{
    t=read();
    while(t--)
    {
        n=read();c=read();
        int  ans=0;
        for(int i=2;i<=n/i;i++){
            if(n%i==0)
            {
                while(n%i==0) ans++,n/=i;
            }
        }
        if(n>1) ans++;
        printf("%d\n",quick(c,ans)%MOD);
    }
 }

F. Finding the Order


解析: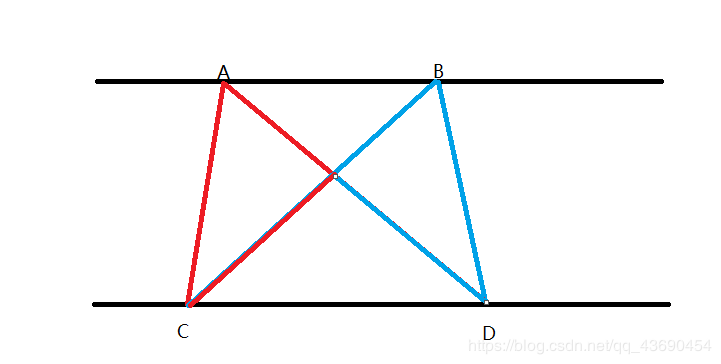
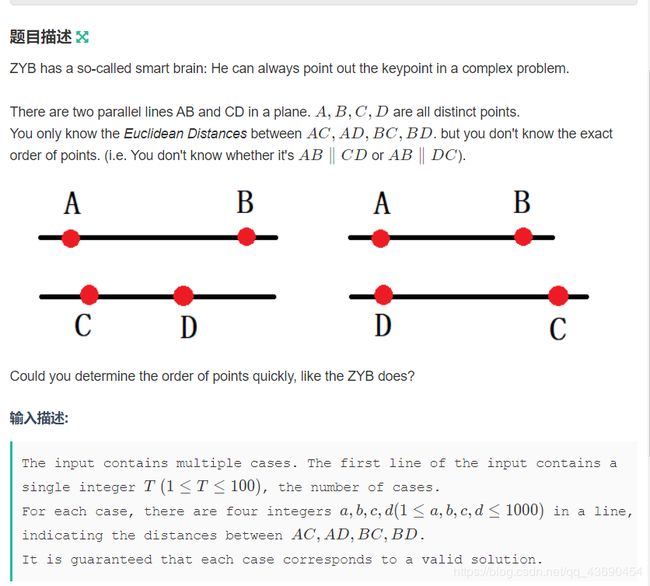
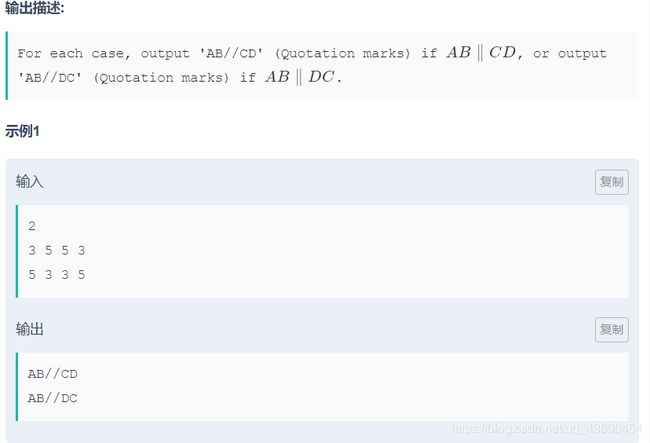
根据三角形两边之和大于第三边这个性质
那么AD+BC>AC+BD 这样AB//CD
如果AD+BC 所以AB//DC

#include<bits/stdc++.h>
using namespace std;
int t,a,b,c,d;
int main()
{
	cin>>t;
	while(t--)
	{
		cin>>a>>b>>c>>d;
		if(b+c>a+d) cout<<"AB//CD"<<endl;
		else cout<<"AB//DC"<<endl; 
	}
}

H.Harder Gcd Problem


解析:
贪心。我们把n分解出质因数。不同质因数与它的倍数可以组成一对。所以我们只要枚举前n/2个质因数。
但是我们不能从小到大枚举每个质因数的倍数，因为有可能最大的质因数的与它的倍数无法组成一队
假设 n=8
质因数为 2,3,5,7.但我们只取2,3这两个质因数(因为5和7的倍数一定大于n)
2可以枚举的倍数分别为 2,4,6,8 那么可以组成2对 (2,4),(6,8)
3可以枚举的倍数分别为 3,6 这时候因为6被用了，所以不能组成一对 这样答案不一定最优了

所以我们需要贪心从大往小贪质因数。对于每个质因数p可以枚举倍数的个数为x 如果x为奇数，我们把 2*p留下来，等待后续匹配
举个例子n=9
质因数为2,3,5,7 我们只取2,3
3可以枚举的倍数分别为3,6,9 根据上述我们要把6留下来 所以(3,9)匹配
2可以枚举的倍数分别为2,4,6,8 根据上述我们可以组成(2,6),(4,8）6留下来就是现在匹配的

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10000;
int prime[N],cnt,t,n;
int num[N];
bool st[N];
void init()
{
	memset(st,false,sizeof st);
	for(int i=2;i<N;i++)
	{
		if(!st[i]) prime[++cnt]=i;
		for(int j=1;j<=cnt&&prime[j]<=N/i;j++){
			st[prime[j]*i]=true;
			if(i%prime[j]==0) break;
		}
	}
	 
} 
int main()
{
	init();
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++) st[i]=false;
		memset(num,0,sizeof num);
		int tot=0;
		int mx=upper_bound(prime+1,prime+1+cnt,n/2)-prime-1;
		for(int i=mx;i>=1;i--)
		{
			for(int j=prime[i];j<=n;j+=prime[i])
			{
				if(st[j]) continue;
				if(j==2*prime[i]) continue;
				num[++tot]=j;
				st[j]=true;
			}
			if(tot&1) num[++tot]=2*prime[i],st[2*prime[i]]=true;
		}
		printf("%d\n",tot/2);
		for(int i=1;i<=tot;i+=2) 
		{
			printf("%d %d\n",num[i],num[i+1]);
		}
	 } 
 }