Frozen_Guardian
Frozen_Guardian

牛客多校3 - Fraction Construction Problem(扩展欧几里得)

题目链接：点击查看

题目大意：给出 a 和 b ，求解满足条件的 c,d,e,f ，使得：

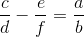
  1. \frac{c}{d}-\frac{e}{f}=\frac{a}{b}
  2. d < b
  3. f < b
  4. c,e 均为小于等于 4e12 的正整数

题目分析：分情况讨论一下，首先如果 a 和 b 可以约分的话，那么直接约分后，输出 a+1 , b , 1 , b 显然就是答案了，如果不能约分的话，且 b 的相异质因子的个数不超过 1 个的话，那么是无解的，证明如下：（来自官方题解）

牛客多校3 - Fraction Construction Problem(扩展欧几里得)_第1张图片

最后一种情况就是 b 的相异质因子个数超过一个，对于这种情况可以将条件 1 的公式转换一下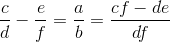： \frac{c}{d}-\frac{e}{f}=\frac{a}{b}=\frac{cf-de}{df}

这样一来，d 和 f 显然就是 b 的两个相异质因子了，而 cf - de = a ，在已知 d 和 f 的前提下，一定有解，且可以用扩展欧几里得来解决，注意最后求出来的答案需要处理一下，因为需要保证 c 和 e 为正整数

在找 d 和 f 的时候也有技巧，如果 sqrt( n ) 暴力去找的话，会超时，所以可以用埃氏筛预处理一下，保存一下每个数字的最大质因子，这样就可以令 d 为该质因子的幂，然后 f = b / d 了

代码：
 

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
 
typedef long long LL;
 
typedef unsigned long long ull;
 
const int inf=0x3f3f3f3f;
 
const int N=2e6+100;

int pri[N];//pri[i]:i的最大质因子为pri[i]
 
template void exgcd(T a,T b,T &d,T &x,T &y){
    if(!b) {d=a;x=1;y=0;}
    else {exgcd(b,a%b,d,y,x);y-=x*(a/b);}
}
//求解二元一次方程 a*x+b*y=c,一组解为x,y,无解则返回false
template bool Solve_equation(T a,T b,T c,T &x,T& y){
    T gcd;
    exgcd(a,b,gcd,x,y);
    if(c%gcd) return false;   //无解
    T k=c/gcd;
    x*=k;y*=k;
    T xplus=b/gcd,yplus=a/gcd; 
    if(xplus<0) xplus*=-1;if(yplus<0) yplus*=-1;
    //此时求出的x,y即为一组解，该方程的通解形式为X=x+t*(b/gcd),Y=y-t*(a/gcd) t为任意正整数
    //根据题目要求我们需要构造特殊解
    //x=(x%xplus+xplus)%xplus;y=c-a*x; //x的最小正整数解
    //y=(y%yplus+yplus)%yplus;x=c-b*y; //y的最小正整数解
    return true;
}

void init()
{
    pri[1]=1;
    for(int i=2;i>w;
    while(w--)
    {
        LL a,b;
        scanf("%lld%lld",&a,&b);
        LL gcd=__gcd(a,b);
        a/=gcd,b/=gcd;
        if(gcd!=1)
        {
            printf("%lld %lld %lld %lld\n",a+1,b,1,b);
            continue;
        }
        LL d=1,f=b;
        while(pri[b]!=1&&f%pri[b]==0)
        {
            f/=pri[b];
            d*=pri[b];
        }
        if(f==1)//只有一个质因子 
        {
            printf("-1 -1 -1 -1\n");
            continue;
        }
        LL c,e;
        Solve_equation(f,-d,a,c,e);
        LL k=abs(min(c/d,e/f))+1;
        c+=d*k,e+=f*k;
        printf("%lld %lld %lld %lld\n",c,d,e,f);
    }
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
    return 0;
}

 

你可能感兴趣的:(数论)

  • 致良知之寄诸用明书 BonSun
    众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
  • Python【math数学函数】 Alan_Lowe #Pythonpython
    Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • 算法设计与分析学习（6）——数论 罗塞菈桔梨萝柚 算法学习算法线性代数
    数论整除基本概念若aaa和bbb为整数，且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq，那么就说aaa可以整除bbb或是bbb被aaa整除，记作a∣ba|ba∣b。aaa也被称为bbb的约数，bbb也被称为a的倍数。若bbb不能被aaa整除，则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1，且除了±1,±p±1,±p±1,±p外没有其他的约数
  • 数论——欧几里得算法 NarutoTime 数论算法c++数据结构c语言
    1.欧几里得简介    欧几里得（希腊文：Ευκλειδης，约公元前330年—公元前275年），古希腊数学家，被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础，在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于：求解a和b的最大公约数。最大公约数英文为：Gre
  • 数论——扩展欧几里得算法 NOI_yzk
    欧几里得&拓展欧几里得（Euclid&Extend-Euclid）欧几里得算法（Euclid）背景：欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。——百度百科代码：递推的代码是相当的简洁：intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析：方法说了是辗转相除法，自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈？实际上在
  • 数论学习1（欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术） new出新对象！ 数学数算法学习
    目录1.唯一分解定理2.欧几里德算法（求最大公约数）3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少，(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式，乘法逆元，费马小定理今天也是小小的开始学习数论方面的知识了，首先数论的入门章节必然
  • Collatz 猜想和 Python 不连续小姐
    PythonDay4:CollatzConjecture原来总有学生问我，微积分有什么用啊，我说如果微积分学好了，也许抽象代数和数论就能学好，那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem，费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
  • 初等数论--整除--带余除法 WeidanJi 初等数论数学密码学信息安全
    初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论（整除+同余+原根），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。我整理成一个系列：初等数论，方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0，∃c∈Z,使a=bc,则称b整除a
  • 河南萌新2024第四场 Pown_ShanYu 算法数据结构
    C岗位分配题目大意：有n个岗位，m位志愿者，每个岗位至少需要a个志愿者，并且可以有志愿者可以空闲下来作预备，给出可能的分配情况总数思路：首先将每个岗位分配好至少需要的志愿者，再将剩下的人进行分配，那就满足球同盒不同模型（允许空盒），可用隔板法进行分配，需要额外开设一个空闲岗位用来预备，那么按照4个人去4个岗位，那么为c73，具体操作可看数论模板中发布的隔板法问题，递归求组合数Solved：intn
  • 【读书笔记】吴非《致青年教师》(4) 冬儿菇凉
    一、精要摘录(48——106页)1.教育教学不能“唯分数论“，比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感，心中有学生才会很在意学生对他的态度，在意学生的接受度。3.作为教师，你要善于向学生问出有意思的问题。4.教育就是要培养好习惯，教是为了达到不需要教学生，不需要老师教了是教学的成功，也是教师的职业追求。5.教师是学习者，在学习上教师首先要郑重其事，学生才有可能养成敬
  • 【代码随想录算法训练营Day39】62.不同路径；63. 不同路径 II 想做一只潜水的猪 算法
    文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难
  • 算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II memolaner 算法训练营算法动态规划数据结构c++python
    今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难想到。代码随想录视频讲解：动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示，第一直觉就是一个组合数的问题，学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成，重点是把二维的动态规划
  • 牛客周赛 Round 35（A,B,C,D,E,F,G） 邪神与厨二病 牛客算法暴力c++数论滑动窗口单调队列贪心构造
    这场简单，甚至赛时90分钟不到就AK了。比赛链接，队友题解友链刚入住学校监狱，很不适应，最近难受的要死，加上最近几场CF打的都不顺利，san值要爆掉了，只能慢慢补题了。这场C是个滑动窗口，D是贪心，E是有点麻烦的构造，FG是数论。A小红的字符串切割思路：记录一下字符串长度，然后从中间拆开。code：#include#include#includeusingnamespacestd;strings;
  • 算法——数论——同余 戏拈秃笔 数据结构与算法（java版）算法
    目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余：若m（正整数），a和b是整数，a%m==b%m，或(a-b)%m==0，记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程，解法看下面第一题二元线性丢番图方程逆：的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
  • pku acm 题目分类 moxiaomomo 算法数据结构numbers优化calendarcombinations
    1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
  • C++STL之Queue容器 芯片烧毁大师 数据结构C++c++开发语言
    C++STL之Queue容器1.再谈队列回顾一下之前所学的队列，队列和栈不同，队列是一种先进先出的数据结构，STL的队列内容极其重要，虽然内容较少但是请务必掌握，STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件：#include3.初始化格式为：**explicit**queue(**const**container_type&ctnr=container_t
  • 数字签名算法MD5withRSA Just_Paranoid 技术流Clipmd5rsasignatrue
    数字签名MD5withRSA，：将正文通过MD5数字摘要后，将密文再次通过生成的RSA密钥加密，生成数字签名，将明文与密文以及公钥发送给对方，对方拿到私钥/公钥对数字签名进行解密，然后解密后的，与明文经过MD5加密进行比较，如果一致则通过使用Signature的API来实现MD5withRSARSA原理：RSA算法基于一个十分简单的数论事实，将两个大素数相乘十分容易，但反过来想要对其乘积进行因式分
  • 2301: 不定方程解的个数 jht0105 算法
    题目描述输出不定方程解的个数。在数学中，不定方程是数论中的一个重要课题，在各种比赛中也常常出现.对于不定方程，有时我们往往只求非负整数解，现有方程ax+by+c=0，其中x、y为未知量且不超过10000，当给定a、b、c的值以后，可求出n组x、y的非负整数解，n>=0，,其中a，b，c均为[-10000,10000].输入描述一行，三个空格隔开的整数，为a、b、c的值。输出描述一个整数，为合法的解
  • python伯努利多项式 微小冷 #sympypython开发语言sympy伯努利数排列组合符号计算
    文章目录伯努利数和多项式sympy实现伯努利数是一种在数学、物理和工程中广泛应用的特殊数列，以瑞士数学家雅各布·伯努利（JacobBernoulli）的名字命名，并在许多领域中发挥重要作用。在数学中，它们与斐波那契数列、卡塔兰数、贝尔数等数列有密切联系，可以用于解决循环问题、组合问题和递推关系等数学问题。伯努利数和多项式伯努利(Bernoulli)数是一组在数论和复分析中出现的数，与伯努利多项式有
  • 二次剩余问题x的求解及代码实现（python） JustGo12 数论安全1024程序员节
    一、问题引入二次剩余是数论基本概念之一。它是初等数论中非常重要的结果，不仅可用来判断二次同余式是否有解，还有很多用途。C.F.高斯称它为算术中的宝石，他一人先后给出多个证明。[1]研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用，包括从噪音工程学到密码学以及大数分解。即关于方x^2≡a(modp)对于这个方程，求出满足条件的x。二、x的求解在上述问题下，根据p值的不同性质，可以
  • 【数论】exgcd 扩展欧几里得算法 Texcavator 数论算法
    参考：exgcd详解-zzt1208-博客园(cnblogs.com)exgcd（扩展欧几里得算法），用来求形如ax+by=gcd(a,b)ax+by=gcd(a,b)ax+by=gcd(a,b)（a,ba,ba,b为常数）的方程的一组整数解。（如果不确定等号右边是不是gcd，可以先当做gcd，求出来之后验证，是的话就是解，不是的话就不是解）推导见上面的链接，这篇只放个板子codeintexgcd
  • 2021-07-30 RX-0493
    学了一会数论，好难1.乘法逆元：a/b%p,若a/b在进行取模运算时，会出现精度问题，而且模运算对除法不适用，（没有分配律，大概就这意思）而求出乘法逆元后，可以把原式变为a*x%p的形式，且值不变。a*x≡1（modp）中，a,p为已知量，则x为a的乘法逆元。例题：乘法逆元设p=k*i+r,(1usingnamespacestd;constintN=20000530;intn,p,inv[N];i
  • 同余数论性质 clmm_ 算法
    同余概念当a%m==b%m，说明a和b同余，写作若a≡b(modm)性质衍生出几条性质1.m|abs(a-b)，即|a-b|是m的倍数。（注意，0是任何数的倍数）2.当a≡b(modm)，c≡d(modm)，有ac≡bd(modm)有a+c≡b+d(modm)有a-c≡b-d(modm)证明如下
  • 读《爱心与教育》第八天 皮_小皮
    作为一名教师，尤其是班主任老师，“培优转差”是教育工作的一项重要内容，读了李镇西老师的《爱心与教育》，自己受到不小的启发，对“优生”的培养和后进生的转化有了新的认识和思考。对“优生”的重新认识——李老师说：“优生”当然应该是指品学兼优的学生，但在现在不少教师、家长的眼中，所谓“优生”更多的是指学习成绩拔尖的学生（即尖子生）。的确，在升学竞争和应试教育的大环境下，很多教育者都以分数论英雄，对“优生”
  • RSA算法 superdont 图像加密算法java服务器
    RSA算法是一个非对称加密算法，它依赖于数论中的大整数因数分解问题的困难性。在RSA中，加密和解密使用不同的密钥，分别称为公钥和私钥。RSA算法的基本原理包括以下几个步骤：密钥生成：a.选择两个大的质数(p)和(q)。b.计算它们的乘积(n=pq)，n的长度就是密钥长度。c.计算欧拉函数(\phi(n)=(p-1)(q-1))。d.选择一个整数(e)，使得(1
  • 日精进110天 金八力韩英雪
    敬爱的老师，智慧的班主任，亲爱的跃友们：大家好！我是来自山峰教外教育的韩英雪，今天是我的日精进行动第110天，给大家分享我今天的进步，我们互相勉励，携手前行。每天进步一点点，距离成功便不远。1、比学习:个体身心发展的规律。顺序性，阶段性，不平衡性，互补性，个别差异性和整体性。个体身心发展的能动动因主要由内发论，外数论多因素互相作用论。其中内发论的代表人物包括孟子，弗洛伊德，威尔逊，格赛尔，霍尔等外
  • [C语言]Day04作业：输出菱形,判断水仙花数,输出a = aaaaa MrDorli C语言学习c语言
    /*1.在屏幕上输出以下图案：*************************************************************************************2.求出0～999之间的所有“水仙花数”并输出。“水仙花数”是指一个三位数，其各位数字的立方和确好等于该数本身，如；153＝1＋5＋3?，则153是一个“水仙花数”。在数论中，水仙花数（Narciss
  • 信安数基2-同余方程 利賀田
    基本概念及一次同余式同余式是数论的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m|(a-b)，则称a与b对模m同余，记为a≡b(modm)，或记为a≡b(m)。这个式子称为模m的同余式，若m∤(a-b)，则称a、b对模m不同余，同余概念又常表达为：1.a=b+km(k∈Z)；2.a和b被m除时有相同的[余数]。同余式的记号由高斯(Gauss,C.F.)于1800年首创,发表在他的数论
  • 【数论】矩阵快速幂 Texcavator 数论矩阵算法数据结构
    参考：P3193[HNOI2008]GT考试题解放个板子structMartix{inta[30][30];//在这里修改矩阵的大小Martix(){memset(a,0,sizeof(a));}Martixoperator*(constMartix&B)const//乘法运算符重载{Martixres;for(inti=0;i>=1;a=a*a;}returnans;}
  • 遍历dom 并且存储（将每一层的DOM元素存在数组中） 换个号韩国红果果 JavaScripthtml
    数组从0开始！！ var a=[],i=0; for(var j=0;j<30;j++){ a[j]=[];//数组里套数组，且第i层存储在第a[i]中 } function walkDOM(n){ do{ if(n.nodeType!==3)//筛选去除#text类型 a[i].push(n); //con
  • Android+Jquery Mobile学习系列(9)-总结和代码分享 白糖_ JQuery Mobile
    目录导航   经过一个多月的边学习边练手，学会了Android基于Web开发的毛皮，其实开发过程中用Android原生API不是很多，更多的是HTML/Javascript/Css。   个人觉得基于WebView的Jquery Mobile开发有以下优点： 1、对于刚从Java Web转型过来的同学非常适合，只要懂得HTML开发就可以上手做事。 2、jquerym
  • impala参考资料 dayutianfei impala
    记录一些有用的Impala资料   1. 入门资料 >>官网翻译：     http://my.oschina.net/weiqingbin/blog?catalog=423691   2. 实用进阶 >>代码&架构分析：     Impala/Hive现状分析与前景展望：http
  • JAVA 静态变量与非静态变量初始化顺序之新解 周凡杨 java静态非静态顺序
    今天和同事争论一问题，关于静态变量与非静态变量的初始化顺序，谁先谁后，最终想整理出来！测试代码： import java.util.Map; public class T { public static T t = new T(); private Map map = new HashMap(); public T(){ System.out.println(&quo
  • 跳出iframe返回外层页面 g21121 iframe
    在web开发过程中难免要用到iframe，但当连接超时或跳转到公共页面时就会出现超时页面显示在iframe中，这时我们就需要跳出这个iframe到达一个公共页面去。 首先跳转到一个中间页，这个页面用于判断是否在iframe中，在页面加载的过程中调用如下代码： <script type="text/javascript"> //<!-- function
  • JAVA多线程监听JMS、MQ队列 510888780 java多线程
    背景：消息队列中有非常多的消息需要处理，并且监听器onMessage（）方法中的业务逻辑也相对比较复杂，为了加快队列消息的读取、处理速度。可以通过加快读取速度和加快处理速度来考虑。因此从这两个方面都使用多线程来处理。对于消息处理的业务处理逻辑用线程池来做。对于加快消息监听读取速度可以使用1.使用多个监听器监听一个队列；2.使用一个监听器开启多线程监听。 对于上面提到的方法2使用一个监听器开启多线
  • 第一个SpringMvc例子 布衣凌宇 spring mvc
    第一步：导入需要的包； 第二步：配置web.xml文件 <?xml version="1.0" encoding="UTF-8"?> <web-app version="2.5" xmlns="http://java.sun.com/xml/ns/javaee" xmlns:xsi=
  • 我的spring学习笔记15-容器扩展点之PropertyOverrideConfigurer aijuans Spring3
    PropertyOverrideConfigurer类似于PropertyPlaceholderConfigurer，但是与后者相比，前者对于bean属性可以有缺省值或者根本没有值。也就是说如果properties文件中没有某个bean属性的内容，那么将使用上下文（配置的xml文件）中相应定义的值。如果properties文件中有bean属性的内容，那么就用properties文件中的值来代替上下
  • 通过XSD验证XML antlove xmlschemaxsdvalidationSchemaFactory
    1. XmlValidation.java package xml.validation; import java.io.InputStream; import javax.xml.XMLConstants; import javax.xml.transform.stream.StreamSource; import javax.xml.validation.Schem
  • 文本流与字符集 百合不是茶 PrintWrite()的使用字符集名字 别名获取
    文本数据的输入输出;           输入;数据流,缓冲流         输出;介绍向文本打印格式化的输出PrintWrite();   package 文本流; import java.io.FileNotFound
  • ibatis模糊查询sqlmap-mapping-**.xml配置 bijian1013 ibatis
            正常我们写ibatis的sqlmap-mapping-*.xml文件时，传入的参数都用##标识，如下所示： <resultMap id="personInfo" class="com.bijian.study.dto.PersonDTO"> <res
  • java jvm常用命令工具——jdb命令(The Java Debugger) bijian1013 javajvmjdb
            用来对core文件和正在运行的Java进程进行实时地调试，里面包含了丰富的命令帮助您进行调试，它的功能和Sun studio里面所带的dbx非常相似，但 jdb是专门用来针对Java应用程序的。         现在应该说日常的开发中很少用到JDB了，因为现在的IDE已经帮我们封装好了，如使用ECLI
  • 【Spring框架二】Spring常用注解之Component、Repository、Service和Controller注解 bit1129 controller
    在Spring常用注解第一步部分【Spring框架一】Spring常用注解之Autowired和Resource注解（http://bit1129.iteye.com/blog/2114084）中介绍了Autowired和Resource两个注解的功能，它们用于将依赖根据名称或者类型进行自动的注入，这简化了在XML中，依赖注入部分的XML的编写，但是UserDao和UserService两个bea
  • cxf wsdl2java生成代码super出错,构造函数不匹配 bitray super
        由于过去对于soap协议的cxf接触的不是很多,所以遇到了也是迷糊了一会.后来经过查找资料才得以解决. 初始原因一般是由于jaxws2.2规范和jdk6及以上不兼容导致的.所以要强制降为jaxws2.1进行编译生成.我们需要少量的修改: 我们原来的代码 wsdl2java com.test.xxx -client http://..... 修改后的代
  • 动态页面正文部分中文乱码排障一例 ronin47
    公司网站一部分动态页面，早先使用apache+resin的架构运行，考虑到高并发访问下的响应性能问题，在前不久逐步开始用nginx替换掉了apache。 不过随后发现了一个问题，随意进入某一有分页的网页，第一页是正常的（因为静态化过了）；点“下一页”，出来的页面两边正常，中间部分的标题、关键字等也正常，唯独每个标题下的正文无法正常显示。 因为有做过系统调整，所以第一反应就是新上
  • java-54- 调整数组顺序使奇数位于偶数前面 bylijinnan java
    import java.util.Arrays; import java.util.Random; import ljn.help.Helper; public class OddBeforeEven { /** * Q 54 调整数组顺序使奇数位于偶数前面 * 输入一个整数数组，调整数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半
  • 从100PV到1亿级PV网站架构演变 cfyme 网站架构
    一个网站就像一个人，存在一个从小到大的过程。养一个网站和养一个人一样，不同时期需要不同的方法，不同的方法下有共同的原则。本文结合我自已14年网站人的经历记录一些架构演变中的体会。 1：积累是必不可少的 架构师不是一天练成的。 1999年，我作了一个个人主页，在学校内的虚拟空间，参加了一次主页大赛，几个DREAMWEAVER的页面，几个TABLE作布局，一个DB连接，几行PHP的代码嵌入在HTM
  • [宇宙时代]宇宙时代的GIS是什么？ comsci Gis
           我们都知道一个事实，在行星内部的时候，因为地理信息的坐标都是相对固定的，所以我们获取一组GIS数据之后，就可以存储到硬盘中，长久使用。。。但是，请注意，这种经验在宇宙时代是不能够被继续使用的          宇宙是一个高维时空
  • 详解create database命令 czmmiao database
    完整命令 CREATE DATABASE mynewdb   USER SYS IDENTIFIED BY sys_password   USER SYSTEM IDENTIFIED BY system_password   LOGFILE GROUP 1 ('/u01/logs/my/redo01a.log','/u02/logs/m
  • 几句不中听却不得不认可的话 datageek
    1、人丑就该多读书。 2、你不快乐是因为：你可以像猪一样懒，却无法像只猪一样懒得心安理得。 3、如果你太在意别人的看法，那么你的生活将变成一件裤衩，别人放什么屁，你都得接着。 4、你的问题主要在于：读书不多而买书太多，读书太少又特爱思考，还他妈话痨。 5、与禽兽搏斗的三种结局：(1)、赢了，比禽兽还禽兽。(2)、输了，禽兽不如。(3)、平了，跟禽兽没两样。结论：选择正确的对手很重要。 6
  • 1 14:00 PHP中的“syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM”错误 dcj3sjt126com PHP
    原文地址：http://www.kafka0102.com/2010/08/281.html   因为需要，今天晚些在本机使用PHP做些测试，PHP脚本依赖了一堆我也不清楚做什么用的库。结果一跑起来，就报出类似下面的错误：“Parse error: syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM in /home/kafka/test/
  • xcode6 Auto layout and size classes dcj3sjt126com ios
    官方GUI   https://developer.apple.com/library/ios/documentation/UserExperience/Conceptual/AutolayoutPG/Introduction/Introduction.html   iOS中使用自动布局（一）   http://www.cocoachina.com/ind
  • 通过PreparedStatement批量执行sql语句【sql语句相同，值不同】 梦见x光 sql事务批量执行
    比如说：我有一个List需要添加到数据库中，那么我该如何通过PreparedStatement来操作呢？ public void addCustomerByCommit(Connection conn , List<Customer> customerList) {    String sql = "inseret into customer(id
  • 程序员必知必会----linux常用命令之十【系统相关】 hanqunfeng Linux常用命令
    一.linux快捷键 Ctrl+C : 终止当前命令 Ctrl+S : 暂停屏幕输出 Ctrl+Q : 恢复屏幕输出 Ctrl+U : 删除当前行光标前的所有字符 Ctrl+Z : 挂起当前正在执行的进程 Ctrl+L : 清除终端屏幕，相当于clear   二.终端命令 clear : 清除终端屏幕 reset : 重置视窗，当屏幕编码混乱时使用 time com
  • NGINX IXHONG nginx
    pcre 编译安装 nginx conf/vhost/test.conf   upstream admin { server 127.0.0.1:8080; }   server {                 listen       80; &
  • 设计模式--工厂模式 kerryg 设计模式
    工厂方式模式分为三种：   1、普通工厂模式：建立一个工厂类，对实现了同一个接口的一些类进行实例的创建。   2、多个工厂方法的模式：就是对普通工厂方法模式的改进，在普通工厂方法模式中，如果传递的字符串出错，则不能正确创建对象，而多个工厂方法模式就是提供多个工厂方法，分别创建对象。   3、静态工厂方法模式：就是将上面的多个工厂方法模式里的方法置为静态，
  • Spring InitializingBean/init-method和DisposableBean/destroy-method mx_xiehd javaspringbeanxml
    1.initializingBean/init-method 实现org.springframework.beans.factory.InitializingBean接口允许一个bean在它的所有必须属性被BeanFactory设置后，来执行初始化的工作，InitialzingBean仅仅指定了一个方法。 通常InitializingBean接口的使用是能够被避免的，（不鼓励使用，因为没有必要
  • 解决Centos下vim粘贴内容格式混乱问题 qindongliang1922 centosvim
    有时候，我们在向vim打开的一个xml，或者任意文件中，拷贝粘贴的代码时，格式莫名其毛的就混乱了，然后自己一个个再重新，把格式排列好，非常耗时，而且很不爽，那么有没有办法避免呢？ 答案是肯定的，设置下缩进格式就可以了，非常简单： 在用户的根目录下 直接vi  ~/.vimrc文件 然后将set pastetoggle=<F9> 写入这个文件中，保存退出，重新登录，
  • netty大并发请求问题 tianzhihehe netty
    多线程并发使用同一个channel java.nio.BufferOverflowException: null at java.nio.HeapByteBuffer.put(HeapByteBuffer.java:183) ~[na:1.7.0_60-ea] at java.nio.ByteBuffer.put(ByteBuffer.java:832) ~[na:1.7.0_60-ea]
  • Hadoop NameNode单点问题解决方案之一 AvatarNode wyz2009107220 NameNode
    我们遇到的情况 Hadoop NameNode存在单点问题。这个问题会影响分布式平台24*7运行。先说说我们的情况吧。 我们的团队负责管理一个1200节点的集群(总大小12PB)，目前是运行版本为Hadoop 0.20，transaction logs写入一个共享的NFS filer(注：NetApp NFS Filer)。 经常遇到需要中断服务的问题是给hadoop打补丁。 DataNod
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他