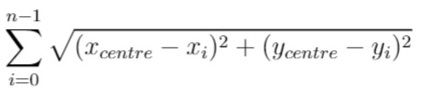leetcode第197场周赛题目及题解

leetcode第197场周赛题目及题解

第一题 leetcode 1512 好数对的数目

题目简介

给你一个整数数组 nums 。如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ，就可以认为这是一组好数  
对 。返回好数对  的数目。

示例1

输入：nums = [1,2,3,1,1,3]
输出：4
解释：有 4 组好数对，分别是 (0,3), (0,4), (3,4), (2,5) ，下标从 0 开始。

示例2

输入：nums = [1,1,1,1]
输出：6
解释：数组中的每组数字都是好数对。

数据范围

1 <= nums.length <= 100
1 <= nums[i] <= 100

题目分析

这个题目就是找数字相同的有多少对，不考虑顺序。所以我们可以首先将原数组排序，然后用双指针找出所有连续相  
等数字的个数，然后进行统计。时间复杂度O(nlogn)。

代码展示

class Solution {
public:
    int numIdenticalPairs(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int res=0;
        for(int i=0,j=0;i<nums.size();i++)
        {
            while(j<nums.size()&&nums[j]==nums[i]) j++;
            if(j-i>=2)res+=(j-i)*(j-i-1)/2;
            i=j-1;
        }
        return res;
    }
};

第二题 leetcode 1513 仅含1的子串数

题目简介

给你一个二进制字符串 s（仅由 '0' 和 '1' 组成的字符串）。
返回所有字符都为 1 的子字符串的数目。
由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

示例1

输入：s = "0110111"
输出：9
解释：共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次

示例2

输入：s = "101"
输出：2
解释：子字符串 "1" 在 s 中共出现 2 次

数据范围

s[i] == '0' 或 s[i] == '1'
1 <= s.length <= 10^5

题目分析

找出所有的含1子串进行计数即可。时间复杂度O(n)。

代码展示

class Solution {
public:
    int numSub(string s) {
        int res=0;
        int cnt=0;
        for(int i=0;i<s.size();i++)
        {
            if(s[i]=='1')
            {
                cnt++;
                res=(res+cnt)%1000000007;
            }
            else cnt=0;
        }
        return res;
    }
};

第三题 leetcode 1514 概率最大的路径

题目简介

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b]   
表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。 
指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。
如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例1

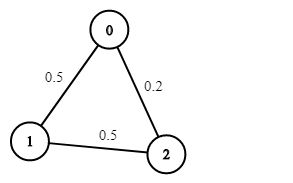
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

数据范围

2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边

题目分析

代码展示

//spfa
typedef pair<int,double> PID;

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<vector<PID>> g(n);
        for(int i=0;i<edges.size();i++)
        {
            int x=edges[i][0],y=edges[i][1];
            double c=succProb[i];
            g[x].push_back({y,c});
            g[y].push_back({x,c});
        }
        queue<int> q;
        vector<bool> st(n);
        vector<double> d(n);
        q.push(start);
        d[start]=1;
        st[start]=true;
        while(q.size())
        {
            int t=q.front();
            q.pop();
            st[t]=false;
            for(int i=0;i<g[t].size();i++)
            {
                int y=g[t][i].first;
                double w=g[t][i].second;
                if(d[y]<d[t]*w)
                {
                    d[y]=d[t]*w;
                    if(!st[y])
                    {
                        q.push(y);
                        st[y]=true;
                    }
                }
            }
        }
        return d[end];
    }
};

// dijkstra
typedef pair<int,double> PID;
typedef pair<double,int> PDI;
class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<vector<PID>> g(n);
        for(int i=0;i<edges.size();i++)
        {
            int x=edges[i][0],y=edges[i][1];
            double c=succProb[i];
            g[x].push_back({y,c});
            g[y].push_back({x,c});
        }
        priority_queue<PDI> q;
        vector<bool> st(n);
        vector<double> d(n);
        q.push({1,start});
        d[start]=1;
        while(q.size())
        {
            auto t=q.top();
            q.pop();
            double dis=t.first,id=t.second;
            if(!st[id])
            {
                st[id]=true;
                for(int i=0;i<g[id].size();i++)
                {
                    int y=g[id][i].first;
                    double w=g[id][i].second;
                    if(d[y]<dis*w)
                    {
                        d[y]=dis*w;
                        q.push({d[y],y});
                    }
                }
            }
        }
        return d[end];
    }
};

第四题 leetcode 1515 服务中心的最佳位置

题目简介

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依  
据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置，返回到所有  
客户的 欧几里得距离的最小总和 。
换句话说，请你为服务中心选址，该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值：
与真实值误差在 10^-5 之内的答案将被视作正确答案。

示例1

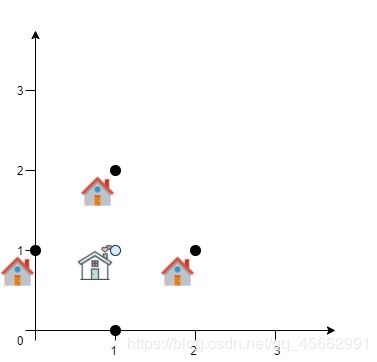
输入：positions = [[0,1],[1,0],[1,2],[2,1]]
输出：4.00000
解释：如图所示，你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置，这样一来到每个客户的距离就都是  
 1，所有距离之和为 4 ，这也是可以找到的最小值。

数据范围

1 <= positions.length <= 50
positions[i].length == 2
0 <= positions[i][0], positions[i][1] <= 100

题目分析

方法为三分套三分，具体证明可以看这里的视频讲解。

代码展示

class Solution {
public:
    vector<vector<int>> points;
    double get_sum(double x,double y)
    {
        double res=0;
        for(auto &p:points)
        {
            double a=p[0],b=p[1];
            res+=sqrt((a-x)*(a-x)+(b-y)*(b-y));
        }
        return res;
    }
    double cal(double x)
    {
        double l=0,r=100;
        while(r-l>1e-7)
        {
            double y1=l+(r-l)/3,y2=l+(r-l)/3*2;
            if(get_sum(x,y1)<=get_sum(x,y2)) r=y2;
            else l=y1;
        }
        return get_sum(x,r);
    }
    double getMinDistSum(vector<vector<int>>& positions) {
        points=positions;
        double l=0,r=100;
        while(r-l>1e-7)
        {
            double x1=l+(r-l)/3,x2=l+(r-l)/3*2;
            if(cal(x1)<=cal(x2)) r=x2;
            else l=x1;
        }
        return cal(r);
    }
};

本篇文章题目简介部分均引自leetcode网站。