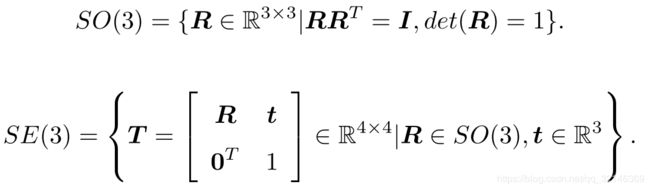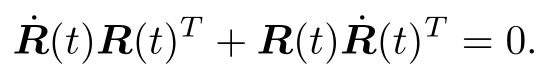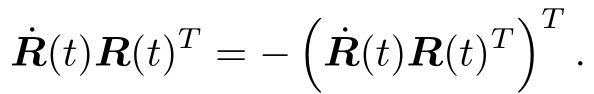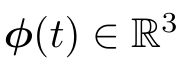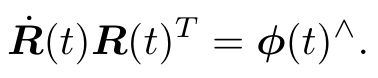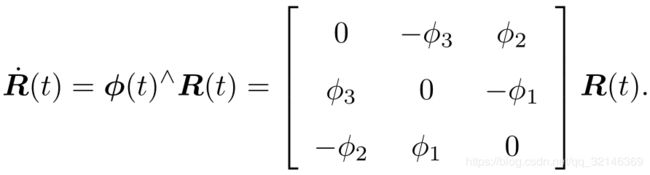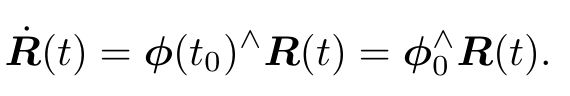- 【MotionCap】DROID-SLAM 1 :介绍及安装
等风来不如迎风去
AI入门与实战人工智能SLAHMRDROID-SLAM
DROID-SLAM:DROID-SLAM:DeepVisualSLAMforMonocularDROID-SLAM:适用于单目、立体和RGB-D相机的深度视觉SLAMStereo,andRGB-DCamerashttps://arxiv.org/abs/2108.10869DROID-SLAM:DeepVisualSLAMforMonocular,Stereo,andRGB-DCamerasfi
- 【ORB-SLAM2:三、 地图初始化】
KeyPan
ORB-SLAM2数码相机计算机视觉人工智能机器学习深度学习算法
地图初始化是视觉SLAM系统的关键步骤之一,它是整个系统运行的起点。初始化的主要任务是从输入图像数据中构建一个初始地图,为后续的相机位姿估计和场景重建提供基础。无论是单目、双目还是RGB-D相机,地图初始化的结果直接决定了系统的鲁棒性和精度。3.1为什么需要地图初始化3.1.1地图初始化的重要性定义初始参考坐标系地图初始化为SLAM系统提供了一个全局参考坐标系,使后续的位姿估计和地图扩展能够在一致
- 【视觉SLAM:六、视觉里程计Ⅰ:特征点法】
KeyPan
视觉SLAM计算机视觉人工智能机器学习数码相机算法深度学习
视觉里程计(VisualOdometry,VO)是通过处理图像序列,估计摄像头在时间上的相对位姿变化的技术。它是视觉SLAM的重要组成部分之一,主要通过提取图像中的信息(如特征点或直接像素强度)来实现相机运动估计。以下从特征点法、2D-2D对极几何、三角测量、3D-2D的PnP方法、3D-3D的ICP方法介绍视觉里程计的核心内容。特征点法特征点法是视觉里程计的经典方法,通过提取图像中的显著特征点,
- 【视觉惯性SLAM:十五、ORB-SLAM3中的IMU预积分】
KeyPan
视觉惯性SLAM计算机视觉视觉检测
15.1视觉惯性紧耦合15.1.1视觉惯性紧耦合的重要性视觉惯性紧耦合(Visual-InertialTightCoupling)在ORB-SLAM3中的作用不可替代,是实现高鲁棒性和高精度定位的核心技术。单一的视觉SLAM主要依赖于图像特征进行定位和建图,这种方法虽然能够在许多环境中获得良好的效果,但其鲁棒性容易受到动态变化、光照条件恶化以及环境特征稀缺等因素的限制。例如,昏暗场景或快速运动可能
- 视觉SLAM学习打卡【8-1】-视觉里程计·直接法
肝帝永垂不朽
#SLAM计算机视觉opencvc++
本节直接法与上节特征点法,为视觉里程计估计位姿的两大主流方法。而在引出直接法前,先介绍光流法(二者均对灰度值I做文章)。至此,前端VO总算结束了。学下来一个感受就是前几章的数学基础很重要,尤其是构建最小二乘的非线性优化(BA),几乎每种方法都有其一席之地。视觉SLAM学习打卡【8-1】-视觉里程计·直接法一、光流法(1)前提(实际中较难满足)(2)理论推导(3)附:超定方程求解二、直接法(1)理论
- 视觉SLAM十四讲学习笔记——第十讲 后端优化(2)
晒月光12138
视觉SLAM十四讲学习笔记slamubuntu
上文提到考虑全局的后端优化计算量非常大,因此在计算增量方程时,借助H矩阵的稀疏性加速运算。但是随着时间的推移,累积的相机位姿和路标数量还是会导致计算量过大,以上一节的示例代码数据为例:16张图像,共提取到22106个特征点,这些特征点共出现了83718次。对于一个20Hz更新速度,上述的数据量甚至还不到1s的内容,因此在求解大规模定位建图问题时,一定要控制BA的规模。这里主要有两种解决思路:(1)
- 视觉slam十四讲学习笔记(六)视觉里程计 1
苦瓜汤补钙
视觉SLAM十四讲笔记机器学习ubuntu
本文关注基于特征点方式的视觉里程计算法。将介绍什么是特征点,如何提取和匹配特征点,以及如何根据配对的特征点估计相机运动。目录前言一、特征点法1特征点2ORB特征FAST关键点BRIEF描述子3特征匹配二、实践:特征提取和匹配三、2D-2D:对极几何1对极约束2本质矩阵3单应矩阵四、实践:对极约束求解相机运动五、三角测量总结前言1.理解图像特征点的意义,并掌握在单幅图像中提取出特征点,及多幅图像中匹
- 视觉SLAM十四讲学习笔记——第五讲 相机与图像
晒月光12138
视觉SLAM十四讲学习笔记自动驾驶计算机视觉人工智能
这一讲主要内容就是了解摄像机的成像模型以及OpenCV的使用。1.四种坐标系坐标系基本描述世界坐标系因为摄像机和物体可以随便摆放在空间中的任何位置,所以我们必须用一个固定的坐标系来描述空间中任何物体的位置和摄像机的位置和朝向,这个基准坐标系我们称之为世界坐标系。在计算机视觉中,我们通常把世界坐标系定义为摄像机坐标系或者所观测的物体的中心。摄像机坐标系摄像机坐标系的原点是摄像机的光心,X、Y轴分别平
- 视觉slam十四讲学习笔记(四)相机与图像
苦瓜汤补钙
视觉SLAM十四讲笔记相机机器学习
理解理解针孔相机的模型、内参与径向畸变参数。理解一个空间点是如何投影到相机成像平面的。掌握OpenCV的图像存储与表达方式。学会基本的摄像头标定方法。目录前言一、相机模型1针孔相机模型2畸变单目相机的成像过程3双目相机模型4RGB-D相机模型二、图像计算机中图像的表示三、图像的存取与访问1安装OpenCV2存取与访问总结前言前面介绍了“机器人如何表示自身位姿”的问题,部分地解释了SLAM经典模型中
- ORB-SLAM3运行自制数据集进行定位教程
极客范儿
ORB-SLAM━═━═━◥MR◤━═━═━IMUORB-SLAM3
目前手上有一个特定的任务,做应急救援的视觉SLAM,目前公共数据集比较少,考虑自建数据集,从网络上爬虫火灾、地震的等手机录制的视屏,应用一些现有成熟ORB-SLAM3系统到这个数据集上看效果,然后根据效果得到一些模型改进思路。文章目录一、系统配置二、制作数据集1、脚本编写2、配置文件编写3、录制视频素材4、修改CMakeLists.txt5、编译运行一、系统配置系统版本ubuntu20.04Ope
- 视觉SLAM十四讲学习笔记(二)三维空间刚体
苦瓜汤补钙
视觉SLAM十四讲笔记计算机视觉算法
哔哩哔哩课程连接:视觉SLAM十四讲ch3_哔哩哔哩_bilibili目录一、旋转矩阵1点、向量、坐标系2坐标系间的欧氏变换3变换矩阵与齐次坐标二、实践:Eigen(1)运行报错记录与解决三、旋转向量和欧拉角1旋转向量2欧拉角四、四元数1四元数的定义2四元数的运算3用四元数表示旋转4四元数到旋转矩阵的转换五、实践:Eigen(2)useGeometryvisualizeGeometry总结前言问题
- 视觉slam十四讲学习笔记(三)李群与李代数
苦瓜汤补钙
视觉SLAM十四讲笔记人工智能学习
1.理解李群与李代数的概念,掌握SO(3),SE(3)与对应李代数的表示方式。2.理解BCH近似的意义。3.学会在李代数上的扰动模型。4.使用Sophus对李代数进行运算。目录前言一、李群李代数基础1群2李代数的引出3李代数的定义4李代数so(3)5李代数se(3)二、指数与对数映射1SO(3)上的指数映射2SE(3)上的指数映射三、李代数求导与扰动模型1BCH公式与近似形式2SO(3)李代数上的
- 视觉SLAM十四讲学习笔记(一)初识SLAM
苦瓜汤补钙
计算机视觉人工智能
目录前言一、传感器1传感器分类2相机二、经典视觉SLAM框架1视觉里程计2后端优化3回环检测4建图5SLAM系统三、SLAM问题的数学表述四、Ubuntu20.04配置SLAM十四讲前言SLAM:SimultaneousLocalizationandMapping同时定位与地图构建(建图)。搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建立环地的模型。同时储计自己的运动。视觉SLA
- 【SLAM14讲编译依赖软件源码版本方面等问题汇总】
终问鼎
自动驾驶-SLAMc++自动驾驶buglinuxubuntu
"逆转鹈鹕”0.视觉SLAM十四讲1.ch3-------Eigen32.ch4-------Sophus2.ch5-------JoinMap3.ch63.1---ceres3.2---g2o4.ch7--视觉里程计5.--ch8associate.py6.--ch9project以下是本人在学习SLAM中遇到的全部问题汇总(主要是依赖和软件方面的)。0.视觉SLAM十四讲1.ch3------
- 《视觉SLAM十四讲》第九讲前段实践中g2o实践代码报错解决方法
大二哈
在《视觉SLAM十四讲》中针对于g2o初始化部分代码是无法执行的,在高博的Git上的代码也是无法编译的,会报错:error:nomatchingfunctionforcallto‘g2o::BlockSolver>::BlockSolver(g2o::BlockSolver>::LinearSolverType*&)’定位报错的代码段如下:typedefg2o::BlockSolver>Block
- 计算机视觉中的Homography单应矩阵应用小结
CS_Zero
SLAM计算机视觉CV计算机视觉slam几何学
计算机视觉中的Homography(单应)矩阵应用小结Homography矩阵在StructurefromMotion(SfM)或三维重建、视觉SLAM的初始化过程有着重要应用,本文总结了单应矩阵出现场景与常见问题求解。文章目录计算机视觉中的Homography(单应)矩阵应用小结单应矩阵的推导单应矩阵的求解与分解位姿问题单应矩阵的推导一般地,单应模型出现的前提条件是空间点分布在同一个平面上,例外
- 【视觉SLAM十四讲学习笔记】第六讲——状态估计问题
趴抖
视觉SLAM十四讲学习笔记笔记SLAM
专栏系列文章如下:【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍【视觉SLAM十四讲学习笔记】第二讲——初识SLAM【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角【视觉SLAM十四讲学习笔记】第三讲——四元数【视觉SLAM十四讲学习笔记】第三讲——Eigen库【视觉SLAM十四讲学习笔记】第四讲——李群与李代数基础【视觉SLAM十四讲
- 【视觉SLAM十四讲学习笔记】第六讲——非线性最小二乘
趴抖
视觉SLAM十四讲学习笔记笔记SLAM
专栏系列文章如下:【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍【视觉SLAM十四讲学习笔记】第二讲——初识SLAM【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角【视觉SLAM十四讲学习笔记】第三讲——四元数【视觉SLAM十四讲学习笔记】第三讲——Eigen库【视觉SLAM十四讲学习笔记】第四讲——李群与李代数基础【视觉SLAM十四讲
- INDEMIND双目惯性模组运行实时ORB-SLAM3教程
极客范儿
ORB-SLAM━═━═━◥MR◤━═━═━ORB-SLAM3INDEMINDROSubuntu20.04imu
现在实验室视觉SLAM已经不够满足,所以需要多模态融合,正巧购入高翔博士推荐的INDEMIND双目惯性模组,根据官方例程在中使用ROS接入ORB-SLAM3,这回有SDK及ORB-SLAM3安装过程中的各种常见性问题解决方法及安装细节,与官网教程略有不同,列举所有默认安装的依赖,做以记录。文章目录实验环境一、SDK安装1、SDK下载及准备安装2、安装依赖3、然后使用git下载SDK4、准备安装SD
- 科普类(双目视觉)——快速索引
JANGHIGH
科普类无人驾驶快速索引自动驾驶
科普类(双目视觉)——快速索引科普类——双目视觉在无人驾驶汽车中的应用(一)科普类——双目视觉SLAM在无人驾驶汽车中的作用(二)科普类——双目视觉在自动驾驶中存在的问题、挑战以及解决方案(三)科普类——双目视觉系统在无人驾驶汽车中的安装位置(四)科普类——基线的设计对于系统的性能的直接影响(五)科普类——百度Apollo使用的双目系统的硬件型号(六)科普类——进行基线设计、系统测试和优化的立体视
- 科普类——双目视觉SLAM在无人驾驶汽车中的作用(二)
JANGHIGH
科普类无人驾驶汽车人工智能
科普类——双目视觉SLAM在无人驾驶汽车中的作用(二)在无人驾驶汽车中,视觉SLAM(SimultaneousLocalizationandMapping,即同时定位与地图构建)是一种关键技术,它允许车辆在未知环境中进行自我定位和地图构建。双目视觉系统在视觉SLAM中的应用起到了以下作用:精确定位:双目视觉系统通过计算两幅图像之间的视差,可以提供精确的深度信息。这些信息有助于SLAM算法更准确地估
- 【ORB-SLAM2源码梳理1】以单目mono_tum.cc为例,构建SLAM系统(含mono_tum.cc、System.cc关键代码解析)
Jay_z在造梦
ORB-SLAM2c++slamorb
文章目录前言一、进入mono_tum.cc1.导入TUM数据集图片:LoadImages()2.构建SLAM系统:System3.系统构建结束,开启跟踪线程1)一帧帧地读取对应路径下的rgb图像:2)将图像帧传入Tracking线程,开始一系列操作(关键):二、代码导图前言因为对于视觉SLAM而言,单目涉及初始化等步骤,相对于双目和RGBD较为复杂,故从单目学起。学习记录。一、进入mono_tum
- 手把手带你死磕ORBSLAM3源代码(六十四) LocalMapping.cc LocalMapping Run
安城安
数据库服务器网络运维vimlinuxc语言
目录一.前言二.代码2.1完整代码一.前言以下是对该方法功能的详细解释:mbFinished被设置为false,表示局部映射过程尚未完成。方法进入一个无限循环,这是因为在视觉SLAM中,局部映射是一个持续进行的过程,需要不断地处理新的关键帧和地图点。通过调用SetAcceptKeyFrames(false)方法,局部映射告诉追踪器(Tracker)它目前正在忙,不应该接受新的关键帧。这是为了确保局
- 视觉SLAM十四讲|【四】误差Jacobian推导
影子鱼Alexios
algorithm机器学习机器人
视觉SLAM十四讲|【四】误差Jacobian推导预积分误差递推公式ω=12((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))\omega=\frac{1}{2}((\omega_b^k+n_k^g-b_k^g)+(w_b^{k+1}+n_{k+1}^g-b_{k+1}^g))ω=21((ωbk+nkg−bkg)+(wbk+1+nk+1g−bk+1g))其中,wbkw_b^kw
- 视觉SLAM十四讲|【六】基于特征匀速模型的重投影误差计算形式
影子鱼Alexios
algorithm控制理论机器学习机器人人工智能
视觉SLAM十四讲|【六】基于特征匀速模型的重投影误差计算形式基本推导方法无时间戳延迟时,残差计算流程:世界坐标系中的第lll个地图点变换到相机坐标系下为flw=[x,y,z]Tf_l^w=[x,y,z]^Tflw=[x,y,z]T变换到相机坐标系下为flci=RcbRwbiT(flw−pwbi)+pcbf_l^{c_i}=R_{cb}R_{wb_i}^T(f_l^w-p_{wb_i})+p_{c
- 《SLAM十四讲》Ch7编译报错
Prejudices
SLAMSLAM
《SLAM十四讲》Ch7编译报错原因:视觉SLAM书上的程序使用的g2o版本比较旧了,使用的是c++11版本的g2o。而自己在编译g2o的时候编译的是最新版本的g2o,里面大量使用了c++14标准库的一些新特性,比如std::index_sequence等等。而书上的CMakeLists.txt默认使用的是c++11进行cmake编译,所以报错解决:CMakeLists.txt中更改如下:set(
- openvslam------slam解读系列
xiechaoyi123
SLAM系列slamoptimization
是什么:openvslam是日本先进工业科技研究(NationalInstituteofAdvancedIndustrialScienceandTechnology)所于2019年5月20日开源的视觉SLAM框架;github源码地址:https://github.com/xdspacelab/openvslam干什么的:先上图:通过不同类型的相机(单目,双目,RGBD,鱼眼或者全景相机)拍摄的序
- ORB_SLAM3:IMU初始化过程梳理以及自己的理解
追风筝的人~TH
ORB_SLAM3计算机视觉人工智能c++
LocalMapping线程中IMU初始化:1、为什么要进行初始化?因为无法保证世界坐标系(单目初始化参考关键帧)的Z轴正好与重力方向平行,二者有角度,计算该角度的过程就是IMU初始化的过程。2、IMU初始化过程中不断优化尺度,在单目相机的视觉SLAM中,尺度指的是场景中真实物体的物理尺寸与它在相机图像中所对应的像素距离之间的比例关系。在视觉SLAM中,尺度是一个非常重要的概念,因为它决定了相机观
- 第一个项目总结:双目测距(python代码转为c++代码,最终输出点云图,再转为ros点云图,再实现可视化)
zerogin+
c++opencv开发语言
目录1.双目成像原理2.双目测距python代码3.python代码转为c++代码(1)双目相机参数(2)立体校正(3)立体匹配4.opencv的点云图转为ros点云图1.双目成像原理摘自《视觉SLAM十四讲》2.双目测距python代码(46条消息)双目测距理论及其python实现_python双目测距_javastart的博客-CSDN博客具体过程为:双目标定-->立体校正(含消除畸变)-->
- SLAM中的二进制词袋生成过程和工作原理
深蓝学院
机器学习人工智能
长期视觉SLAM(SimultaneousLocalizationandMapping)最重要的要求之一是鲁棒的位置识别。经过一段探索期后,当长时间未观测到的区域重新观测时,标准匹配算法失效。当它们被健壮地检测到时,回环检测提供正确的数据关联以获得一致的地图。用于环路检测的相同方法可用于机器人在轨迹丢失后的重新定位,例如由于突然运动,严重闭塞或运动模糊。词袋的基本技术包括从机器人在线收集的图像中建
- Js函数返回值
_wy_
jsreturn
一、返回控制与函数结果,语法为:return 表达式;作用: 结束函数执行,返回调用函数,而且把表达式的值作为函数的结果 二、返回控制语法为:return;作用: 结束函数执行,返回调用函数,而且把undefined作为函数的结果 在大多数情况下,为事件处理函数返回false,可以防止默认的事件行为.例如,默认情况下点击一个<a>元素,页面会跳转到该元素href属性
- MySQL 的 char 与 varchar
bylijinnan
mysql
今天发现,create table 时,MySQL 4.1有时会把 char 自动转换成 varchar
测试举例:
CREATE TABLE `varcharLessThan4` (
`lastName` varchar(3)
) ;
mysql> desc varcharLessThan4;
+----------+---------+------+-
- Quartz——TriggerListener和JobListener
eksliang
TriggerListenerJobListenerquartz
转载请出自出处:http://eksliang.iteye.com/blog/2208624 一.概述
listener是一个监听器对象,用于监听scheduler中发生的事件,然后执行相应的操作;你可能已经猜到了,TriggerListeners接受与trigger相关的事件,JobListeners接受与jobs相关的事件。
二.JobListener监听器
j
- oracle层次查询
18289753290
oracle;层次查询;树查询
.oracle层次查询(connect by)
oracle的emp表中包含了一列mgr指出谁是雇员的经理,由于经理也是雇员,所以经理的信息也存储在emp表中。这样emp表就是一个自引用表,表中的mgr列是一个自引用列,它指向emp表中的empno列,mgr表示一个员工的管理者,
select empno,mgr,ename,sal from e
- 通过反射把map中的属性赋值到实体类bean对象中
酷的飞上天空
javaee泛型类型转换
使用过struts2后感觉最方便的就是这个框架能自动把表单的参数赋值到action里面的对象中
但现在主要使用Spring框架的MVC,虽然也有@ModelAttribute可以使用但是明显感觉不方便。
好吧,那就自己再造一个轮子吧。
原理都知道,就是利用反射进行字段的赋值,下面贴代码
主要类如下:
import java.lang.reflect.Field;
imp
- SAP HANA数据存储:传统硬盘的瓶颈问题
蓝儿唯美
HANA
SAPHANA平台有各种各样的应用场景,这也意味着客户的实施方法有许多种选择,关键是如何挑选最适合他们需求的实施方案。
在 《Implementing SAP HANA》这本书中,介绍了SAP平台在现实场景中的运作原理,并给出了实施建议和成功案例供参考。本系列文章节选自《Implementing SAP HANA》,介绍了行存储和列存储的各自特点,以及SAP HANA的数据存储方式如何提升空间压
- Java Socket 多线程实现文件传输
随便小屋
javasocket
高级操作系统作业,让用Socket实现文件传输,有些代码也是在网上找的,写的不好,如果大家能用就用上。
客户端类:
package edu.logic.client;
import java.io.BufferedInputStream;
import java.io.Buffered
- java初学者路径
aijuans
java
学习Java有没有什么捷径?要想学好Java,首先要知道Java的大致分类。自从Sun推出Java以来,就力图使之无所不包,所以Java发展到现在,按应用来分主要分为三大块:J2SE,J2ME和J2EE,这也就是Sun ONE(Open Net Environment)体系。J2SE就是Java2的标准版,主要用于桌面应用软件的编程;J2ME主要应用于嵌入是系统开发,如手机和PDA的编程;J2EE
- APP推广
aoyouzi
APP推广
一,免费篇
1,APP推荐类网站自主推荐
最美应用、酷安网、DEMO8、木蚂蚁发现频道等,如果产品独特新颖,还能获取最美应用的评测推荐。PS:推荐简单。只要产品有趣好玩,用户会自主分享传播。例如足迹APP在最美应用推荐一次,几天用户暴增将服务器击垮。
2,各大应用商店首发合作
老实盯着排期,多给应用市场官方负责人献殷勤。
3,论坛贴吧推广
百度知道,百度贴吧,猫扑论坛,天涯社区,豆瓣(
- JSP转发与重定向
百合不是茶
jspservletJava Webjsp转发
在servlet和jsp中我们经常需要请求,这时就需要用到转发和重定向;
转发包括;forward和include
例子;forwrad转发; 将请求装法给reg.html页面
关键代码;
req.getRequestDispatcher("reg.html
- web.xml之jsp-config
bijian1013
javaweb.xmlservletjsp-config
1.作用:主要用于设定JSP页面的相关配置。
2.常见定义:
<jsp-config>
<taglib>
<taglib-uri>URI(定义TLD文件的URI,JSP页面的tablib命令可以经由此URI获取到TLD文件)</tablib-uri>
<taglib-location>
TLD文件所在的位置
- JSF2.2 ViewScoped Using CDI
sunjing
CDIJSF 2.2ViewScoped
JSF 2.0 introduced annotation @ViewScoped; A bean annotated with this scope maintained its state as long as the user stays on the same view(reloads or navigation - no intervening views). One problem w
- 【分布式数据一致性二】Zookeeper数据读写一致性
bit1129
zookeeper
很多文档说Zookeeper是强一致性保证,事实不然。关于一致性模型请参考http://bit1129.iteye.com/blog/2155336
Zookeeper的数据同步协议
Zookeeper采用称为Quorum Based Protocol的数据同步协议。假如Zookeeper集群有N台Zookeeper服务器(N通常取奇数,3台能够满足数据可靠性同时
- Java开发笔记
白糖_
java开发
1、Map<key,value>的remove方法只能识别相同类型的key值
Map<Integer,String> map = new HashMap<Integer,String>();
map.put(1,"a");
map.put(2,"b");
map.put(3,"c"
- 图片黑色阴影
bozch
图片
.event{ padding:0; width:460px; min-width: 460px; border:0px solid #e4e4e4; height: 350px; min-heig
- 编程之美-饮料供货-动态规划
bylijinnan
动态规划
import java.util.Arrays;
import java.util.Random;
public class BeverageSupply {
/**
* 编程之美 饮料供货
* 设Opt(V’,i)表示从i到n-1种饮料中,总容量为V’的方案中,满意度之和的最大值。
* 那么递归式就应该是:Opt(V’,i)=max{ k * Hi+Op
- ajax大参数(大数据)提交性能分析
chenbowen00
WebAjax框架浏览器prototype
近期在项目中发现如下一个问题
项目中有个提交现场事件的功能,该功能主要是在web客户端保存现场数据(主要有截屏,终端日志等信息)然后提交到服务器上方便我们分析定位问题。客户在使用该功能的过程中反应点击提交后反应很慢,大概要等10到20秒的时间浏览器才能操作,期间页面不响应事件。
根据客户描述分析了下的代码流程,很简单,主要通过OCX控件截屏,在将前端的日志等文件使用OCX控件打包,在将之转换为
- [宇宙与天文]在太空采矿,在太空建造
comsci
我们在太空进行工业活动...但是不太可能把太空工业产品又运回到地面上进行加工,而一般是在哪里开采,就在哪里加工,太空的微重力环境,可能会使我们的工业产品的制造尺度非常巨大....
地球上制造的最大工业机器是超级油轮和航空母舰,再大些就会遇到困难了,但是在空间船坞中,制造的最大工业机器,可能就没
- ORACLE中CONSTRAINT的四对属性
daizj
oracleCONSTRAINT
ORACLE中CONSTRAINT的四对属性
summary:在data migrate时,某些表的约束总是困扰着我们,让我们的migratet举步维艰,如何利用约束本身的属性来处理这些问题呢?本文详细介绍了约束的四对属性: Deferrable/not deferrable, Deferred/immediate, enalbe/disable, validate/novalidate,以及如
- Gradle入门教程
dengkane
gradle
一、寻找gradle的历程
一开始的时候,我们只有一个工程,所有要用到的jar包都放到工程目录下面,时间长了,工程越来越大,使用到的jar包也越来越多,难以理解jar之间的依赖关系。再后来我们把旧的工程拆分到不同的工程里,靠ide来管理工程之间的依赖关系,各工程下的jar包依赖是杂乱的。一段时间后,我们发现用ide来管理项程很不方便,比如不方便脱离ide自动构建,于是我们写自己的ant脚本。再后
- C语言简单循环示例
dcj3sjt126com
c
# include <stdio.h>
int main(void)
{
int i;
int count = 0;
int sum = 0;
float avg;
for (i=1; i<=100; i++)
{
if (i%2==0)
{
count++;
sum += i;
}
}
avg
- presentModalViewController 的动画效果
dcj3sjt126com
controller
系统自带(四种效果):
presentModalViewController模态的动画效果设置:
[cpp]
view plain
copy
UIViewController *detailViewController = [[UIViewController al
- java 二分查找
shuizhaosi888
二分查找java二分查找
需求:在排好顺序的一串数字中,找到数字T
一般解法:从左到右扫描数据,其运行花费线性时间O(N)。然而这个算法并没有用到该表已经排序的事实。
/**
*
* @param array
* 顺序数组
* @param t
* 要查找对象
* @return
*/
public stati
- Spring Security(07)——缓存UserDetails
234390216
ehcache缓存Spring Security
Spring Security提供了一个实现了可以缓存UserDetails的UserDetailsService实现类,CachingUserDetailsService。该类的构造接收一个用于真正加载UserDetails的UserDetailsService实现类。当需要加载UserDetails时,其首先会从缓存中获取,如果缓存中没
- Dozer 深层次复制
jayluns
VOmavenpo
最近在做项目上遇到了一些小问题,因为架构在做设计的时候web前段展示用到了vo层,而在后台进行与数据库层操作的时候用到的是Po层。这样在业务层返回vo到控制层,每一次都需要从po-->转化到vo层,用到BeanUtils.copyProperties(source, target)只能复制简单的属性,因为实体类都配置了hibernate那些关联关系,所以它满足不了现在的需求,但后发现还有个很
- CSS规范整理(摘自懒人图库)
a409435341
htmlUIcss浏览器
刚没事闲着在网上瞎逛,找了一篇CSS规范整理,粗略看了一下后还蛮有一定的道理,并自问是否有这样的规范,这也是初入前端开发的人一个很好的规范吧。
一、文件规范
1、文件均归档至约定的目录中。
具体要求通过豆瓣的CSS规范进行讲解:
所有的CSS分为两大类:通用类和业务类。通用的CSS文件,放在如下目录中:
基本样式库 /css/core
- C++动态链接库创建与使用
你不认识的休道人
C++dll
一、创建动态链接库
1.新建工程test中选择”MFC [dll]”dll类型选择第二项"Regular DLL With MFC shared linked",完成
2.在test.h中添加
extern “C” 返回类型 _declspec(dllexport)函数名(参数列表);
3.在test.cpp中最后写
extern “C” 返回类型 _decls
- Android代码混淆之ProGuard
rensanning
ProGuard
Android应用的Java代码,通过反编译apk文件(dex2jar、apktool)很容易得到源代码,所以在release版本的apk中一定要混淆一下一些关键的Java源码。
ProGuard是一个开源的Java代码混淆器(obfuscation)。ADT r8开始它被默认集成到了Android SDK中。
官网:
http://proguard.sourceforge.net/
- 程序员在编程中遇到的奇葩弱智问题
tomcat_oracle
jquery编程ide
现在收集一下:
排名不分先后,按照发言顺序来的。
1、Jquery插件一个通用函数一直报错,尤其是很明显是存在的函数,很有可能就是你没有引入jquery。。。或者版本不对
2、调试半天没变化:不在同一个文件中调试。这个很可怕,我们很多时候会备份好几个项目,改完发现改错了。有个群友说的好: 在汤匙
- 解决maven-dependency-plugin (goals "copy-dependencies","unpack") is not supported
xp9802
dependency
解决办法:在plugins之前添加如下pluginManagement,二者前后顺序如下:
[html]
view plain
copy
<build>
<pluginManagement
 是一个反对称矩阵。对于任意反对称矩阵,我们能找到一个与之对应的向量。把这个运算用符号∨表示
是一个反对称矩阵。对于任意反对称矩阵,我们能找到一个与之对应的向量。把这个运算用符号∨表示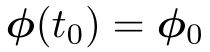 。
。