扩展欧几里德算法详解 以及模线性方程最小整数解 例: POJ -1061青蛙的约会
要彻底理解扩展欧几里德算法(递归实现)需要知道以下几个知识点:
-
欧几里德算法的原理
-
递归的回溯
-
贝祖等式
1.欧几里得算法的证明:
欧几里德算法是用来求两个数的最大公因数,其根本思想是gcd(a,b) = gcd(b,a%b
文字表达就是 a 和 b 的最大公因数 等于 b 和 a%b 的最大公因数相等, 当求解到当a%b==0时,最大公因数就是b。那么这个式子为什么成立呢?
首先我们先来回顾一下除法和取余的概念:
10个苹果,每2个装在一个盘子里,能装满几个盘子?
能装10 / 2 = 5个 ,这就是除法的含义:
把 10 以 2 为一份等分,能分几份。即 一个数 以 某个值 为一份 等分 ,能分几份
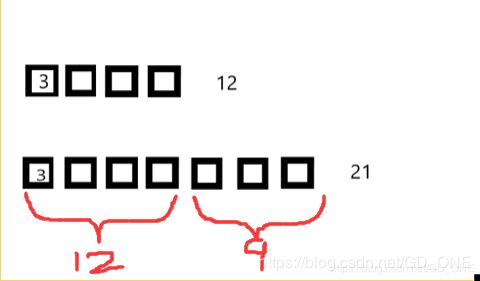
以 12 和 21 为例 ,两数的最大公因数为3,则 12 可以看做是 4 个 3 ,21 可以看做 7 个 3 。如图:
21 / 12 根据除法的定义 就是 将21 以 12 为一份等分,能分一份,余9。因为21和12都是由3组成的集合,所以从21中划走12后 剩下的数 还是由3的集合构成 所以我们可以得到 :不互质的两个数,一个数对另一个数取余后,最大公因数不变。 如图:
即 gcd(a,b)= gcd(b,a%b);
接下来我们要通过欧几里得算法求解x 和 y;
int gcd(a,b){
if(b==0) // 当 b==0, a==gcd(a,b)
return a;
return gcd(b,a%b);
}欧几里得算法的递归出口是 b == 0; a == gcd(a,b) ; 将 此时的a,b代入 a*x + b*y = gcb(a,b)中得: gcb(a,b)*x = gcb(a,b) 显然 x = 1; y为任意值,为了方便计算,设y=0;
所以 x = 1,y = 0,是当a==gcb(a,b) ,b==0时的解,我们可以利用这个x和y求解原式中x和y 的值,因为 gcd(a,b)= gcd( b,a%b ) ; 所以 a*x + b*y = b * x1 + (a%b) * y1 (1) 又因为 a%b = a - (a/b)*b (2)
将(2)式带入(1)式后得 A * X + B * Y = B*X1 + (A- (A/B) * B) * Y1
A*X + B*Y = B*X1 +A*Y1 - ((A/B) *B) *Y1
A*X + B* Y = A* Y1 + B(X1-(A/B)*Y1)
所以 X = Y1 Y = X1-(A/B) *Y1
得到了 a*x + b *y = b*x1 + a%b * y1 中 x ,y 和 x1 , y1的关系之后我们就能通过这个式子从递归出口向上回溯,最终得到a*x+b*y = gcd(a,b) 中的 x 和 y
上面已经说过函数执行至递归出口时 x0 = 1,y0 = 0; 那么递归的上一层中的 x = y0 y =x0-(A/B)*y0
为了更直观的解释,直接模拟一遍 以 21 和 12 为例
首先调用 gcd(a,b)函数
a=21 b=12 b != 0
a=12 b=21%12=9 b!=0
a=9 b= 12%9 =3 b!=0
a=3 b = 9%3 ==0 b == 0 gcd(a,b)== a ==3; 此时 令 x = 1 , y = 0 即
(a=3 ,b=0) 3 * 1 + 0 * 0 = 3 这是递归的最后一层 上一层的 a=9 , b=3 所以我们通过求出的x,y和x1 ,y1的关系可得:
(a=9, b=3) x = 0 , y = 1 - ( 9/3 * 0) =1 (X = Y1 Y = X1-(A/B) *Y1 ) X,Y 是上一层函数,X1,Y1是下一层函数
(a=12,b=9) x = 1 , y = 0 - (12/9 * 1)= -1
(a=21,b=12) x = -1 y = 1 - (21/12 * -1) = 2 最终求得 x = -1 , y = 2 21*(-1)+ 12*2 = 3 答案正确
以上就是扩展欧几里得算法的全部内容, 以下是代码实现:
ll exgcd(ll a, ll b, ll &x, ll &y){ // 防止溢出变量全部设为long long
if(b==0) {
x = 1;
y = 0;
return a;
}
exgcd(b,a%b,y,x); // 将 x y交换位置 等同于 x = y1
y = y - a/b*x; //等号右边的x,y是下层函数的x,y
}例题: POJ -1061青蛙的约会
题目大意: 两只青蛙在同一个圈里,它们需要去同一个位置,但它们两个每次只能跳固定的距离,且同时跳,给出两只青蛙的初始位置x,y,以及它们每次跳的距离m,n 和圈子的总长度L 求它们最少跳多少次可以跳到同一位置。设i为跳的次数很容易得出:
(x + i*m )% L = (y + i*n)%L (%L之后就是青蛙在圈子中的位置了)
所以转化之后得 x + i*m = y + i*n + L*k 或者 x + i*m + L*k= y + i*n(K是圈数) (也就是追及相遇问题,一个总要比另一个多跳几整圈,操场上跑步,都只能顺时针跑,你前面的人想要追上你只能比你多跑一圈)
我们可以将上面的式子化为 a*x + b*y = c 的格式 这样我们就可以通过扩展欧几里算法得到x和y
将 x + i*m = y + i*n + L*k 转化为: x - y = i*(n-m) + L*k x,y,n,m,L 都是已知量,求出 i 就好了
所以 令 a = n-m b = L c = x - y 得到 a * i + b * k = c 如果 i 有整数解的话, 那么 c 一定是gcd(a,b)的整倍数
即 c % gcd(a,b)==0 否则 无整数解,所以 i就是x,k就是y , 最后求出x后,再将x乘以 c/gcd(a,b) 就求出 a*x+b*y=c中的 x 了,但还有一个小问题
这个题就是标准的扩展欧几里得模板题,唯一需要额外处理的地方就是要得到最小正整数解,因为使用扩展欧几里得算法得到的只是一个特解 就比如说
21*(-1) + 12 * 2 等于 3 21*3 + 12*(-5)也等于 3 所以-1,2 和 3,-5 是两组不同的解
我们需要的是一个最小的正整数解 因为青蛙跳的次数不可能是负的,如果是负数,可以理解为倒着跳
比如 两只青蛙的位置分别是 1 , 2 它们分别跳 3, 4 圈大小为 5 则它们向后跳一次之后 第一只青蛙的位置变为3第二只青蛙的位置也变为3 所以如果不对x进行处理的话 求出的答案就是 -1
那么我们如何得到最小正整数解? 它们最多跳5次以后,就会回到初始的位置,在这之前,如果他们还没有相遇,那么它们就永远不会相遇,所以它们跳的次数的范围就是 【1,5】 这个5怎么求呢
我们设 a * x1 + b * y1 = c (1) 和 a * x2 + b * y2 =c (2) 中 x1,y1 x2,y2 是两组特解我们可以求出x,y的通解式
将(1)、(2)结合 得到
a * x1 + b * y1 = a * x2 + b * y2
a(x1-x2)= b (y2-y1)
a/gcd(a,b)* (x1-x2) = b/gcd(a,b) * (y2 - y1) // 两边同时除以 gcd(a,b),使 a和b互质
则 a' * (x1-x2) = b' * (y2-y1) 因为此时a' 和 b' 互质 所以要想让等式成立 则 (x1-x2 )是b'的整倍数,(y2-y1)是a'的整倍数 所以 x1 - x2 = b' * k (k是1,2,3,4,5....) 所以 x1 = x2 +b' * k 就是方程a*x+b*y = c 中 关于x的通解式,我们只需要知道一个特解就可以求出其他所有特解,进而得到符合条件的特解 当我们取最小正整数解时,令k=1,(k最小为1) 所以满足条件的最小正整数解的取值范围是【1,b'】 b' = b/gcd(a,b) 我们通过取余的方式可以让 x 的值在【1,b/gcd(a,b)】之间
所以 x = (x%b'+b')%b' 或者 x = x%b; if(x<0) x+=b;
代码:
#include
#include
#include
#include
#include
#define ll long long
using namespace std;
ll gcd(ll a, ll b){
if(b==0) return a;
return gcd(b,a%b);
}
ll exgcd(ll a, ll b, ll &x, ll &y){
if(b==0) {
x = 1;
y = 0;
return a;
}
exgcd(b,a%b,y,x);
y = y - a/b*x;
}
int main()
{
long long x,y,m,n,L,t,p,a,b,c,d;
cin>>x>>y>>m>>n>>L;
a = n-m;b = L; c = x-y; // 转化为 a*x + b*y = c
t = gcd(a,b);
if(c%t!=0) {
cout<<"Impossible";
return 0;
}
exgcd(a,b,x,y);
b = b/t;
x = x*(c/t); // 由a*x1 + b*y1 = gcd(a,b)中的x1得到 a*x1 + b*y1 = c 中的x1
x=(x%b+b)%b; // 由于x可能为负数,而我们需要得到一个最小的正整数解 所以需要对 b/gcd(a,b)
cout<