Educational Codeforces Round 87 (Rated for Div. 2)

A.Alarm Clock

题目地址

A.Alarm Clock

题意简述

P某需要睡觉a分钟,他只有听到闹钟才会起床,他先睡,他所设定的第一个闹钟将会在b分钟后响起,然后他将闹钟重置,设定为c分钟后响,然后需要花费d分钟才能入睡

题解

• 如果b≥a第一次睡就满足了a分钟了
• 那如果没有呢？就需要考虑c和d了，画个图来
  AB段是你需要睡的时间，CD段是你第一次睡的b分钟，闹钟c分钟后响，花费d分钟入睡
  我们先假设c≥d，也就DE段的时间为 c-d
  你需要睡cnt段DE使得总睡觉时间大于等于AB
  如何确保一定是大于等于的呢我们可以 AB段再加一个 DE段-1，然后计算需要多少段

LL cnt = (a - b + (c - d) - 1) / (c - d);

代码

int main(){
	int t;
	for(RD(t); t; t--){
		LL a, b, c, d; RDD(a, b);RDD(c, d);
		if (b >= a) OT(b);
		else{
			if (c <= d){
				OT(-1);
			}
			else{
				LL las = a - b;
				LL cnt = (las + (c - d) - 1) / (c - d);
				OT(b + cnt * c);
			}
		}
	}
}

B.Ternary String

题目地址

B.Ternary String

题意简述

给你一段序列，里面只包含’1’‘2’'3’字符，要求你求解包含这三个字符的最短连续子列

题解

分别记录这三个字符的最新位置，记录长度，并不断更新，确保最短

代码

int main(){
    int t;RD(t);
    while(t--){
        string s;
        cin >> s;
        int o = -1, t = -1, th = -1;
        int len = maxn;
        for(int i = 0;i < s.size(); i++){
            if (s[i] == '1') o = i;
            else if (s[i] == '2') t = i;
            else if (s[i] == '3') th = i;
            if (o != -1 && t != -1 && th != -1)
            len = min(max(o, t, th) - min(o, t, th) + 1, len);
        }
        if(len == maxn) cout << "0" << '\n';
        else cout << len << '\n';
    }
}

C1.Simple Polygon Embedding

题目地址

C1.Simple Polygon Embedding

题目简述

求解正2*n边型的最小外接正方形（n为偶数）

题解

由于n是偶数，所以在正2n边形中当中是会存在一个对称的情况
拿正2*4边形举个例子，你会发现我们EF和AB是平行的,同理GH//DC
这几个边延长便是我们的外接正方形了，由于对称性，所以可以旋转，但是结果都一样

如何求解呢，做个EF的中垂线，将角度设置为α

• 设圆心为o，其余点如图所示
• 设∠FOE=α，已知EF=1
• 即FJ/OJ=tan(α/2)
• OJ = FJ / tan(α/2)
• ans = 2 * OJ = 2 * FJ / tan(α/2)
• 已知J是中点 FJ = 1/2
• ans = 1 / tan(α/2)

角度转弧度-sin函数的使用

我们需要把角度转化为弧度才能在math库的sin函数中使用

公式： rad = α * PI / 180

代码

int main(){
    //cout << PI << '/n';
    int t;
    for(RD(t); t; t--){
        int n; RD(n);
        DB xt = 360 / (DB)(2 * n) / 2;
        DB rad = xt * (PI / 180);
        DB ans = 1 / tan(rad);
        printf("%.10f\n", ans);
    }
}

C2.Not So Simple Polygon Embedding

题目地址

C2.Not So Simple Polygon Embedding

题意简述

求解正2*n边型的最小外接正方形（n为奇数）

题解

与C1的差别就是差在n为奇数这一点上面，对于原先存在的对称行就需要重新考虑了。
奇数的情况我们换个方法，不如先把外接的正方形先画出来
然后分角度（我们就以n最小的时候为例进行画图n=3）

1. 画外接正方形

2. 分角度，由于是n=3，所以分成2n个角，于是我们可以得到每个角的度数α=360/(2n)

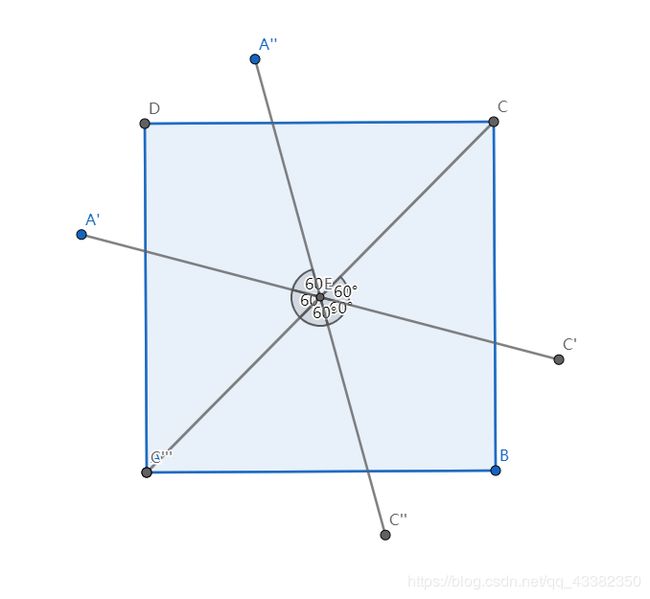
3.画圆求解正2n边形剩下的点，由于我们已经设定好了，外接正方形，所以正2n边边形必然不能超过正方形的，这也就是为什么圆的半径我们选择的是OJ而不是OC（圆心为O）

4.连接各点，现在我们很清楚，实际上我们要求的就是DF+FC

代码

int main(){
    int _;
    for(scanf("%d", &_); _;_--){
        int n; RD(n);
        printf("%.10f\n", cos(PI/(4*n))/sin(PI/(2*n)));
    }
}

D.Multiset

题目地址

D. Multiset

题意简述

给你一段长度为$n$的序列$a1,a2,a3...an$,对序列进行$q$次操作，分别为$k1,k2,k3...kn$，

• 如果$1\le ki\le n$的时候，进行插入操作，将$ki$插入到集合（multiset）中
• 如果$ki<0$的时候,则进行删除操作，将第|ki|位置的值从集合当中删除

题解

存在两种解法

1.编写数据结构，模拟解决问题,

• 树状数组
• 线段树

树状数组能解决的问题，线段树都能解决，但是树状数组的代码量小，好写，我对线段树的代码进行了测试，个人认为本题是不太适合线段树的，如果不加上快读的话，代码是会TLE在第五点

我们只需要找到一个属于集合的数字。
例如，让我们找到最小的元素。我们可以通过二分搜索来做到这一点，如下所示：让我们为给定元素编写一个函数X，告诉元素数不大于 X在生成的多集中。要实现它，请使用所有元素≤ X 难以区分，所有要素 > x 也是无法区分的，因此只需两个计数器即可维护多集。

好的，此功能有什么帮助？所得多重集中的最小值为最小值X 这样该函数将为其返回非零值，并且由于该函数是单调的，因此我们可以使用二进制搜索找到答案。

//线段树
const int maxn = 1e6 + 5;
int sumt[maxn<<2];
#define lson p<<1
#define rson p<<1|1

void ins(int p,int l,int r,int k)
{
    if(l == r) { sumt[p]++; return ;}
    int mid = l + r >> 1;
    if(k <= mid)
        ins(lson, l, mid, k);
    else
        ins(rson, mid + 1, r, k);
    sumt[p] = sumt[lson] + sumt[rson];
}

void del(int p, int l, int r, int k){
    if (l == r) {
        if (k <= sumt[p]) sumt[p]--; 
        return ;
    }
    int mid = l + r >> 1;
    if (sumt[lson] >= k) del(lson, l, mid, k);
    else del(rson, mid + 1, r, k - sumt[lson]);
    sumt[p] = sumt[lson] + sumt[rson];
}
int flag = 0;
void query(int p, int l, int r){
    if (l == r){
        if (sumt[p]) { flag = l; }
        return ;
    }
    int mid = l + r >> 1;
    query(lson, l, mid);
    query(rson, mid + 1, r);
}


int main(){
    int n, q, x; RD(n, q);
    for(int i = 1; i <= n; i++){
        RD(x); ins(1, 1, n, x);
    }
    for(int que = 1; que <= q; que++){
        RD(x);
        if (x > 0) ins(1, 1, n, x);
        else { del(1, 1, n, abs(x));}
    }
    query(1, 1, n);
    if (sumt[1]!=0) cout << flag << '\n';
    else cout << 0 << '\n';
}

//树状数组
const int maxn = 1e6+60;
int t[maxn];
struct Bit
{
    void ins(int x, int v) {
        for(; x < maxn; x += x&-x) t[x] += v;
    }
    int query(int x) {
        LL res = 0;
        for(; x; x -= x&-x) res += t[x];
        return res;
    }
    void erase(int k) {
        int now = 0;
        for(int i = 19; i > 0; --i){
            if (t[now|(1<<i)] < k){
                k -= t[now | (1<<i)];
                now |= 1 << i;
            }
        }
        if (t[now|1] < k) ins(now+2, -1);
        else ins(now+1, -1);
    }
} bit;
int main(){
    int n, q; RD(n, q);
    FOR_1(i, 1, n){
        int x; scanf("%d", &x); bit.ins(x, 1);
    }
    FOR_1(ca, 1, q){
        int k; scanf("%d", &k);
        if(k > 0) bit.ins(k, 1);
        else{
            bit.erase(-k);
        }
    }
    if(!bit.query(n)){
        cout << 0 << '\n';
    }
    else{
        FOR_1(i, 1, n){
            if(bit.query(i)){
                cout << i << '\n';
                return 0;
            }
        }
    }
}

E.Graph Coloring

F.Summoning Minions

G.Find a Gift