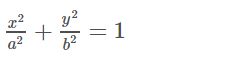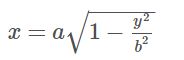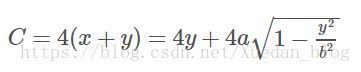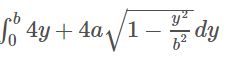2018杭电多校第六场
A - oval-and-rectangle
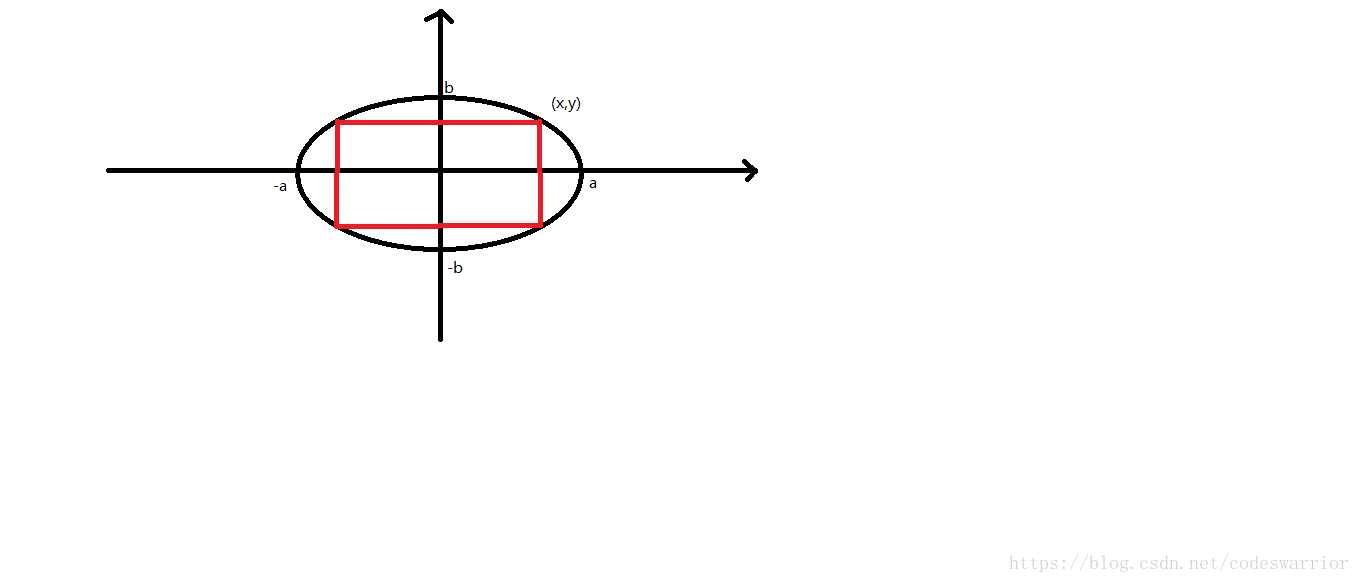
Patrick Star find an oval.
The half of longer axes is on the x-axis with length aa.
The half of shorter axes is on the y-axis with length bb.
Patrick Star plan to choose a real number cc randomly from [0,b][0,b], after that, Patrick Star will get a rectangle :
1. The four vertexes of it are on the outline of the oval.
2. The two sides of it parallel to coordinate axis.
3. One of its side is y=cy=c.
Patrick Star want to know the expectations of the rectangle's perimeter.
Input
The first line contain a integer TT (no morn than 10), the following is TT test case, for each test case : Output For each test case output one line denotes the expectations of the rectangle's perimeter . Sample Input Sample Output 题意: 求椭圆内接矩形的周长的期望 分析: 就是让求均值,把所有可能周长加起来除去变化范围即可 我们知道椭圆的公式为 这样我们知道y的变化范围是[0,b],并且我们可以求出x用y表示 因此可以得到周长公式 因为我们要求所有可能周长之和 因此实际上就是求周长的离散和即求周长公式的积分 因此我们实际上要求 因此周长和为2b^2+πab,因为变化范围是0-b 所以再除以b便是期望 所以最终只需求一个式子 2b+πa 因为题目要求保留6位小数,并且后面的全部舍去,因此为了防止%.6f造成四舍五入,因此给答案-0.0000005 代码: "The Werewolves" is a popular card game among young people.In the basic game, there are 2 different groups: the werewolves and the villagers. Input The first line of the input gives the number of test cases T.Then T test cases follow. Output For each test case,print the number of type-1 players and the number of type-2 players in one line, separated by white space. Sample Input Sample Output 题意:狼人杀游戏中,农民只能说真话,狼人可以说真话,也可以说假话,每个人给一个描述,描述另一个人是农民还是狼人,描绘的人不能是本人,问一定是农民的或一定是狼人的有多少人。 思路:因为说真话的不一定都是农民,全部都是狼人的时候也一定成立,因为狼人真话假话都可以,所以没有人一定是农民。接下来判断谁一定是狼人。 给一个场上出的样例,1说2是农民,2说1是狼人。这样的话,可以判断出1一定是狼人,因为若1是农民,讲真话,2也是农民,讲真话,1是狼人,矛盾了。 再者说,1说2是农民,2说3是农民,3说4是农民,4说1是狼人,那么1一定是狼人,证明同上。 于是我们可以给出一个推广,如果你被一个人认定是狼人,并且这个人还是你认定的农民,或者是被你间接认定的农民,那么,你一定是狼 再者,如果判断出我是狼人,那么说我是农民的人也一定是狼人。 因此,到这里这个题就可以写了。 我们使用并查集来写,刚开始我们只连接进去农民边,记录出来狼人边,最后加进去狼人边,如果狼人边的两端在同一个并查集内,则会产生狼人,首先被认定的人是狼人,其次,指向我的人是狼人,代码中v数组记录是都有谁指向我是农民,fa[]记录的是我指向的下一个人,Q用来寻找指向我是农民的人。如果狼人边的两端在不同的并查集,可以忽略不管,为什么呢,因为咱们假如x认定y是狼人,但是y在另一个并查集中,此时咱们想如果只有y是狼人,此时x整个并查集中时农民,y并查集中有狼人,这样式成立的,但是如果x并查集中是狼人,y并查集中时农民,答案也是成立的,因此这种情况下,没有一定的狼人 代码如下: 原文:http://www.cnblogs.com/Flower-Z/p/9447450.html There is a slope on the 2D plane. The lowest point of the slope is at the origin. There is a small ball falling down above the slope. Your task is to find how many times the ball has been bounced on the slope. Input There are multiple test cases. The first line of input contains an integer T (1 ≤≤ T ≤≤ 100), indicating the number of test cases. Output Output the answer. Sample Input Sample Output 思路:物理题 ,将运动分解为在斜面上的匀加速直线运动即可 代码: 原文:https://blog.csdn.net/qq_40911499/article/details/81539495
Each line contains contains two integer a, b (0
You should keep exactly 6 decimal digits and ignore the remain decimal digits.
It is guaranted that the 7-th decimal digit of answer wont be 0 or 9.1
2 18.283185#include J - Werewolf
Each player will debate a player they think is a werewolf or not.
Their words are like "Player x is a werewolf." or "Player x is a villager.".
What we know is :
1. Villager won't lie.
2. Werewolf may lie.
Of cause we only consider those situations which obey the two rules above.
It is guaranteed that input data exist at least one situation which obey the two rules above.
Now we can judge every player into 3 types :
1. A player which can only be villager among all situations,
2. A player which can only be werewolf among all situations.
3. A player which can be villager among some situations, while can be werewolf in others situations.
You just need to print out the number of type-1 players and the number of type-2 players.
No player will talk about himself.
The first line of each test case contains an integer N,indicating the number of players.
Then follows N lines,i-th line contains an integer x and a string S,indicating the i-th players tell you,"Player x is a S."
limits:
1≤T≤101≤T≤10
1≤N≤100,0001≤N≤100,000
1≤x≤N1≤x≤N
S∈S∈ {"villager"."werewolf"}1
2
2 werewolf
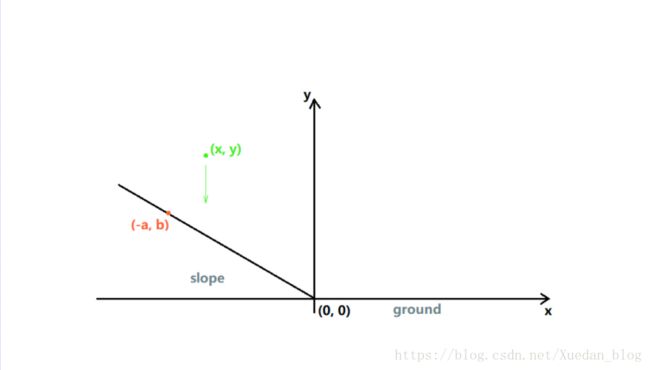
1 werewolf0 0#include L - Pinball
It's guarantee that the ball will not reach the slope or ground or Y-axis with a distance of less than 1 from the origin. And the ball is elastic collision without energy loss. Gravity acceleration g=9.8m/s^2
The first line of each test case contains four integers a, b, x, y (1 ≤≤ a, b, -x, y ≤≤ 100), indicate that the slope will pass through the point(-a, b), the initial position of the ball is (x, y).
It's guarantee that the answer will not exceed 50.1
5 1 -5 32#include