数学建模集成电路布线拥堵问题
集成电路脚标拥堵问题
集成电路通道布线中脚标拥堵问题
集成电路是利用半导体技术把电子元件集成在一起的具有特定功能的电路， 已广泛应用于生产生活的方方面面。随着技术的发展，集成电路内部的元器件数 目已达到十亿级别，需要借助专用计算机软件才能完成电路设计与实现，该类软件统称为电子设计自动化（Electronic Design Automation, EDA）工具。
集成电路设计由多个阶段组成，其中一个重要阶段称为“物理设计”，先将器件摆放在合适的位置，然后用金属线连接器件实现连接关系。其中，后者称为“布线”，它是 EDA 工具需要解决的重要问题。简单而言，假设可用区域由 m*n个方格组成，金属线允许沿着直线或直角（方格）放置，连接指定的方格（引脚）而不引起断路或短路，该过程称为“布线”。由于金属线引入的寄生电阻会影响 电路性能，所以需要最小化布线长度。本题重点考虑 “布线”问题中的一个特
例：“通道布线”。“通道”是指一个横向的布线区域，此区域的顶部和底部分布着需要连接的方格，需用金属线将相应的引脚连通起来。
（1）假设采用一层金属布线，那么已经布线的方格被锁定，不允许其它线路穿过，否则会形成短路。图 1 所示为采用一层金属的通道布线例子，布线空间为 ，空间上下沿的数字分别对应方格的引脚编号，编号相同的引脚需要连接起来。由于空间限制，角标拥堵导致无解，是布线无解的原因之一。请针对 一层金属的“通道布线”问题完成建模和求解，给出角标拥堵导致无解的条件和两三个例子。
（2）引脚标号不变的条件下，将 替换 （等于5或6或者更大）看是否有解。
（3）可以观察得到，有些测例无法采用一层金属完成布线。实际中，集成电路会采用多个金属层，不同的金属层处在不同的高度，相邻层之间需要用通孔连通，这样不同金属层可共用一个方格而不引起短路。图 2 所示为芯片的剖面图，其中网状填充为金属层，点状填充为通孔。图 3 所示为一个用两层金属的布线示例，其中蓝色为下层金属，黄色为上层金属，红色为通孔。
但是一个通孔的电阻等于 5 个方格的导线，请使用2 层金属对“通道布线”对 的脚标拥堵无法求解的问题，采用多层布局重新建模和求解，最小电阻和问题2最小电阻进行对比。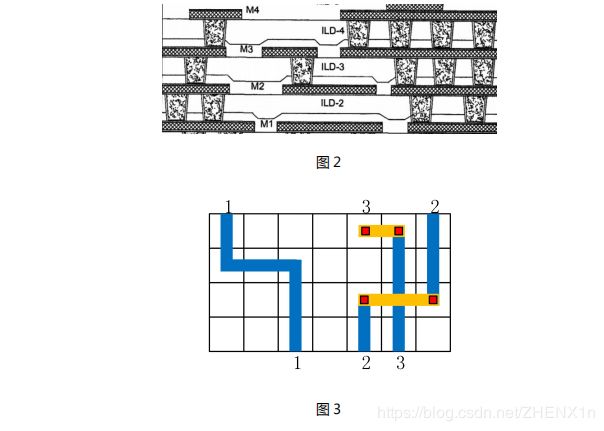
注
符号 意义
N 布线区域的宽度
K 总的引脚对数
i 第i对引脚
A_i 第i对引脚的上引脚坐标
B_i 第i对引脚的下引脚坐标
- 假设上引脚坐标从左至右按顺序编号
假设两层金属版无差异*
问题1和问题 2
启发思路我们使用A*算法
详细Python代码和解释请看这个大佬的帖子
https://blog.csdn.net/Python_Matlab/article/details/106469362
看了上面的帖子代码，你可能会理解是否有无解跟脚标顺序存在关联，不存在长 宽的关系，所以检验有无解也就是检验上下脚标顺序是否按顺序排列。
如果你不明白为什么布线拥堵是和脚标有关系 建议作图去理解~ *
0-1规划思路
我们对有解情况进行求最小布线距离。
对布线的区域赋值为1
未布线的区域赋值为0
那
$d=sum（y)=｛x=1｝ y∈（m,n）
｛x=0｝
$
方法二
是否有解采取同样的解决方法
而对于有解的距离计算采用曼哈顿距离公式进行推演
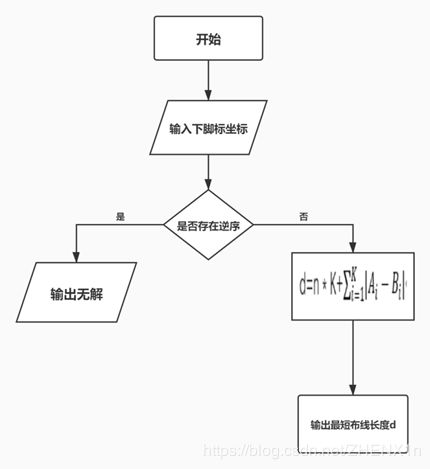
方法二的Matlab代码
1. clc;clear
2. Ai = [1 4 7 8 10 12 14 ]; %输入上脚标坐标
3. Bi = [1 2 8 5 13 11 15 ]; %输入下脚标坐标
4. a = sort(Bi); %对矩阵进行升序排序
5. n=input('请输入n的数值'); %输入宽度
6. l=input('请输入l的数值'); %输入长度
7. K = sum(sum(Bi~=0)); %K为Bi中非零元素数
8. kuandu=['宽度',num2str(n)];
9. disp(kuandu)
10. changdu=['长度',num2str(l)];
11. disp(changdu)
12. duishu=['脚标对数',num2str(K)];
13. disp(duishu)
14. shangjiaobiao=['上引脚坐标',num2str(Ai)];
15. disp(shangjiaobiao)
16. xiajiaobiao=['下引脚坐标',num2str(Bi)];
17. disp(xiajiaobiao)
18. if a==Bi %如果排序矩阵跟原矩阵相同
19. i = sym('i'); %定义i
20. ANS=abs(Ai-Bi);
21. ANS1=sum(ANS);
22. ANS2=n*K;
23. d=ANS2+ANS1;
24. Rmin=['最短布线长度',num2str(d)];
25. disp(Rmin)
26. else
27. msgbox("无解") %输出无解
28. end
问题3
对于问题3的双层解决问题
决定使第一层布线数在不拥堵的情况下达到最大，并且将剩余的布线放置到第二层，也就是将双层布线问题转化成两个一层布线问题，对于第二层脚标拥堵沿用第一问的解决方法，若第二层布线拥堵，则说明该情况在双层布线中无解。
如何使得第一层布线在不拥堵的情况下还能达到最大呢？
让第一层的引脚对数达到顺序排列最大，将剩余脚标对放置到第二层。
对于如何筛选脚标对数则分别使用了贪婪算法和二分排序法进行筛选。
贪婪算法Python代码如下
1. arrayLen = int(input()) #数组长度
2.
3.
4. list = [] #数组1
5. list2 = [] #数组2
6.
7. Temporaryarray1 = [] #暂存
8. Temporaryarray2 = []
9.
10. end_list = -1
11.
12. list = input().split()
13. list2 = input().split()
14.
15.
16. for i in range(arrayLen):
17. list[i] = int(list[i])
18. list2[i] = int(list2[i]) #将字符变为数字
19.
20.
21. for i in range(arrayLen-1):
22. if(list[end_list-1]>list[end_list]):
23. Temporaryarray1.append(list.pop(end_list-1))
24. Temporaryarray2.append(list2.pop(end_list-1))
25. else:
26. end_list = end_list -1
27. print(list)
28. print(list2)
29.
30. print()
31. print(Temporaryarray1[::-1])
32. print(Temporaryarray2[::-1])
二分排序法Matlab代码如下
1. function [s1,s2] = erfenpaixu(data)
2. % data=[100 2 6 9 5 7 8 13 11 12];
3. chang=length(data);
4. for i=1:chang
5. route(i)=0;
6. end
7. len=[];
8.
9. max_len=0;
10. len(1)=1;
11. for i=2:length(data)
12. len(i)=1;
13. route(route>=0)=0;
14. for j=1:i-1
15. if(data(j) < data(i) && (len(j) + 1) > len(i))
16. len(i) = len(j) + 1;
17. end
18. end
19. if(len(i) > max_len)
20. % s1_temp=[s1_temp data(j)];
21. max_len = len(i);
22. end
23.
24. end
25. max_len;
26.
27. max_select=max(len);
28. s1=[];
29. s2=[];
30. for i=1:max_select
31.
32. ind=find(len == i);
33. temp=min(data(ind));
34. s1=[s1,temp];
35.
36. end
37.
38. for i=1:length(data)
39. if ~ismember(data(i),s1)
40. s2=[s2,data(i)];
41. end
42. end
43.
44. s1; %第一层下脚标
45. s2; %第二层下脚标
46. %利用二分排序法进行筛选数据
data=[具体数值] 控制台输入
如果需要调用筛选后的数据控制台输入
[s1,s2]=erfenpaixu(data) %调用指令***
缺陷问题
对于以上问题的解决存在某种不具有实际意义的脚标排序情况
如 在4*7的布线空间中
上脚标 2 3 4 5 6
下脚标 6 7 8 9 10
虽然其也是按照顺序排列 但是其依然无解
其中Ai为上引脚坐标 n为宽度 Bi为下引脚坐标
也就是说如果符合该公式其布线依然拥堵，题目依然无解。
当然这个公式只是一种数学猜想，希望读者们自己进行数据检验并提出改进空间