杜教筛学习日记
文章目录
- 前置知识
- 杜教筛上:莫比乌斯函数求和
- 杜教筛上:欧拉函数求和
- 杜教筛上:小结
- 杜教筛下:前置:迪利克雷卷积
- 杜教筛下:求 ∑ i = 1 n ϕ ( i ) × i \sum_{i=1}^{n}\phi(i)\times i ∑i=1nϕ(i)×i
- 杜教筛下:一般方法
- P4213 【模板】杜教筛(Sum)
- 求 ∑ i = 1 n μ ∗ μ ( i ) \sum_{i=1}^n\mu*\mu(i) ∑i=1nμ∗μ(i)的值
- 题目
参考博客: jk_chen_acmer
前置知识
莫比乌斯反演学习日记
∑ d ∣ n μ ( d ) = [ n = 1 ] \sum_{d|n} \mu(d) = [n = 1] ∑d∣nμ(d)=[n=1]
∑ d ∣ n ϕ ( d ) = n \sum_{d|n}\phi(d) = n ∑d∣nϕ(d)=n
ϕ ( n ) = ∑ d ∣ n μ ( d ) n d \phi(n) = \sum_{d|n} \mu(d)\frac{n}{d} ϕ(n)=∑d∣nμ(d)dn ( 容 斥 过 程 ) (容斥过程) (容斥过程)
∑ d ∣ g c d ( i , j ) μ ( d ) = [ g c d ( i , j ) = 1 ] − C \sum_{d|gcd(i,j)} \mu(d) = [gcd(i,j) = 1]\;-C ∑d∣gcd(i,j)μ(d)=[gcd(i,j)=1]−C
F ( n ) = ∑ d ∣ n f ( d ) = > f ( n ) = ∑ d ∣ n u ( d ) F ( ⌊ n d ⌋ ) − B F(n)=\sum_{d|n}f(d) => f(n)=\sum_{d|n}u(d)F(⌊\frac{n}{d}⌋)\;-B F(n)=∑d∣nf(d)=>f(n)=∑d∣nu(d)F(⌊dn⌋)−B
F ( n ) = ∑ n ∣ d f ( d ) = > f ( n ) = ∑ n ∣ d u ( d n ) F ( d ) − A F(n)=\sum_{n|d}f(d) => f(n)=\sum_{n|d}u(\frac{d}{n})F(d)\;-A F(n)=∑n∣df(d)=>f(n)=∑n∣du(nd)F(d)−A
∑ i = 1 n ∑ d ∣ i f ( d ) = ∑ d = 1 n ∑ i = 1 n d f ( i ) \sum_{i=1}^{n}\sum_{d|i}f(d)=\sum_{d=1}^{n}\sum_{i=1}^{\frac{n}{d}}f(i) ∑i=1n∑d∣if(d)=∑d=1n∑i=1dnf(i)
积性函数知识点一点简单的性质,更多相关知识访问 g o o g l e google google。
杜教筛一般用于求积性函数前缀和,复杂度约 O ( n 2 3 ) O(n^{\frac{2}{3}}) O(n32)。
一般方法:递归套除法分块,小范围线性筛预处理。
杜教筛上:莫比乌斯函数求和
a n s = ∑ i = 1 n μ ( i ) n ≤ 1 e 11 ans=\sum_{i=1}^{n}\mu(i)\;\;n\leq 1e11 ans=∑i=1nμ(i)n≤1e11
∑ d ∣ n μ ( d ) = [ n = 1 ] \sum_{d|n} \mu(d) = [n = 1] ∑d∣nμ(d)=[n=1]
∑ i = 1 n ∑ d ∣ i μ ( d ) = ∑ d = 1 n ∑ i = 1 n d μ ( i ) = 1 \sum_{i=1}^{n}\sum_{d|i}\mu(d)=\sum_{d=1}^{n}\sum_{i=1}^{\frac{n}{d}}\mu(i) = 1 ∑i=1n∑d∣iμ(d)=∑d=1n∑i=1dnμ(i)=1
1 = ∑ i = 1 n μ ( i ) + ∑ d = 2 n ∑ i = 1 n d μ ( i ) 1 = \sum_{i=1}^{n}\mu(i)+\sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}\mu(i) 1=∑i=1nμ(i)+∑d=2n∑i=1dnμ(i)
a n s = 1 − ∑ d = 2 n ∑ i = 1 n d μ ( i ) ans = 1-\sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}\mu(i) ans=1−∑d=2n∑i=1dnμ(i)
杜教筛艹后面这个式子。
看完杜教筛下后,你就知道其实就是把莫比乌斯函数卷积 1 ( n ) 1(n) 1(n)后转换前缀和就是上面式子的由来。
LL solve_mu(LL n) {
if(n < MXN) return pre_mu[n];
if(mp1[n] == inf) return 0;//unordered_map mp1;
if(mp1[n]) return mp1[n];
LL ans = 1;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans -= (R-L+1LL)%mod*solve_mu(n/L);
}
mp1[n] = ans;
if(mp1[n] == 0) mp1[n] = inf;
return ans;
}
LL solve(LL n) {
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans += solve_mu(R)-solve_mu(L-1);
}
return (ans + mod) % mod;
}
杜教筛上:欧拉函数求和
a n s = ∑ i = 1 n ϕ ( i ) n ≤ 1 e 11 ans=\sum_{i=1}^{n}\phi(i)\;\;n\leq 1e11 ans=∑i=1nϕ(i)n≤1e11
∑ d ∣ n ϕ ( d ) = n \sum_{d|n}\phi(d) = n ∑d∣nϕ(d)=n
∑ i = 1 n ∑ d ∣ i ϕ ( d ) = ∑ d = 1 n ∑ i = 1 n d ϕ ( i ) = n × ( n + 1 ) 2 \sum_{i=1}^{n}\sum_{d|i}\phi(d)=\sum_{d=1}^{n}\sum_{i=1}^{\frac{n}{d}}\phi(i) = \frac{n\times(n+1)}{2} ∑i=1n∑d∣iϕ(d)=∑d=1n∑i=1dnϕ(i)=2n×(n+1)
∑ i = 1 n ϕ ( i ) + ∑ d = 2 n ∑ i = 1 n d ϕ ( i ) = n × ( n + 1 ) 2 \sum_{i=1}^{n}\phi(i)+\sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}\phi(i)=\frac{n\times(n+1)}{2} ∑i=1nϕ(i)+∑d=2n∑i=1dnϕ(i)=2n×(n+1)
a n s = n × ( n + 1 ) 2 − ∑ d = 2 n ∑ i = 1 n d ϕ ( i ) ans = \frac{n\times(n+1)}{2}-\sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}\phi(i) ans=2n×(n+1)−∑d=2n∑i=1dnϕ(i)
杜教筛艹tm的。
同理:这个也是把欧拉函数和 1 ( n ) 1(n) 1(n)卷积。
LL solve_phi(LL n) {
if(n < MXN) return pre_phi[n];
if(mp2[n]) return mp2[n];//unordered_map mp2;
LL ans = n%mod*(n+1)%mod*inv2%mod;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans - (R-L+1LL)%mod*solve_phi(n/L)%mod)%mod;
}
ans = (ans + mod) % mod;
mp2[n] = ans;
return ans;
}
LL solve(LL n) {
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans + solve_phi(R) - solve_phi(L-1) + mod) % mod;
}
return (ans + mod) % mod;
}
杜教筛上:小结
先搞出这个式子 ∑ d ∣ i f ( d ) \sum_{d|i}f(d) ∑d∣if(d),然后利用公式 ∑ i = 1 n ∑ d ∣ i f ( d ) = ∑ d = 1 n ∑ i = 1 n d f ( i ) \sum_{i=1}^{n}\sum_{d|i}f(d)=\sum_{d=1}^{n}\sum_{i=1}^{\frac{n}{d}}f(i) ∑i=1n∑d∣if(d)=∑d=1n∑i=1dnf(i)
∑ i = 1 n f ( i ) + ∑ d = 2 n ∑ i = 1 n d f ( i ) = ∑ i = 1 n ∑ d ∣ i f ( d ) \sum_{i=1}^{n}f(i)+\sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}f(i)=\sum_{i=1}^{n}\sum_{d|i}f(d) ∑i=1nf(i)+∑d=2n∑i=1dnf(i)=∑i=1n∑d∣if(d)
∑ i = 1 n f ( i ) = ∑ i = 1 n ∑ d ∣ i f ( d ) − ∑ d = 2 n ∑ i = 1 n d f ( i ) \sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}\sum_{d|i}f(d) - \sum_{d=2}^{n}\sum_{i=1}^{\frac{n}{d}}f(i) ∑i=1nf(i)=∑i=1n∑d∣if(d)−∑d=2n∑i=1dnf(i)
然后递归+除法分块+线性筛预处理小范围直接算。
杜教筛下:前置:迪利克雷卷积
定义: 定义 f f f, g g g两个积性函数的迪利克雷卷积运算 ( ∗ ) (*) (∗)为:
( f ∗ g ) ( n ) = ∑ d ∣ n f ( d ) × g ( n d ) (f*g)(n)=\sum_{d|n}f(d)\times g(\frac{n}{d}) (f∗g)(n)=d∣n∑f(d)×g(dn)
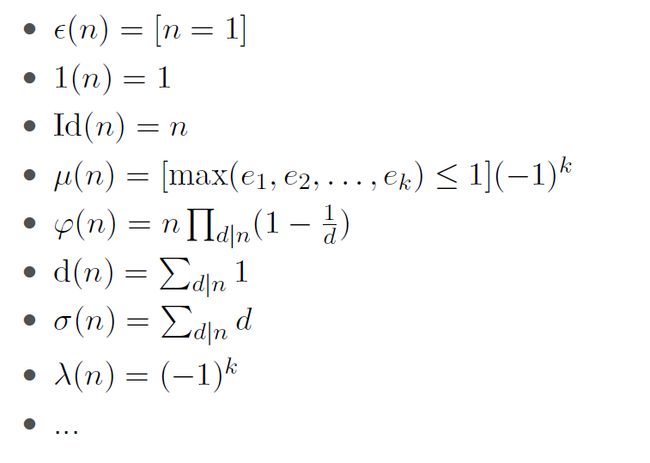
性质:
1.交换律: f ∗ g = g ∗ f f*g=g*f f∗g=g∗f
2.结合律: ( f ∗ g ) ∗ h = f ∗ ( g ∗ h ) (f*g)*h=f*(g*h) (f∗g)∗h=f∗(g∗h)
3.分配律: f ∗ ( g + h ) = f ∗ g + f ∗ h f*(g+h)=f*g+f*h f∗(g+h)=f∗g+f∗h
4.单位元: f ∗ e = f f*e=f f∗e=f
常见函数的卷积:
μ ∗ 1 = ϵ \mu *1=\epsilon μ∗1=ϵ
ϕ ∗ 1 = I d \phi *1=Id ϕ∗1=Id
ϕ = I d ∗ μ \phi = Id * \mu ϕ=Id∗μ
d = 1 ∗ 1 d=1*1 d=1∗1
1 = μ ∗ d 1=\mu * d 1=μ∗d
杜教筛下:求 ∑ i = 1 n ϕ ( i ) × i \sum_{i=1}^{n}\phi(i)\times i ∑i=1nϕ(i)×i
f ( n ) = ϕ ( n ) × n f(n)=\phi(n)\times n f(n)=ϕ(n)×n,直接求不好求,
给它卷积一个 I d Id Id, g ( n ) = n g(n)=n g(n)=n,我们可以得到:
( f ∗ g ) ( n ) = ∑ d ∣ n ϕ ( d ) × d × n d (f*g)(n)=\sum_{d|n}\phi(d)\times d\times \frac{n}{d} (f∗g)(n)=d∣n∑ϕ(d)×d×dn
( f ∗ g ) ( n ) = n ∑ d ∣ i ϕ ( d ) = n 2 (f*g)(n)=n\sum_{d|i}\phi(d)=n^2 (f∗g)(n)=nd∣i∑ϕ(d)=n2
然后我们求这个卷积的前缀和:
∑ i = 1 n ( f ∗ g ) ( i ) = ∑ i = 1 n ∑ d ∣ i g ( d ) × f ( i d ) \sum_{i=1}^{n}(f*g)(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\times f(\frac{i}{d}) ∑i=1n(f∗g)(i)=∑i=1n∑d∣ig(d)×f(di)
= ∑ d = 1 n g ( d ) ∑ d ∣ i f ( i d ) = ∑ d = 1 n g ( d ) ∑ i = 1 n d f ( i ) =\sum_{d=1}^{n}g(d)\sum_{d|i}f(\frac{i}{d})=\sum_{d=1}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i) =∑d=1ng(d)∑d∣if(di)=∑d=1ng(d)∑i=1dnf(i)
= ∑ i = 1 n f ( i ) + ∑ d = 2 n g ( d ) ∑ i = 1 n d f ( i ) = ∑ i = 1 n i 2 =\sum_{i=1}^{n}f(i)+\sum_{d=2}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i)=\sum_{i=1}^{n}i^2 =∑i=1nf(i)+∑d=2ng(d)∑i=1dnf(i)=∑i=1ni2
∑ i = 1 n f ( i ) = ∑ i = 1 n i 2 − ∑ d = 2 n g ( d ) ∑ i = 1 n d f ( i ) \sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}i^2-\sum_{d=2}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i) ∑i=1nf(i)=∑i=1ni2−∑d=2ng(d)∑i=1dnf(i)
到这里就递归+除法分块+线性筛预处理直接算。
杜教筛下:一般方法
比如我们要求 A n s ( n ) = ∑ i = 1 n f ( i ) Ans(n) = \sum_{i=1}^{n}f(i) Ans(n)=∑i=1nf(i)。
直接求会比较难求,这时我们找一个积性函数 g ( n ) g(n) g(n),先求他们卷积的前缀和:
∑ i = 1 n ( f ∗ g ) ( i ) = ∑ i = 1 n ∑ d ∣ i g ( d ) × f ( i d ) \sum_{i=1}^{n}(f*g)(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\times f(\frac{i}{d}) i=1∑n(f∗g)(i)=i=1∑nd∣i∑g(d)×f(di)
= ∑ d = 1 n g ( d ) ∑ d ∣ i f ( i d ) = ∑ d = 1 n g ( d ) ∑ i = 1 n d f ( i ) =\sum_{d=1}^{n}g(d)\sum_{d|i}f(\frac{i}{d})=\sum_{d=1}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i) =d=1∑ng(d)d∣i∑f(di)=d=1∑ng(d)i=1∑dnf(i)
= ∑ i = 1 n f ( i ) + ∑ d = 2 n g ( d ) ∑ i = 1 n d f ( i ) =\sum_{i=1}^{n}f(i)+\sum_{d=2}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i) =i=1∑nf(i)+d=2∑ng(d)i=1∑dnf(i)
g ( 1 ) ∑ i = 1 n f ( i ) = ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ d = 2 n g ( d ) ∑ i = 1 n d f ( i ) g(1)\sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i) g(1)i=1∑nf(i)=i=1∑n(f∗g)(i)−d=2∑ng(d)i=1∑dnf(i)
∑ i = 1 n f ( i ) = ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ d = 2 n g ( d ) ∑ i = 1 n d f ( i ) g ( 1 ) \sum_{i=1}^{n}f(i)=\frac{\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)\sum_{i=1}^{\frac{n}{d}}f(i)}{g(1)} i=1∑nf(i)=g(1)∑i=1n(f∗g)(i)−∑d=2ng(d)∑i=1dnf(i)
A n s ( n ) = ∑ i = 1 n ( f ∗ g ) ( i ) − ∑ d = 2 n g ( d ) A n s ( n d ) g ( 1 ) Ans(n)=\frac{\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)Ans(\frac{n}{d})}{g(1)} Ans(n)=g(1)∑i=1n(f∗g)(i)−∑d=2ng(d)Ans(dn)
- 如果出现 ϕ ( n ) \phi(n) ϕ(n),就凑一下 ∑ d ∣ n ϕ ( d ) = n \sum_{d|n}\phi(d)=n ∑d∣nϕ(d)=n
- 如果出现 μ ( n ) \mu(n) μ(n),就凑一下 ∑ d ∣ n μ ( d ) = [ n = 1 ] \sum_{d|n}\mu(d)=[n=1] ∑d∣nμ(d)=[n=1]
P4213 【模板】杜教筛(Sum)
被卡常数的感觉真不好。
算法解释上面有。。。写道模板题练练手。。。。
#include求 ∑ i = 1 n μ ∗ μ ( i ) \sum_{i=1}^n\mu*\mu(i) ∑i=1nμ∗μ(i)的值
莫比乌斯卷积莫比乌斯的前缀和: ∑ i = 1 n μ ∗ μ ( i ) = ∑ i = 1 n ∑ d ∣ i μ ( d ) × μ ( i d ) \sum_{i=1}^n\mu*\mu(i)=\sum_{i=1}^n\sum_{d|i}\mu(d)\times \mu(\frac id) i=1∑nμ∗μ(i)=i=1∑nd∣i∑μ(d)×μ(di)
化简一下就成这个了: ∑ d = 1 n μ ( d ) ∑ i = 1 n d μ ( i ) \sum_{d=1}^n\mu(d)\sum_{i=1}^{\frac nd}\mu(i) d=1∑nμ(d)i=1∑dnμ(i)
然后套一个求莫比乌斯函数前缀和,预处理一下小范围的卷积+杜教筛就可以了。
还有一种形式,我不太会证明唉: ∑ i = 1 n μ ∗ μ ( i ) = ∑ i = 1 n μ ( i ) − ∑ d = 2 n ∑ i = 1 n d μ ∗ μ ( i ) \sum_{i=1}^n\mu*\mu(i)=\sum_{i=1}^n\mu(i)-\sum_{d=2}^n\sum_{i=1}^{\frac nd}\mu*\mu(i) i=1∑nμ∗μ(i)=i=1∑nμ(i)−d=2∑ni=1∑dnμ∗μ(i)
当然法2比法1要快一点。
CODE:
int noprime[MXN], pp[MXN/2], pcnt;
int mu[MXN], phi[MXN];
int pre_mu[MXN];//mu的前缀和
LL mumu[MXN];//卷积的前缀和
unordered_map<LL,LL>mp1,mp2;
void init_rime() {
noprime[0] = noprime[1] = 1;
mu[1] = 1;mumu[1] = 1;
for(int i = 2; i < MXN; ++i) {
if(!noprime[i]) pp[pcnt++] = i, mu[i]=-1, mumu[i]=-2;
for(int j = 0; j < pcnt && i*pp[j] < MXN; ++j) {
noprime[i*pp[j]] = 1;
mu[i*pp[j]] = -mu[i];
mumu[i*pp[j]] = mumu[i]*mumu[pp[j]];
if(i % pp[j] == 0) {
mu[i*pp[j]] = 0;
if((i/pp[j])%pp[j]) mumu[i*pp[j]] = mumu[i/pp[j]];
else mumu[i*pp[j]] = 0;
break;
}
}
}
for(int i = 1; i < MXN; ++i) pre_mu[i] = pre_mu[i-1] + mu[i];
for(int i = 2; i < MXN; ++i) mumu[i] = (mumu[i]+mumu[i-1]+MOD)%MOD;
}
LL solve_u(LL n) {
if(n < MXN) return pre_mu[n];
if(mp1.count(n)) return mp1[n];
LL ans = 1;
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans - (R-L+1)%MOD*solve_u(n/L)%MOD+MOD)%MOD;
}
mp1[n] = ans;
return ans;
}
LL solve_uu1(LL n) {//方法1
if(n < MXN) return mumu[n];
if(mp2.count(n)) return mp2[n];
LL ans = 0;
for(LL L = 1, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans + (solve_u(R)-solve_u(L-1)+MOD)%MOD*solve_u(n/L)%MOD);
if(ans >= MOD) ans %= MOD;
}
mp2[n] = (ans+MOD)%MOD;
return ans;
}
LL solve_uu2(LL n) {//方法2
if(n < MXN) return mumu[n];
if(mp2.count(n)) return mp2[n];
LL ans = solve_u(n);
for(LL L = 2, R; L <= n; L = R + 1) {
R = n/(n/L);
ans = (ans - (R-L+1)%MOD*solve_uu2(n/L)%MOD+MOD);
if(ans >= MOD) ans %= MOD;
}
mp2[n] = (ans+MOD)%MOD;
return ans;
}
题目
https://blog.csdn.net/Ike940067893/article/details/85036208
https://blog.csdn.net/litble/article/details/80679820
https://blog.csdn.net/fo0Old/article/details/82152479
https://www.cnblogs.com/peng-ym/p/9446555.html
https://blog.csdn.net/VictoryCzt/article/details/80879652
∑ i = 1 n ∑ j = 1 m i × μ ( g c d ( i , j ) ) = ∑ d = 1 n μ ( d ) × d ∑ k = 1 m i n ( n d , m d ) μ ( k ) × k 2 ∑ i = 1 n k d i ∑ j = 1 m k d 1 \sum_{i=1}^{n}\sum_{j=1}^{m}i\times \mu(gcd(i,j))=\sum_{d=1}^{n}\mu(d)\times d\sum_{k=1}^{min(\frac{n}{d},\frac{m}{d})}\mu(k)\times k^2\sum_{i=1}^{\frac{n}{kd}}i\sum_{j=1}^{\frac{m}{kd}}1 i=1∑nj=1∑mi×μ(gcd(i,j))=d=1∑nμ(d)×dk=1∑min(dn,dm)μ(k)×k2i=1∑kdnij=1∑kdm1