【MATLAB信号处理】连续时间信号与系统的复频域分析
连续时间信号与系统的复频域分析
- 拉普拉斯变换的MATLAB实现
- 零极点分布图
- 复频域法1
- 复频域法2
拉普拉斯变换的MATLAB实现
(1) 已知信号 f ( t ) = cos ( 2 t ) sin ( 3 t ) u ( t ) f(t)=\cos(2t)\sin(3t)u(t) f(t)=cos(2t)sin(3t)u(t),试调用laplace函数计算其拉普拉斯变换。
(2) 已知某连续系统的系统函数如下,试计算拉普拉斯逆变换。
H 1 ( s ) = ( s + 1 ) ( s + 4 ) s ( s + 2 ) ( s + 3 ) H_1(s)=\frac{(s+1)(s+4)}{s(s+2)(s+3)} H1(s)=s(s+2)(s+3)(s+1)(s+4), H 2 ( s ) = s 3 + 5 s 2 + 9 s + 7 s 2 + 3 s + 2 H_2(s)=\frac{s^3+5s2+9s+7}{s^2+3s+2} H2(s)=s2+3s+2s3+5s2+9s+7
syms t;
f = cos(2*t)*sin(3*t)*heaviside(t);
L = laplace(f);
display(L);
syms s;
H1 = ((s+1)*(s+4))/(s*(s+2)*(s+3));
h1 = ilaplace(H1);
display(h1);
H2 = (s^3+5*s^2+9*s+7)/(s^2+3*s+2);
h2 = ilaplace(H2);
display(h2);
零极点分布图
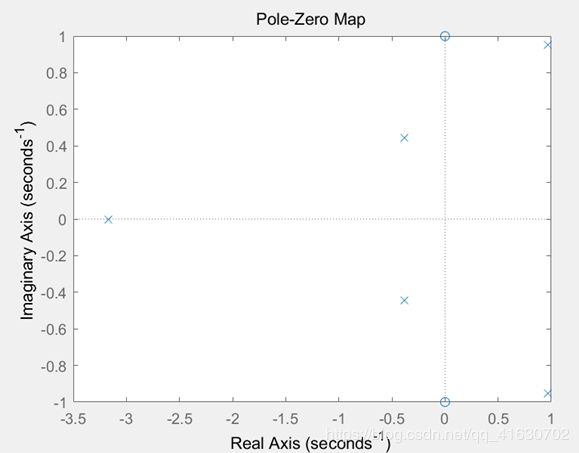
已知某连续系统的系统函数如下,试利用MATLAB绘出其零、极点分布图,并判断系统是否稳定。
H ( s ) = s 2 + 1 s 5 + 2 s 4 − 3 s 3 + 3 s 2 + 3 s + 2 H(s)=\frac{s^2+1}{s^5+2s^4-3s^3+3s^2+3s+2} H(s)=s5+2s4−3s3+3s2+3s+2s2+1
a = [1, 0, 1];
b = [1,2,-3,3,3,2];
sys = tf(a, b);
pzmap(sys);
pole = pole(sys);
zero = zero(sys);
复频域法1
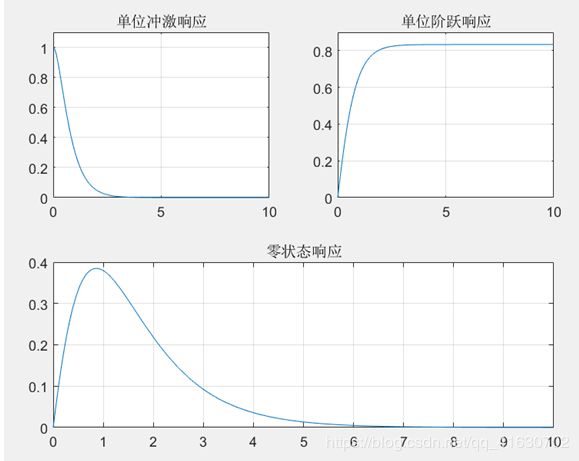
已知系统传递函数为: H ( s ) = s + 5 s 2 + 5 s + 6 H(s)=\frac{s+5}{s2+5s+6} H(s)=s2+5s+6s+5,利用MATLAB复频域方法求解:
(1) 系统的单位冲激响应。
(2) 系统的单位阶跃响应。
(3) 输入 f ( t ) = e − t u ( t ) f(t)=e^{-t}u(t) f(t)=e−tu(t)时的系统零状态响应。
a = [1, 5];
b = [1, 5, 6];
t = 0:0.01:10;
h = impulse(a, b, t);
subplot(2, 2, 1);
plot(t, h);
axis([0, 10, 0, 1.1]);
title('单位冲激响应');grid on;
syms s t;
H = (s+5)/(s^2+5*s+6);
F = laplace(heaviside(t));
Y = H*F;
y = ilaplace(Y);
subplot(2, 2, 2);
fplot(y*heaviside(t));
axis([0, 10, 0, 0.9]);
title('单位阶跃响应');
grid on;
f = exp(-t)*heaviside(t);
Fs = laplace(f);
Ys = H*Fs;
yts = ilaplace(Ys);
subplot(2, 2, [3, 4]);
fplot(yts*heaviside(t));
axis([0, 10, 0, 0.4]);
title('零状态响应');
grid on;
复频域法2
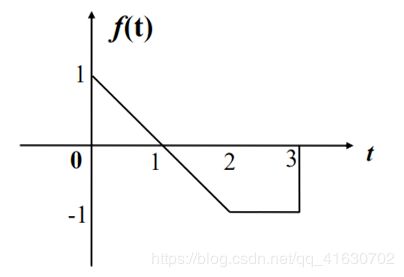
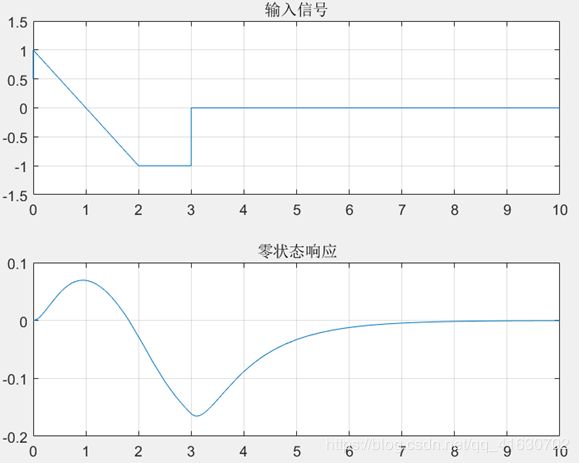
已知某连续系统的系统函数如下,其中输入信号的波形如图,利用MATLAB求解并绘出系统零状态响应。
H ( s ) = 1 s 2 + 5 s + 4 H(s)=\frac{1}{s^2+5s+4} H(s)=s2+5s+41
syms t s;
f = (-t+1)*(heaviside(t)-heaviside(t-2))-(heaviside(t-2)-heaviside(t-3));
subplot(2, 1, 1);
fplot(f);
axis([0, 10, -1.5, 1.5]);
title('输入信号');
grid on;
subplot(2, 1, 2);
F = laplace(f);
H = 1/(s^2+5*s+4);
Y = F*H;
y = ilaplace(Y);
fplot(y);
axis([0, 10, -0.2, 0.1]);
title('零状态响应');
grid on;