学习笔记(一)|| 感知器与感知器神经网络
感知器与感知器神经网络
- 1. 感知器
- 1. 1单层感知器原理
- 1.2 感知器算法
- 2. 代码实现及解读
- 2.1 感知器神经网络的构建
- 2.1.1生成网络
- 代码实现
- 代码说明
- 2.1.2 网络仿真
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.1.3 网络初始化
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.2 感知器神经网络的学习和训练
- 2.2.1 网络学习
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.2.1 网络训练
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.3 二输入感知器分类可视化问题
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.4 标准化学习规则训练奇异样本
- 代码实现
- 运行结果
- 代码及运行结果说明
- 2.5 设计多个感知器神经元解决分类问题
- 代码实现
- 运行结果
- 代码及运行结果说明
1. 感知器
1. 1单层感知器原理
单层感知器由一个线性组合器和一个二值阈值元件组成。
输入是一个N维向量 x=[x1,x2,…,xn],其中每一个分量对应一个权值wi,隐含层输出叠加为一个标量值:
v = ∑ i = 1 N x i w i v=\sum_{i=1}^N{x_{i}w_{i}} v=i=1∑Nxiwi
随后在二值阈值元件中对得到的v值进行判断,产生二值输出:
s g n ( x ) = { 1 v ≥ 0 0 v < 0 sgn(x)= \begin{cases} 1& { v≥0}\\ 0& { v<0} \end{cases} sgn(x)={10v≥0v<0
单层感知器结构图:
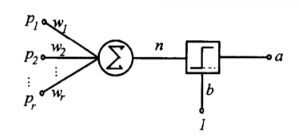
单层感知器进行模式识别的超平面由下式决定:
∑ i = 1 N x i w i + b = 0 \sum_{i=1}^N{x_{i}w_{i}}+b=0 i=1∑Nxiwi+b=0
当维数N=2时,输入向量可以表示为平面直角坐标系中的一个点。此时分类超平面是一条直线:
w 1 x 1 + w 2 x 2 + b = 0 w_1x_1+w_2x_2+b=0 w1x1+w2x2+b=0
这样就可以将点沿直线划分成两类。
1.2 感知器算法
输入:训练数据T={(x1,y1),(x2,y2),···,(xN,yN)},学习率η
输出:w,b,即感知器模型
1.w,b权值初始化;
2.选取训练数据(xi,yi);
3.如果 yi(wxi+b)≤0 则:
w ← w+ηyixi
b ← b+ηyi
4.转至step2,直至训练数据集中没有误分类点或满足终止条件。
PS:学习过程可选批量梯度下降
2. 代码实现及解读
2.1 感知器神经网络的构建
2.1.1生成网络
代码实现
net=newp([0 2],1);%单输入,输入值为[0,2]之间的数
inputweights=net.inputweights{1,1};%第一层的权重为1
biases=net.biases{1};%阈值为1
代码说明
newp函数:
net=newp(P,T,TF,LF)
newp()函数可用于创建一个感知器
P:是一个R*2矩阵,矩阵行数R等于输入向量的维数。R行就输入R个分量向量,2代表分量向量的输入范围。
如 P = [-1,1;0,1] 就是每个输入向量输入两个分量向量,范围为 -1~1 和 0 ~1。
T:表示输出节点的个数,标量。
TF:传输函数。可取值为hardlim或hardlims,默认为hardlim。
hardlims:
s g n ( x ) = { 1 x≥0 − 1 x<0 sgn(x)= \begin{cases} 1& \text{x≥0}\\ -1& \text{x<0} \end{cases} sgn(x)={1−1x≥0x<0
hardlim:遇到负数,输出值为0而不是-1。
LF:学习函数,可取值为learnp或learnpn,默认值learnp 输入向量数值幅度变化较大时,采用learnpn代替learnp,可以加快计算速度。
net:返回的感知器网络。
2.1.2 网络仿真
代码实现
net=newp([-2 2;-2 2],1);%两个输入,一个神经元,默认二值激活
net.IW{1,1}=[-1 1];%权重,net.IW{i,j}表示第i层网络第j个神经元的权重向量
net.IW{1,1}
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)
运行结果
>> Perceptron
ans =
-1 1
ans =
1
p1 =
1
1
a1 =
1
p2 =
1
-1
a2 =
0
p3 =
[2x1 double] [2x1 double]
a3 =
[1] [0]
p4 =
1 1
1 -1
a4 =
1 0
a1 =
1
>>
代码及运行结果说明
根据输出net.IW{1,1}和net.b{1}的值可以得到当前单层感知器的两个输入的加权分别为-1、1,其阈值为1。
点p1(1,1),p2(1,-1)分别使用sim()函数进行网络仿真,p1(1,1)的各个输入乘以相应权重相加可得总和为0,在二值阈值元件中对得到的0进行判断,其大于等于0,产生二值输出1。p2(1,-1)同理。p3将两组数据放在一起使用sim()函数进行网络仿真,输出a3 = [1] [0]。p4将两组数据放在矩阵里得到输出a4 = [1] [0]。
重新设置感知器的权重向量为3,4,阈值为1,对p1重新进行网络仿真得到的总和为1,在二值阈值元件中对得到的1进行判断,其大于等于0,产生二值输出1。
2.1.3 网络初始化
代码实现
% 1.3 网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
% 改变权值和阈值为随机数
net.inputweights{1,1}.initFcn='rands';
net.biases{1}.initFcn='rands';
net=init(net);
bias=net.b{1}
wts=net.IW{1,1}
a1=sim(net,p1)
运行结果
wts =
0 0
bias =
0
bias =
0.6294
wts =
0.8116 -0.7460
a1 =
1
>>
代码及运行结果说明
init()函数重新将整个网络的权值和阈值初始化,将权值和阈值重新归零。
将网络的初始化权重和初始化阈值的参数通常设为rands,使其在-1到1之间随机取值。
可以初始化后的阈值为0.6294,两个输入层的权重分别为 0.8116 、-0.7460,将p1(1,1)输入进行网络仿真可得1* 0.8116 +1* (-0.7460)=0.0656>0, 通过二值激活函数可的输出为1。
2.2 感知器神经网络的学习和训练
2.2.1 网络学习
代码实现
% 2. 感知器神经网络的学习和训练
% 1 网络学习
net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
help learnp
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)
net = newp([0 1; -2 2],1);
P = [0 0 1 1; 0 1 0 1];
T = [0 1 1 1];
Y = sim(net,P)
net.trainParam.epochs = 20;
net = train(net,P,T);
Y = sim(net,P)
运行结果
>> Perceptron
w =
1.0000 -0.8000
a =
0
e =
1
dw =
1 2
w =
2.0000 1.2000
a =
1
Y =
1 1 1 1
Y =
0 1 1 1
>>
nntraintool窗口:
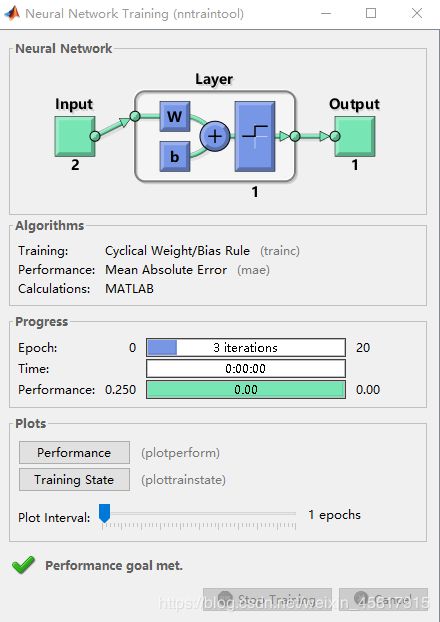
Performance绘图结果:
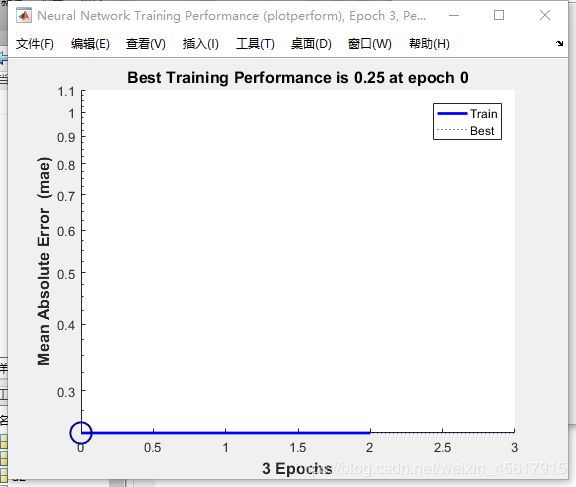
代码及运行结果说明
learnp()函数:单步训练
用于感知器神经网络权值和阈值的学习,学习规则是调整网络的权值和阈值,使网络平均绝对误差性能最小。
train()函数:连续训练
将全体样本输入到网络中学习。
通过网络net中的属性参数(epochs)来设置训练迭代的最大值。。
注意:
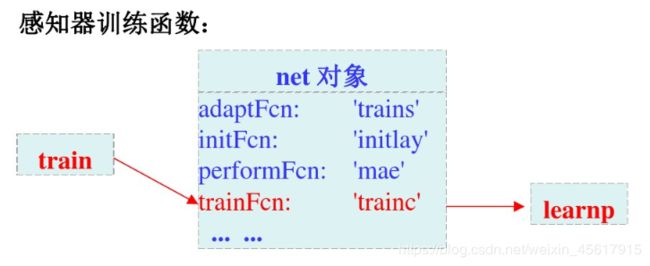
可知train()函数最终调用的仍是learnp()函数。
代码段首先构造了一个二输入感知器网络,其输入权值分别为1,0.8,阈值为0。将p(1,2)输入此感知器网络进行网络仿真得到输出0,代码断种设置了期望得到的输出t为1,可计算得到误差e=t-a=1,将感知器网络的各个输入权值、p(1,2)、e通过learn()函数得到各个权值需要修正的值分为别1,2,修正后的感知器权值为2、1.2,再次将pp(1,2)输入修正后的感知器网络进行网络仿真得到期望的输出值1。
其次代码段构造了一个初始值均为0的感知器网络,规定其为二值输入且其输入范围分别为0~ 1、-2~2。输入4个样本向量及其期望输出的值使用train()函数训练感知器网络的权值和阈值。训练结束再次对4个样本进行网络仿真得到的输出值与期望输出值相等,即训练出的感知器网络可以得到期望输出。
2.2.1 网络训练
代码实现
% 2 网络训练
net=init(net);
p1=[2;2];t1=0;p2=[1;-2];t2=1;p3=[-2;2];t3=0;p4=[-1;1];t4=1;
net.trainParam.epochs=1;
net=train(net,p1,t1)
w=net.IW{1,1}
b=net.b{1}
a=sim(net,p1)
net=init(net);
p=[[2;2] [1;-2] [-2;2] [-1;1]];
t=[0 1 0 1];
net.trainParam.epochs=1;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=2;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=20;
net=train(net,p,t);
a=sim(net,p)
运行结果
>> Perceptron
net =
Neural Network
name: 'Custom Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 1
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 3
sampleTime: 1
connections:
biasConnect: true
inputConnect: true
layerConnect: false
outputConnect: true
subobjects:
input: Equivalent to inputs{1}
output: Equivalent to outputs{1}
inputs: {1x1 cell array of 1 input}
layers: {1x1 cell array of 1 layer}
outputs: {1x1 cell array of 1 output}
biases: {1x1 cell array of 1 bias}
inputWeights: {1x1 cell array of 1 weight}
layerWeights: {1x1 cell array of 0 weights}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: (none)
divideParam: (none)
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mae'
performParam: .regularization, .normalization
plotFcns: {'plotperform', plottrainstate}
plotParams: {1x2 cell array of 2 params}
trainFcn: 'trainc'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .max_fail
weight and bias values:
IW: {1x1 cell} containing 1 input weight matrix
LW: {1x1 cell} containing 0 layer weight matrices
b: {1x1 cell} containing 1 bias vector
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
w =
-2 -2
b =
-1
a =
0
a =
0 0 1 1
a =
0 1 0 1
a =
0 1 0 1
>>
nntraintool窗口:

Performance绘图结果:

代码及运行结果说明
代码段对p1(2,2)及其期望输出值进行网络训练得到训练后的感知器网络,其二输入的权值分别为-2、-2,阈值为-1。
其次对于4个样本点及四个期望值进行网络训练,分别设置net.trainParam.epochs的值为1,2,20,由输出结果与期望输出值对比当训练迭代的最大值为1的时候训练出的感知器网络无法得到4个样本的期待输出,只有当训练迭代的最大值较大时才可以训练出适合4个样本的感知器网络。
2.3 二输入感知器分类可视化问题
代码实现
% 3. 二输入感知器分类可视化问题
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=newp([-1 1;-1 1],1);
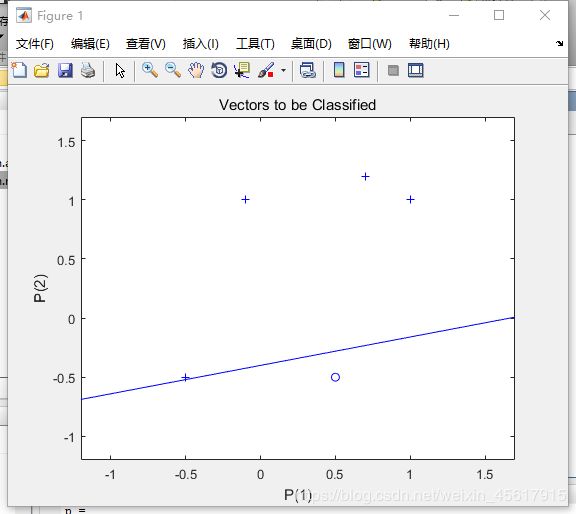
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1});
%hold on;
%plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
plotpc(net.IW{1},net.b{1})
%仿真
a=sim(net,p);
plotpv(p,a)
p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
%感知器能够正确分类,从而网络可行。
运行结果
>> Perceptron
T =
1 1 0 1
ans =
-0.5000 0.5000
ans =
-1
ans =
-0.1000 2.0000
ans =
2
net =
Neural Network
name: 'Custom Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 1
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 3
sampleTime: 1
connections:
biasConnect: true
inputConnect: true
layerConnect: false
outputConnect: true
subobjects:
input: Equivalent to inputs{1}
output: Equivalent to outputs{1}
inputs: {1x1 cell array of 1 input}
layers: {1x1 cell array of 1 layer}
outputs: {1x1 cell array of 1 output}
biases: {1x1 cell array of 1 bias}
inputWeights: {1x1 cell array of 1 weight}
layerWeights: {1x1 cell array of 0 weights}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: (none)
divideParam: (none)
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mae'
performParam: .regularization, .normalization
plotFcns: {'plotperform', plottrainstate}
plotParams: {1x2 cell array of 2 params}
trainFcn: 'trainc'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .max_fail
weight and bias values:
IW: {1x1 cell} containing 1 input weight matrix
LW: {1x1 cell} containing 0 layer weight matrices
b: {1x1 cell} containing 1 bias vector
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
ans =
-0.6000 2.5000
ans =
1
p =
0.7000
1.2000
>>
代码及运行结果说明
plotv()函数:用于在坐标中绘制给定的样本点及其类别。
plotpc()函数:用于绘制感知器分界线。
adapt()函数:该函数为学习自适应函数,其在每一个输入时间阶段更新网络时仿真网络。adapt()函数返回一个新的能更好的执行分类、网络的输出、和误差的神经网络,这个划线函数允许网络从3个角度去调整,划分类线一直到误差为0.
代码段使用adapt()函数进行感知器网络学习自适应调整权值和阈值,通过调整net.adaptParam.passes的值设置训练过程中的迭代次数。
未设置net.adaptParam.passes值的划线情况:
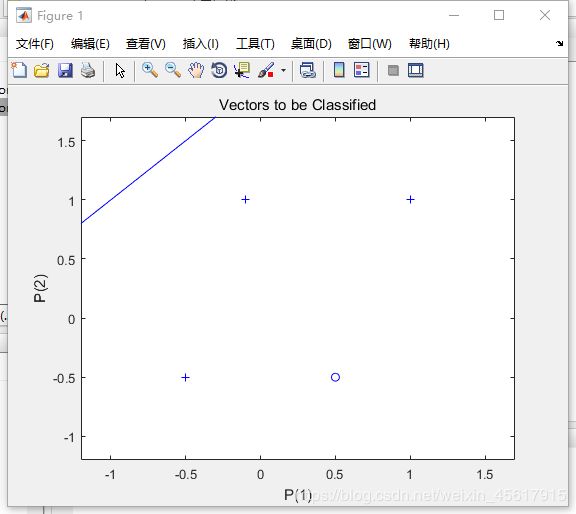
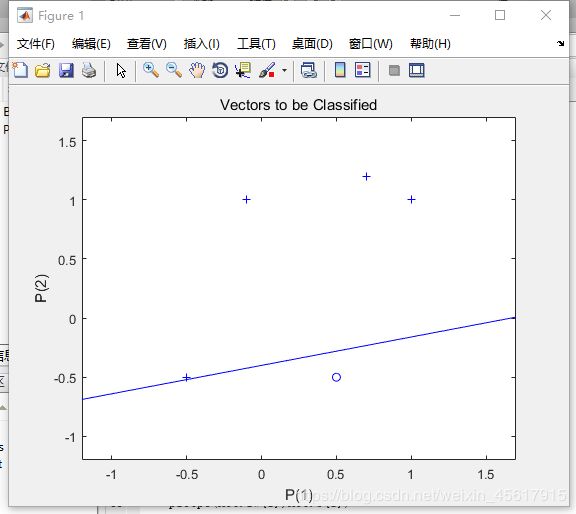
net.adaptParam.passes值为3的划线情况:
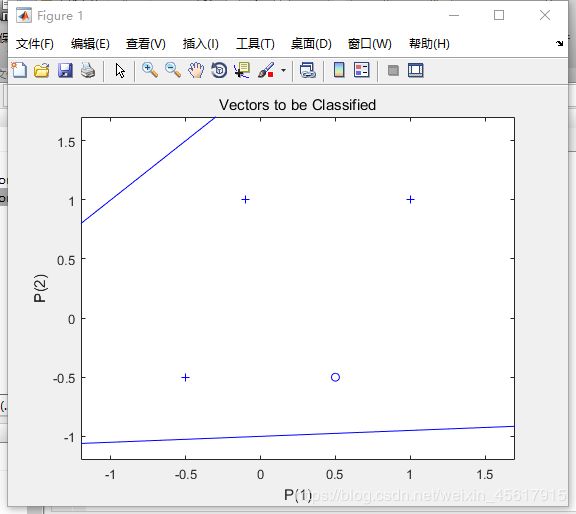
net.adaptParam.passes值为6的划线情况:

由此可知:net.adaptParam.passes的值越大,分类划线更准确。即训练过程中的迭代次数越多得到的网络更加准确。
当网络中重新输入了p(0.7,1.2)时,通过自适应函数网络会根据新输入的向量更新网络,重新构建一个适用于所有样本的感知器网络。
2.4 标准化学习规则训练奇异样本
代码实现
% 4. 标准化学习规则训练奇异样本
P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);%标出所有点
hold on;
linehandle=plotpc(net.IW{1},net.b{1});%画出分类线
E=1;
net.adaptParam.passes=3;%passes决定在训练过程中训练值重复的次数。
while (sse(E))
[net,Y,E]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%另外一种网络修正学习(非标准化学习规则learnp)
hold off;
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%无法正确分类
%标准化学习规则网络训练速度要快!
% 训练奇异样本
% 用标准化感知器学习规则(标准化学习数learnpn)进行分类
net=newp([-40 1;-1 50],1,'hardlim','learnpn');
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}%权重
net.b{1}%阈值
%正确分类
%非标准化感知器学习规则训练奇异样本的结果
net=newp([-40 1;-1 50],1);
net.trainParam.epochs=30;
net=train(net,P,T);
pause;
linehandle=plotpc(net.IW{1},net.b{1});
hold on;
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
运行结果
>> Perceptron
P =
-0.5000 -0.5000 0.3000 -0.1000 -40.0000
-0.5000 0.5000 -0.5000 1.0000 50.0000
ans =
-45.0000 10.5000
ans =
-17
ans =
-0.2000 -0.5000
ans =
-2
ans =
-1.5592 -0.1980
ans =
0
>>
样本分类绘图结果:
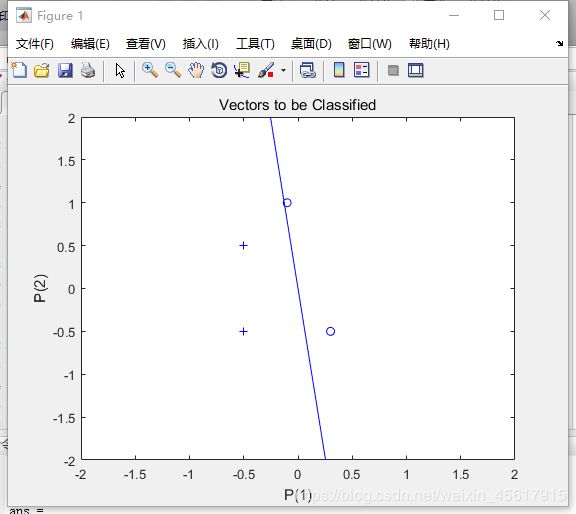
nntraintool窗口:
Performance绘图结果:
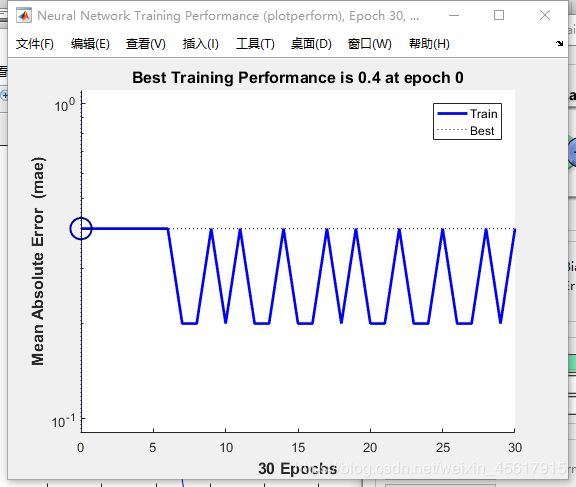
代码及运行结果说明
nntraintool窗口参数详解:
Neural Network:
这里显示的是输入大小,中间层数量以及每层的神经元个数。
Algorithms:
Training:Cyclical Weight/Bias Rule。这表示学习训练函数。
Performance:Mean Squared Error。这表示性能用均方误差来表示。
Calculations: MATLAB。
Progress
Epoch:迭代次数。
Time:运行时间。
Performance:训练数据集的性能。
Plots:
Performance:这里可以点进去,看train的性能。
Training State:记录Gradient和Validation Checks。
奇异样本:奇异样本是数值上远远偏离其他样本的数据。
当网络的输入样本中存在奇异样本时,训练时间将大大增加。
2.5 设计多个感知器神经元解决分类问题
代码实现
% 5. 设计多个感知器神经元解决分类问题
p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
运行结果
>> Perceptron
p =
1.0000 1.2000 2.0000 -0.8000
2.0000 0.9000 -0.5000 0.7000
t =
1 1 0 1
0 1 1 0
>>
代码及运行结果说明
see(e)函数:是用来判定误差e的函数。
此代码段构建具有两个感知器神经元的神经网络解决分类问题,代码段中使用while循环进行自适应网络学习,当see(e)函数判定当前误差为0时,跳出循环,迭代结束。
每一次循环中都使用自适应函数进行网络学习,再进行绘制感知器分界线。当跳出循环时,显示最后一次自适应网络学习和绘制分界线的结果。
可以看到当使用两个感知器神经元训练出来的网络可以解决较为复杂的分类问题。