Educational Codeforces Round 85 (Rated for Div. 2)题解报告

A.Level Statistics

题目大意：

  有n(<=100)个时刻，按照时间顺序1-n，告诉你前i时刻的玩的总次数，以及通过关卡的总次数
  问：判断给出的n个时刻玩的总次数以及通过关卡的总次数，是否都正确，都正确则输出"YES",否则输出"NO"

解题思路：

  （1）前i时刻玩的总次数肯定多于通过关卡的总次数
  （2）玩的总次数以及通过关卡的总次数是递增的
  （3）第i-1时刻到第i时刻增加的玩的总次数肯定多于通过关卡的次数

AC代码：

#include
using namespace std;
int T,n,vis;
int p[200],c[200];
int main() {
	scanf("%d",&T);
	while(T--) {
		vis=1;//vis为1说明全部数据都正确
		scanf("%d",&n);
		for(int i=1; i<=n; i++) scanf("%d%d",&p[i],&c[i]);
		for(int i=1; i<=n; i++) {
			if(p[i]>=c[i]&&p[i]-p[i-1]>=c[i]-c[i-1]&&p[i]>=p[i-1]&&c[i]>=c[i-1]) continue;
			//判断条件成立，则continue
			else vis=0;
		}
		if(vis) printf("YES\n");
		else printf("NO\n");
	}
} 

B.Middle Class

题目大意：

  有个长度为n（1<=n<=1e5）的a数组（1<=ai<=1e9）,你可以选择其中一些位置，平分它们的值到这些位置
  给定一个x（1<=x<=1e9），问经过若干次这样的操作，a数组中大于等于x的个数最多是多少？

解题思路：

  这道题就是一道简单的贪心，先从大到小排序
  从大到小先选取大于等于x的并累加其个数ans和值sum;
  对于小于x的a[i]，先判断(sum+a[i])/(ans+1)是否大于等于x，如果大于等于则可选取该a[i]并进行累加,不满足的话则可以直接跳出for循环，因为之后的都比a[i]小了

AC代码：

#include
using namespace std;
int T,n,x,ans;
double sum;
double a[200000];
bool cmp(const int & b,const int & c) {
	return b>c;
}
int main() {
	scanf("%d",&T);
	while(T--) {
		sum=0,ans=0;
		scanf("%d%d",&n,&x);
		for(int i=1; i<=n; i++) scanf("%lf",&a[i]);
		sort(a+1,a+n+1,cmp);//从大到小排序
		for(int i=1; i<=n; i++)
			if(a[i]>=x||(sum+a[i])/(ans+1)>=x) sum+=a[i],ans++;
			//两种情况的判断
			else continue;//其实这里break也可以
		printf("%d\n",ans);
	}
}

C.题目大意

  有n个怪兽，第i位置的怪兽血量值a[i]，如果i位置的怪兽死亡会对i+1位置怪兽造成b[i]的伤害（如果是第n个怪兽死亡，对第一个怪兽造成伤害），你可以射击某个怪兽每次射击扣怪兽的一滴血量。
  问最少射击多少次能使全部怪兽死亡。

解题思路：

  关于这道题首先明确的几点：
  （1）要么就不打，要么就打完这个怪兽（为了算法的简便）
  （2）选择一个开始之后就一直往下打就行，而不是选定一个，打完一段之后，再重新选择一个开始往下打（为了使答案是最优的）
  

证明：

  （1）
    对于1…i…j…n的怪兽，假设先打j的一些血，在把i打爆，使接连的爆炸能够炸到j。那么无疑把j怪兽打掉a[j]-b[j-1]，能够使打爆i怪兽之后（假设能爆炸到j-1，刚好使j怪兽恰好爆掉。
    为了算法的简便，我们可以先打爆i怪兽再接着打j怪兽的a[j]-b[j-1]滴血
  （2）
    假设一开始选定i怪兽，把其打爆之后，所受到波及怪兽死亡的范围为[i,k],如果不接着k+1继续打，假设从j（j=k+2）位置开始打，那么最后还是要单独打一次k+1,而且第k+1的怪兽的爆炸对k+2的怪兽不会有作用（因为打掉了，而且是用了a[k+2]的代价，如果打了a[k+1],则打第k+2的怪兽，则只需要max{a[k+2]-b[k+1],0}     那么第k+1位置的怪兽都要打，所以只用比较第k+2的怪兽位置所耗费的子弹就行，到此（2）证明完毕
  由(1)(2)题目也转变成，选一个怪兽一直打下去，打完怪兽的最少子弹是多少?

解题：

  现在的目的就是怎样在O(1)的时间计算出选第i个开头，所需要的子弹数？
  利用一个c数组，c[i]=max{a[i]-b[i-1],0}（如果i==1，那么c[1]=max{a[1]-b[n],0）,用来记录当i-1的怪兽爆炸之后，再打i怪兽所需要的子弹数。
  那这有什么用呢？
  选定一个特殊位置，如果从第一个位置开始打，那么所需的子弹总数=a[1]+c[2]+c[3]+…+c[n]。
  c[2]+…+c[n]不就是从2位置开始c数组的后缀和吗！！！
  设sum[i]为i~n的c数组的后缀和
  任选一个点i,那么就能推出它所需的子弹总数=a[i]+sum[i+1]+sum[1]-sum[i]（sum[1]-sum[i]是[1,i-1]区间所需的子弹数）

AC代码：

#include
using namespace std;
typedef long long ll;
ll T,n,ans;
ll a[300100],b[300100],c[300100],sum[300100];
int main() {
	scanf("%lld",&T);
	while(T--) {
		scanf("%lld",&n);
		sum[n+1]=0;
		for(int i=1; i<=n; i++) scanf("%lld%lld",&a[i],&b[i]);
		c[1]=max(a[1]-b[n],(ll)0);//1位置比较特殊，先算
		for(int i=2; i<=n; i++) c[i]=max(a[i]-b[i-1],(ll)0);
		for(int i=n; i>=1; i--) sum[i]=sum[i+1]+c[i];
		//计算c数组的后缀和
		ans=a[1]+sum[2];//1位置比较特殊，先算
		for(int i=2; i<=n; i++) ans=min(ans,a[i]+sum[i+1]+sum[1]-sum[i]);
		//每次比较最小值就可以了，注意第n个位置，因为sum[n+1]==0
		//所以不需要额外拿出来比较
		printf("%lld\n",ans);
	}
}

D.Minimum Euler Cycle

题目大意：

  给你一副结点数为n的有向完全图，找到这样一条能够遍历所有边（每条边只遍历一次，点可以遍历多次），字典序且最小的路径，在给定的L,R范围内，输出即可。(2≤n≤1e5, 1≤L≤R≤n(n−1)+1, R−L+1≤1e5)

解题思路：

  （暂时不会用电脑画图，就看我手画的把…）
  
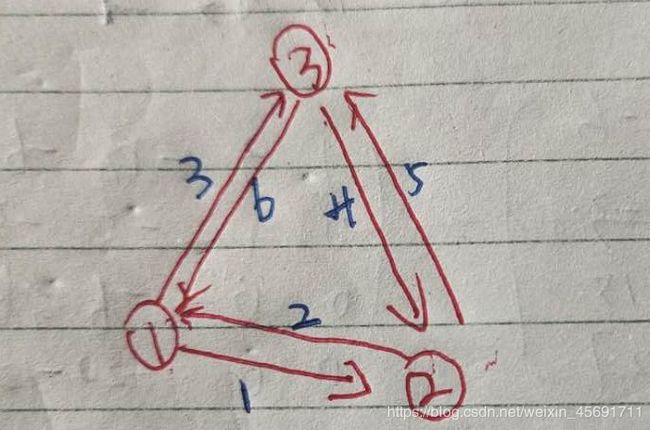
  对于3个结点的有向完全图最优路径：1->2->1->3->2->3->1
  对于4个结点的有向完全图最优路径：1->2->1->3->1->4->2->3->2->4->3->4->1
…
  对于n个结点的我们可以大胆猜测为：1 2 1 3 … 1 n 2 3… 2 n…n-1 n 1
  由这个规律写代码即可。(可以试着反证，因为这样是可以遍历所有点的，如果替换掉其中任意几点，那么不可能更优)
  因为要找的L到R的区间内的路径，而且n^2约为1e10全部存起来显然不现实，所以我们要进一步找其中的规律
  对于n=4的情况，最优路径为：1 2 1 3 1 4 2 3 2 4 3 4 1
  可以发现，当每隔一个数就为1的情况有6个，每隔一个数为2的情况有4，3的情况有2个，最后再有一个回到开始点的1个
  由等差数列求和公式，当每隔一个数为k时的总数位k*(2n-1-k)
  下面的AC代码，笔者能力有限，写的有点乱，如若看不懂，可以自己手模一下，或者留言评论，请见谅

AC代码：

#include
using namespace std;
typedef long long ll;
ll T,n,l,r,x,k,Start,End;
ll a[1000100];
int main() {
	scanf("%lld",&T);
	while(T--) {
		scanf("%lld%lld%lld",&n,&l,&r);
		for(k=0; k<=n-1; k++) 
		    if(k*(2*n-1-k)<=l&&(k+1)*(2*n-1-(k+1))>=l)//找到从哪个k开始记录
		        break;
		ll tmp=k,x=k+2,loc=0,tot=1;
		for(ll i=k*(2*n-1-k); i<=r; i++) {
			if(i==0) {
				tmp++;
				tot=1;
				x=tmp+1;
				continue;
			}
			if(i==l) Start=loc+1;//找起点
			if(i==r) End=loc+1;//找终点
			if(i==tmp*(2*n-1-tmp)) {
				a[++loc]=n;//说明到了每隔一个数为tmp的最后一位n
				tmp++;//加一
				tot=1;
				x=tmp+1;//要从tmp+1开始
			}
			else {
				if(tot&1) a[++loc]=tmp;//如果tot为奇数则为tmp
				else a[++loc]=x,x++;//否则为x，然后x++
				tot++; 
			}
		}
		if(r==n*(n-1)+1) a[End]=1;//注意如果为n*(n-1)+1那么最后一个数为1
		for(ll i=Start; i<=End; i++) printf("%lld ",a[i]);
		printf("\n");
	}
}

如有错误，或者改进建议，欢迎留言！！！