点云处理——孔洞修补

之前在做基于点云的孔洞修补研究，参考了一些学位论文后选择了一种基于自己能力能够复现的简单算法，虽然最终效果一般，不过在这个过程中收获了很多，特此记录。
基于点云的孔洞修补与基于三角网格的孔洞修补相比，点云本身的复杂性和边界不确定性就决定了其在孔洞识别和修补上的困难度。
修补前的滤波工作很重要，滤的不够噪声点会对修补造成很大影响，但滤的太多又很容易丢失孔洞原有的形状，难以识别。所以最后选择仅对点云中的闭合孔洞进行识别修补，并采用一种基于邻域信息不断扩张边界的方法，见参考文献。

1.平均点距计算

平均点距用来为后续半径搜索和孔洞填充阈值的设定提供参考，可以使用空间分块策略进行估算。
（1）计算出包含全部点云的最小包围盒，得到x,y,z三个轴向上的长度dx,dy,dz。
（2）计算预估栅格边长L，使用公式：

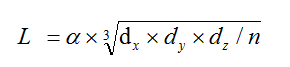
（3）使用长宽高均为L的立方体将最小包围盒栅格化，可得到全部栅格数N。
（4）遍历所有点云数据，将其置入栅格中，可以统计得到非空栅格数Ncell，使用公式即可估算出整幅点云的平均点距：

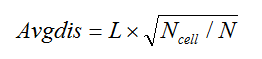
float AvgDis(pcl::PointCloud<pcl::PointXYZRGB>::Ptr cloud_ptr)
{
	pcl::PointCloud<pcl::PointXYZRGB>::iterator it;
	float max_x, max_y, max_z, min_x, min_y, min_z;
	float _distanceX, _distanceY, _distanceZ;
	float _length;
	float _Avgdis;
	int Ncell, Nall, num;
	Ncell = 0;
	num = cloud_ptr->points.size();
	max_x = min_x = cloud_ptr->points[0].x;
	max_y = min_y = cloud_ptr->points[0].y;
	max_z = min_z = cloud_ptr->points[0].z;
	for (size_t i = 0; i < num; i++){
		if (cloud_ptr->points[i].x>max_x){
			max_x = cloud_ptr->points[i].x;
		}
		if (cloud_ptr->points[i].x<min_x){
			min_x = cloud_ptr->points[i].x;
		}
		if (cloud_ptr->points[i].y>max_y){
			max_y = cloud_ptr->points[i].y;
		}
		if (cloud_ptr->points[i].y<min_y){
			min_y = cloud_ptr->points[i].y;
		}
		if (cloud_ptr->points[i].z>max_z){
			max_z = cloud_ptr->points[i].z;
		}
		if (cloud_ptr->points[i].z<min_z){
			min_z = cloud_ptr->points[i].z;
		}
	}
	_distanceX = max_x - min_x;
	_distanceY = max_y - min_y;
	_distanceZ = max_z - min_z;
	_length = pow((_distanceX*_distanceY*_distanceZ / num), 1.0 / 3);   //此处没有设置标量alpha，当其为1
	std::cout << "length is " << _length << std::endl;
	int xNum, yNum, zNum;
	xNum = _distanceX / _length + 1;
	yNum = _distanceY / _length + 1;
	zNum = _distanceZ / _length + 1;
	Nall = xNum*yNum*zNum;
	std::cout << "Nall is " << Nall << std::endl;
	int ***Box;
	Box = new int **[xNum];
	for (int i = 0; i < xNum; ++i)
		Box[i] = new int*[yNum];
	for (int i = 0; i < xNum; ++i){
		for (int j = 0; j < yNum; ++j)
			Box[i][j] = new int[zNum];
	}
	for (int i = 0; i < xNum; ++i)
		for (int j = 0; j < yNum; ++j)
			for (int k = 0; k < zNum; ++k)
				Box[i][j][k] = 0;
	int xPos, yPos, zPos;
	for (int j = 0; j < cloud_ptr->points.size(); ++j){
		xPos = (cloud_ptr->points[j].x - min_x) / _length;
		yPos = (cloud_ptr->points[j].y - min_y) / _length;
		zPos = (cloud_ptr->points[j].z - min_z) / _length;
		Box[xPos][yPos][zPos] += 1;
	}
	for (int i = 0; i < xNum; ++i)
		for (int j = 0; j < yNum; ++j)
			for (int k = 0; k < zNum; ++k){
				if (Box[i][j][k] != 0)
					Ncell += Box[i][j][k];
			}
	for (int i = 0; i < xNum; ++i){
		for (int j = 0; j < yNum; ++j){
			delete[] Box[i][j];
		}
		delete[] Box[i];
	}
	delete[] Box;
	std::cout << "Ncell is " << Ncell << std::endl;
	_Avgdis = _length*sqrtf((float)Ncell / (float)Nall);
	std::cout << "Avgdis is " << _Avgdis << std::endl;
	return _Avgdis;
}

2.边界特征点检测

可以利用点云中点的分布均匀性来判断边界特征点，如图：

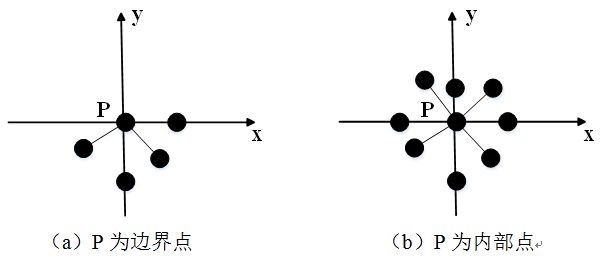
计算待检测数据点P与其邻域点构成的向量之间的夹角并设定最大角度阈值。如果超出阈值则认为其为边界特征点。
这一步可以通过点云库PCL中的BoundaryEstimation类实现，需要设定K近邻搜索的范围和角度阈值。
代码如下，其中cloudOrign是提取边界中使用的原始点云。

pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_b(new pcl::PointCloud<pcl::PointXYZ>);
//计算法线
pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normEst;
pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZ>);
tree->setInputCloud(cloudOrign);
normEst.setInputCloud(cloudOrign);
normEst.setSearchMethod(tree);
normEst.setKSearch(20);
normEst.compute(*normals);
//判断边缘点
pcl::PointCloud<pcl::Boundary> boundaries;
pcl::BoundaryEstimation<pcl::PointXYZ, pcl::Normal, pcl::Boundary> boundEst;
tree2->setInputCloud(cloudOrign);
boundEst.setInputCloud(cloudOrign);
boundEst.setInputNormals(normals);
boundEst.setSearchMethod(tree2);
boundEst.setKSearch(20);    
boundEst.setAngleThreshold(M_PI / 2);
boundEst.compute(boundaries);
//提取边缘点重组点云
cloud_b->width = cloudOrign->points.size();
cloud_b->height = 1;
cloud_b->points.resize(cloud_b->width*cloud_b->height);
int j = 0;
for (int i = 0; i < cloudOrign->points.size(); i++)
	{
	if (boundaries.points[i].boundary_point != 0)
		{
			cloud_b->points[j].x = cloudOrign->points[i].x;
			cloud_b->points[j].y = cloudOrign->points[i].y;
			cloud_b->points[j].z = cloudOrign->points[i].z;
			j++;
		}
		continue;
	}
cloud_b->width = j;
cloud_b->points.resize(cloud_b->width*cloud_b->height);

检测结果如图：

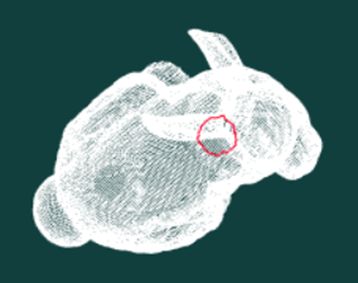
由于检测出的边界点为无需点集还需对其进行排序识别出闭合孔洞，直接依据距离远近连接即可。如果孔洞较小较细密，为了防止孔洞边界之间的误连，可以引入连接走向判断过程，选择偏差角较小的连接点。
闭合孔洞连接结果示意：

3.孔洞修补

修补前需要先对闭合孔洞边界进行预处理。
1.均匀孔洞边界：计算每条边的长度，如果超过2倍平均点距则取其中点加入到孔洞边界中。
2.统一边界方向：将孔洞边界都统一为逆时针方向。
3.内外边界判断：如果点云非全建模，则识别出的闭合孔洞有可能为外部边界轮廓，需要对其进行判断去除。
完成上述三步预处理后即可进入填充点计算。
闭合孔洞边界各顶点的凹凸性不同，夹角计算方式不同，如图：

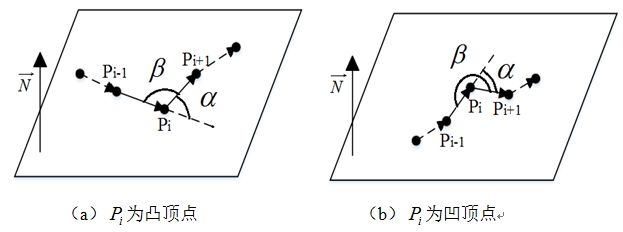
根据计算出各夹角的大小，可以选择以下四种填充方案并更新孔洞多边形，计算得到填充点坐标：
1.夹角小于π/2，不新增填充点，直接更新孔洞多边形。
2.夹角大于π/2，计算新增填充点坐标，以当前判断顶点为圆心，平均点距为半径作圆，作判断点与其左右两边相邻点的中垂线交圆于四点，即夹角开口内部的两个活跃区待填充点为V1和V3。
（1）|V1V3|小于平均点距，取其中点V为填充点，用V替代原判断顶点P。
（2）|V1V3|大于平均点距，小于2倍平均点距，取V1和V3作为填充点，用V1V3替代原判断顶点P。
（3）|V1V3|大于2倍平均点距，取V1和V3作为填充点，但不用其替代原判断顶点P。
如图所示：

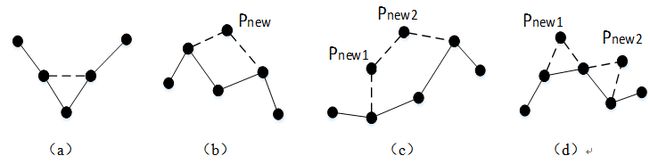
最后需要对于落在孔洞区域外的非法判断点进行去除，即可得到填充点坐标。
反复循环该过程，直至不能计算出新的填充点，则孔洞填充结束。
填充结果如图：

参考文献

[1]顾园园. 散乱点云孔洞修补技术的研究与实现[D]. 苏州：苏州大学，2008.
[2]张丽艳，周儒荣，周来水. 三角网格模型孔洞修补算法研究[J]. 应用科学学报. 2002，20（3）：221-224.