Python计算机视觉编程第三章——图像到图像的映射

图像到图像的映射

（一）单应性变换

定义：单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。在这里，平面是指图像或者三维中的平面表面。单应性变换具有很强的实用性，比如图像配准、 图像纠正和纹理扭曲，以及创建全景图像。我们将频繁地使用单应性变换。本质上， 单应性变换 H，按照下面的方程映射二维中的点（齐次坐标意义下）：

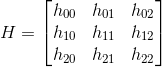
对于图像平面内的点，齐次坐标是个非常有用的表示方式。点的齐次坐标是依赖于其尺度定义的，所以 x=[x,y,w]=[αx,αy,αw]=[x/w,y/w,1] 都表示同一个二维点。因此，单应性矩阵H 也仅依赖尺度定义，所以，单应性矩阵具有 8 个独立的自由度。我们通常使用 w=1 来归 一化点，这样，点具有唯一的图像坐标 x 和 y。这个额外的坐标使得我们可以简单地使用一个矩阵来表示变换。

矩阵H会将一幅图像上的一个点的坐标a=(x,y,1)映射成另一幅图像上的点的坐标b=(x1,y1,1)，也就是说，我们已知a和b，它们是在同一平面上。 则有下面的公式：

即：

得：

得：


对于方程：

可写成一个矩阵与一个向量相乘，即：

其中，

是一个9维的列向量，若令：

则

可记为

这里的

这只是1对点所得到的矩阵A，若有4对点，则得到的矩阵：

由于我们是采用齐次坐标（即(x,y,1)）来表示平面上的点，所以存在一个非零的标量s，使得$b_1$=sH$a^T$与b=sH$a^T$都表示同一个点b。若令

则：

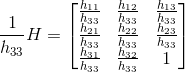
可以看出，其实H只有8个变量（8个自由度）。因此，只需要4个点对，然后通过解线性方程组就可以求得H。也可以多于4个点对。

假设有n≥4个点对，则得到的矩阵：

求解向量h,直接对A进行SVD分解，即

然后取V的最后一列出来作为求解h。因为矩阵A是行满秩，即只有一个自由度。具体实现时，先要得到两幅图，然后在两幅图之间找到4对点的坐标，由此得到矩阵A。

1.1 直接线性变换算法

DLT（Direct Linear Transformation，直接线性变换）是给定４个或者更多对应点对矩阵，来计算单应性矩阵 H 的算法。

我们首先讨论由给定2D到4D的四组点对应

确定H的直接线性算法。变换由方程

给出。注意这是一个齐次矢量方程；因此3维矢量$X_i$’和H$X_i$不相等，它们有相同的方向，但在大小上可能相差一个非零因子。该等式可以用矢量叉乘：

表示，由该表示式可推出H的一个简单线性解。
如果将矩阵H的第j行记为$h^{j}T$，那么：

记

则叉积可以显示地写成：

因为对j=1,2,3,

皆成立，这就给出关于H元素的三个方程，并可以写成下列形式：

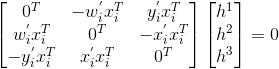
这些方程都有$A_i$h=0的形式，其中$A_i$是3x9的矩阵，h是由矩阵H的元素组成的9维矢量。


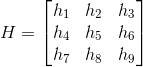
其中$h_i$是h的第i个元素。

求解H：每组点对应给出关于H元素的两个独立的方程。给定四组这样的点对应，便获得方程组 Ah=0，其中A是由每组点对应产生的矩阵行$A_i$构成的方程组的系数矩阵，h是H未知元素的矢量，我们只求h的非零解，因为我们对平凡解h=0毫无兴趣。变换矩阵H一般仅能确定到相差一个尺度，因此解h给出所要求的H。

算法代码如下：

def H_from_points(fp, tp):
    """ Find homography H, such that fp is mapped to tp
        using the linear DLT method. Points are conditioned
        automatically. """

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # condition points (important for numerical reasons)
    # --from points--
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1 / maxstd, 1 / maxstd, 1])
    C1[0][2] = -m[0] / maxstd
    C1[1][2] = -m[1] / maxstd
    fp = dot(C1, fp)

    # --to points--
    m = mean(tp[:2], axis=1)
    maxstd = max(std(tp[:2], axis=1)) + 1e-9
    C2 = diag([1 / maxstd, 1 / maxstd, 1])
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp = dot(C2, tp)

    # create matrix for linear method, 2 rows for each correspondence pair
    nbr_correspondences = fp.shape[1]
    A = zeros((2 * nbr_correspondences, 9))
    for i in range(nbr_correspondences):
        A[2 * i] = [-fp[0][i], -fp[1][i], -1, 0, 0, 0,
                    tp[0][i] * fp[0][i], tp[0][i] * fp[1][i], tp[0][i]]
        A[2 * i + 1] = [0, 0, 0, -fp[0][i], -fp[1][i], -1,
                        tp[1][i] * fp[0][i], tp[1][i] * fp[1][i], tp[1][i]]

    U, S, V = linalg.svd(A)
    H = V[8].reshape((3, 3))

    # decondition
    H = dot(linalg.inv(C2), dot(H, C1))

    # normalize and return
    return H / H[2, 2]

1.2 仿射变换

仿射变换（Affine Transformation或 Affine Map）是一种二维坐标到二维坐标之间的线性变换，它保持了二维图形的“平直性”（即：直线经过变换之后依然是直线）和“平行性”（即：二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变）。

简单来说，仿射变换就是允许图像任意倾斜，而且允许图形在两个方向上任意伸缩变换，但是，不能保持原来的线段长度不变，也不能保持原来的夹角角度不变。

仿射变换可以写为如下的形式：

也可以用矩阵的形式表示如下：

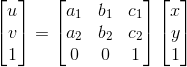
它可以通过一系列原子变换的复合来实现，其中包括平移，缩放，旋转，翻转和错切。不共线的三对对应点决定了一个唯一的仿射变换。

平移：将每一点移到（x’,y’)，变换矩阵为

如果Δx>0，表示图像沿x轴正方向移动；如果Δx<0，表示图像沿x轴负方向移动。
如果Δy>0，表示图像沿y轴正方向移动；如果Δy<0，表示图像沿y轴负方向移动。

平移变换是一种“刚体变换”，rigid-body transformation，就是不会产生形变的理想物体。

缩放变换：将每一点的横坐标放大或缩小$s_x$倍，纵坐标放大(缩小)到$s_y$倍，变换矩阵为

如果Sx>1，则表示在水平方向上放大；如果0 如果Sy>1，则表示在垂直方向上放大；如果0

旋转变换原点：目标图形围绕原点顺时针旋转Θ 弧度，变换矩阵为

旋转变换 ：目标图形以(x,y)为轴心顺时针旋转θ弧度，变换矩阵为

相当于两次平移与一次原点旋转变换的复合，即先将轴心(x,y)移到到原点，然后做旋转变换，最后将图片的左上角置为图片的原点,即

使用对应点对来计算仿射变换矩阵：

def Haffine_from_points(fp, tp):
    """ Find H, affine transformation, such that
        tp is affine transf of fp. """

    if fp.shape != tp.shape:
        raise RuntimeError('number of points do not match')

    # condition points
    # --from points--
    m = mean(fp[:2], axis=1)
    maxstd = max(std(fp[:2], axis=1)) + 1e-9
    C1 = diag([1 / maxstd, 1 / maxstd, 1])
    C1[0][2] = -m[0] / maxstd
    C1[1][2] = -m[1] / maxstd
    fp_cond = dot(C1, fp)

    # --to points--
    m = mean(tp[:2], axis=1)
    C2 = C1.copy()  # must use same scaling for both point sets
    C2[0][2] = -m[0] / maxstd
    C2[1][2] = -m[1] / maxstd
    tp_cond = dot(C2, tp)

    # conditioned points have mean zero, so translation is zero
    A = concatenate((fp_cond[:2], tp_cond[:2]), axis=0)
    U, S, V = linalg.svd(A.T)

    # create B and C matrices as Hartley-Zisserman (2:nd ed) p 130.
    tmp = V[:2].T
    B = tmp[:2]
    C = tmp[2:4]

    tmp2 = concatenate((dot(C, linalg.pinv(B)), zeros((2, 1))), axis=1)
    H = vstack((tmp2, [0, 0, 1]))

    # decondition
    H = dot(linalg.inv(C2), dot(H, C1))

    return H / H[2, 2]

同样地，类似于 DLT 算法，这些点需要经过预处理和去处理化操作。下面， 介绍这些仿射变换是如何处理图像的。

（二）图像扭曲

对图像块应用仿射变换，我们将其称为图像扭曲（或者仿射扭曲）。该操作不仅经常应用在计算机图形学中，而且经常出现在计算机视觉算法中。扭曲操作可以使用 SciPy 工具包中的 ndimage 包来简单完成。命令：

transformed_im = ndimage.affine_transform(im,A,b,size)

编写代码：

# -*- coding: utf-8 -*-
from scipy import ndimage
from PIL import Image
from pylab import *

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

im = array(Image.open('D:\\Python\\chapter3\\jimei.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))

figure()
gray()
subplot(121)
title(u'(a)原始图像', fontproperties=font)
axis('off')
imshow(im)
subplot(122)
title(u'(b)使用 ndimage.affine_transform()函数扭曲后的图像', fontproperties=font)
axis('off')
imshow(im2)
show()

代码运行效果如下：

输出图像结果中丢失的像素用零来补充。

2.1 图像中的图像

仿射扭曲的一个简单例子是，将图像或者图像的一部分放置在另一幅图像中，使得它们能够和指定的区域或者标记物对齐。

将函数 image_in_image() 添加到warp.py文件中。该函数的输入参数为两幅图像和一个坐标。该坐标为将第一幅图像放置到第二幅图像中的角点坐标：

编写代码：

# -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage

# 将im1仿射扭曲到im2的指定位置
im1 = array(Image.open('D:\\Python\\chapter3\\star.jpg').convert('L'))
im2 = array(Image.open('D:\\Python\\chapter3\\road.jpg').convert('L'))
# 选定指定的位置，即目标点
tp = array([[264,538,540,264],[40,36,605,605],[1,1,1,1]])
# 调用的warp.py的image_in_image函数，从而实现仿射变换
im3 = warp.image_in_image(im1, im2, tp)
figure()
gray()
subplot(131)
axis('off')
imshow(im1)
subplot(132)
axis('off')
imshow(im2)
subplot(133)
axis('off')
imshow(im3)
axis('off')
show()

代码运行效果如下：

分析：

将扭曲的图像和第二幅图像融合， 创建 alpha 图像（Alpha是一个8位的灰度图像通道，该通道用256级灰度来记录图像中的透明度信息，定义透明、不透明和半透明区域，其中黑表示透明，白表示不透明，灰表示半透明。）。该图像定义了每个像素从各个图像中获取的像素值成分多少。这里基于以下事实，扭曲的图像是在扭曲区域边界之外以 0 来填充的图像，来创建一个二值的 alpha 图像。严格意义上说，需要在第一幅图像中的潜 在 0 像素上加上一个小的数值，或者合理地处理这些 0 像素。注意，这里使用的图像坐标是齐次坐标意义下的。

2.2 图像配准

图像配准是对图像进行变换，使变换后的图像能够在常见的坐标系中对齐。配准可以是严格配准，也可以是非严格配准。为了能够进行图像对比和更精细的图像分析， 图像配准是一步非常重要的操作。

图像配准可以视为源图像和目标图像关于空间和灰度的映射关系：

f为二维空间坐标变换（如仿射变换），g为一维亮度或其他度量值变换。

图像配准问题的关键：最佳空间变换。
图像配准的实质：不同图像中表征同一位置的物理点一一对应。

配准算法的一般步骤：

1. 特征提取
2. 特征匹配
3. 估计变换模型
4. 图像重采样及变换

（1）特征提取：

特征提取是指分别提取两幅图像中共有的图像特征，这种特征是出现在两幅图像中对比列、旋转、平移等变换保持一致性的特征，如线交叉点、物体边缘角点、虚圆闭区域的中心等可提取的特征。特征包括：点、线和面三类。

点特征是最常用的一种图像特征，包括物体边缘点、角点、线交叉点等；根据各特征点的兴趣值将特征点分成几个等级。对不同的目的，特征点的提取应各有不同。点特征包括下面几种算法：

a. Harris算法
受信号处理中相关函数启发，给出与自相关函数相联系的矩阵M，M矩阵的特征值是自相关函数的一阶曲率，如果两个曲率值都高，那么认为该点就是角点，此方法对图像旋转、亮度变化、视觉变化和噪声的影响具有很好的鲁棒性。




b. Susan算法
susan算法使用一个圆形的模板在图像上滑动，将位于圆形模板中心的待检测的像素点称为核心点。假设图像为非纹理，核心点领域被划分为两个区域：其一为亮度值等于（或相似于）核心点亮度的区域，称为核值相似区，其二为亮度值不相似于核心点亮度的区域。

c. Harris-Laplace算法
Harris算子能最稳定地在图像旋转、光照变化、透视变换条件下提取二维平面特征点，但在三维尺度空间中，Harris探测子的重复探测性能不好，不同尺度Harris特征点存在位置误差，Harris探测子不具有尺度和仿射不变性。而三维尺度空间中最稳定高效的特征尺度探测算子是归一化的Laplace算子。Harris-Laplace的特征点具有尺度和旋转不变得特性，且对光照变换和小范围视角变化具有稳定性。

d. SIFT特征点提取
使用DOG filter来建立尺度空间。在尺度空间上提取极值点。
对于二维函数，其泰勒展开式为：

写成矩阵形式：

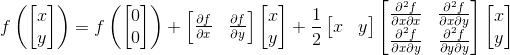
写成向量形式：

其中：

关键点的精确位置就在上式极值点所在位置，对上述式子求导数并令导数为0，则有：

令：

且有：


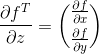
得：


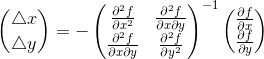
其中f是某一尺度为δ的DoG层。最终得到了△x、△y，即所求极值点相对于关键点的偏移量，若任意一个偏移量超过了0.5，则说明拟合关键点应该在原关键点的相邻位置。在该DoG层不断迭代拟合，确定新关键点位置，直至偏移量都小于0.5（即稳定的关键点）为止。再去除低响应值的点，再删除边缘效应。

e. SURF特征点提取
基于Hessian矩阵，它依靠Hessian矩阵行列式的局部最大值定位兴趣点位置。对于图像I中的某点X在尺度空间上的Hessian矩阵定义为：

其中

表示高斯二阶偏导在X处与图像I的卷积。
     
具有相似含义。

线特征是图像中明显的线段特征，如道路河流的边缘，目标的轮廓线等。线特征的提取一般分两步进行：首先采用某种算法提取出图像中明显的线段信息，然后利用限制条件筛选出满足条件的线段作为线特征。

面特征是指利用图像中明显的区域信息作为特征。在实际的应用中最后可能也是利用区域的重心或圆的圆心点等作为特征。

（ 2 ) 特征匹配

特征匹配分两步
a. 对特征作描述
现有的主要特征描述子：SIFT特征描述子，SURF特征描述子，对比度直方图（CCH）,DAISY特征描述子，矩方法。
b. 利用相似度准则进行特征匹配
常用的相似性测度准则有如欧式距离，马氏距离，Hausdorff距离等。

SIFT特征描述子:
主要思想：一种基于图像梯度分布的特征描述子。
特点：抗干扰性好，但维数高，计算复杂度大。

SURF特征描述子:
主要思想：将特征点的周围区域分成几个子区域，用每个子区域内像素点的x,y方向的偏导及其绝对值的和组成特征点的描述子。
特点：有较好的抗亮度变化能力，但是该描述子要求使用积分图像，限定了其应用范围。

对比度直方图：
主要思想：将特征点周围区域的像素点与特征点的对比度形成直方图来描述该特征点。
特点：该方法比基于梯度的描述子要快。但描述力比基于梯度的要略弱一点。

DAISY特征描述子:
主要思想：受SIFT算法和GLOH算法的启发，将梯度加权和用几个高斯方向偏导滤波器与原图像进行积分代替。
特点：该描述子有和SIFT特征算子相似的优点，但是速度比SIFT特征算子要快。

（3）估计变换模型

空间变换模型是所有配准技术中需要考虑的一个重要因素，各种配准技术都要建立自己的变换模型，变换空间的选取与图像的变形特性有关。常用的空间变换模型有：刚体变换、仿射变换、投影变换、非线性变换。

a.刚体变换模型
缸体变换是平移、旋转与缩放的组合，适用于具有相同视角，但拍摄位置不同的来自同一传感器的两幅图像的配准。刚体变换模型下，若点(x1,y1)，(x2,y2）分别为参考图像和待配准图像中对应的两点，则它们之间满足以下关系：

b.仿射变换模型
如果第一幅图像中的一条直线经过变换后，映射到第二幅图像上仍然为直线，且平行直线仍旧被映射为平行直线，这样的变换称为仿射变换。该变换保持直线间的平行关系，若点(x1,y1) ，(x2,y2)分别为参考图像和待匹配图像中对应的两点，则它们之间满足以下关系：

c.投影变换模型
如果第一幅图像中的一条直线经过变换后，映射到第二幅图像上依然为直线，但平行关系不再保持，则称这样的变换为投影变换。投影变换具有8个参数，可以将成像设备的运动（如平移、旋转、缩放等）描述得更为全面。若点(x1,y1) ，(x2,y2)分别为参考图像和待匹配图像中对应的两点，则它们之间满足以下关系：

d.非线性变换模型
若第一幅图像中的一条直线经变换后，映射到第二幅图像上不再是直线，我们把这样的变换称为非线性变换。在二维空间中，点(x1，y1)经非线性变换至点(x2，y2)变换公式为：

F表示把第一幅图像映射到第二幅图像上的任意一种函数形式。典型的非线性变换如多项式变换，在2D空间中，多项式函数可写成如下形式：


（4）图像重采样及变换

在得到两幅图像的变换参数后，要将输入图像做相应参数的变换，使之与参考图像处于同一坐标系下，则矫正后的输入图像与参考图像可用作后续的图像融合、目标变化检测处理或图像镶嵌；
涉及输入图像变换后所得点坐标不一定为整像素数，则应进行插值处理。常用的插值算法有最近领域法，双线性插值法和立方卷积插值法

配准算法的主要方法

（1） 基于点：

a. SIFT算法
SIFT特征匹配算法包括两个阶段:SIFT特征的生成与SIFT特征向量的匹配。
SIFT特征向量的生成算法包括四步：
1.尺度空间极值检测，以初步确定关键点位置和所在尺度。
2.拟和三维二次函数精确确定位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点。
3.利用关键点领域像素的梯度方向分布特性为每个关键点指定参数方向，使算子具备旋转不变性。
4.生成SIFT特征向量。
SIFT特征向量的匹配
对图像1中的某个关键点，找到其与图像2中欧式距离最近的前两个关键点的距离NN和SCN，如果NN/SCN小于某个比例阈值，则接受这一对匹配点。

b.ASIFT算法
通过原始图像来模拟得到场景在各个视角下的图像，再对这些得到的图像提起SIFT特征点，然后进行匹配。其放射性要好于SIFT，具有全仿射不变性。

c.SUFR算法
特征点提取：
1.计算原图像的积分图像
2.用不同尺寸的框状滤波器来计算不同阶以及不同层上的每个点图像点的行列式。一般计算4阶4层
3.在3维(x,y,S）尺度空间中，在每个3x3x3的局部区域里，进行非最大值抑制。只有比邻近的26个点的响应值都大的点才被选为兴趣点。
特征匹配：
对图像1中的某个关键点，找到其与图像2中欧式距离最近的前两个关键点的距离NN和SCN，如果NN/SCN小于某个比例阈值，则接受这一对匹配点。

（2）基于边缘：

基本思想：用边缘检测算子提取出边缘
边缘匹配：
1.根据边缘的相似度
2.提取边缘上的控制点，如曲率比较大的点等，然后用这些点来进行匹配。
3.将边缘拟合成直线，然后匹配直线。
估计变换参数：用边缘上的控制点或直线的端点，中点等等。

编写代码：
基于SIFT算法的图像配准

# -*- coding: utf-8 -*-
import numpy as np
import cv2

def sift_kp(image):
    gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    sift = cv2.xfeatures2d_SIFT.create()
    kp, des = sift.detectAndCompute(image, None)
    kp_image = cv2.drawKeypoints(gray_image, kp, None)
    return kp_image, kp, des

def get_good_match(des1, des2):
    bf = cv2.BFMatcher()
    matches = bf.knnMatch(des1, des2, k=2)
    good = []
    for m, n in matches:
        if m.distance < 0.75 * n.distance:
            good.append(m)
    return good

def siftImageAlignment(img1, img2):
    _, kp1, des1 = sift_kp(img1)
    _, kp2, des2 = sift_kp(img2)
    goodMatch = get_good_match(des1, des2)
    if len(goodMatch) > 4:
        ptsA = np.float32([kp1[m.queryIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
        ptsB = np.float32([kp2[m.trainIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
        ransacReprojThreshold = 4
        H, status = cv2.findHomography(ptsA, ptsB, cv2.RANSAC, ransacReprojThreshold);
        # 其中H为求得的单应性矩阵矩阵
        # status则返回一个列表来表征匹配成功的特征点。
        # ptsA,ptsB为关键点
        # cv2.RANSAC, ransacReprojThreshold这两个参数与RANSAC有关
        imgOut = cv2.warpPerspective(img2, H, (img1.shape[1], img1.shape[0]),
                                     flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
    return imgOut, H, status

img1 = cv2.imread('D:\\Python\\chapter3\\food3.jpg')
img2 = cv2.imread('D:\\Python\\chapter3\\food6.jpg')
while img1.shape[0] > 1000 or img1.shape[1] > 1000:
    img1 = cv2.resize(img1, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)
while img2.shape[0] > 1000 or img2.shape[1] > 1000:
    img2 = cv2.resize(img2, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_AREA)

result, _, _ = siftImageAlignment(img1, img2)
allImg = np.concatenate((img1, img2, result), axis=1)
cv2.namedWindow('1', cv2.WINDOW_NORMAL)
cv2.namedWindow('2', cv2.WINDOW_NORMAL)
cv2.namedWindow('Result', cv2.WINDOW_NORMAL)
cv2.imshow('1', img1)
cv2.imshow('2', img2)
cv2.imshow('Result', result)
# cv2.imshow('Result',allImg)
if cv2.waitKey(200000) & 0xff == ord('q'):
    cv2.destroyAllWindows()
    cv2.waitKey(1)

代码运行效果如下：



可以看到将图二移动到和图一完全匹配的位置，也就是图三。

基于ASIFT算法的图像配准
编写代码：

# Python 2/3 compatibility
from __future__ import print_function

import numpy as np
import cv2 as cv

# built-in modules
import itertools as it
from multiprocessing.pool import ThreadPool

# local modules
from common import Timer
from find_obj import init_feature, filter_matches, explore_match


def affine_skew(tilt, phi, img, mask=None):
    '''
    affine_skew(tilt, phi, img, mask=None) -> skew_img, skew_mask, Ai

    Ai - is an affine transform matrix from skew_img to img
    '''
    h, w = img.shape[:2]
    if mask is None:
        mask = np.zeros((h, w), np.uint8)
        mask[:] = 255
    A = np.float32([[1, 0, 0], [0, 1, 0]])
    if phi != 0.0:
        phi = np.deg2rad(phi)
        s, c = np.sin(phi), np.cos(phi)
        A = np.float32([[c,-s], [ s, c]])
        corners = [[0, 0], [w, 0], [w, h], [0, h]]
        tcorners = np.int32( np.dot(corners, A.T) )
        x, y, w, h = cv.boundingRect(tcorners.reshape(1,-1,2))
        A = np.hstack([A, [[-x], [-y]]])
        img = cv.warpAffine(img, A, (w, h), flags=cv.INTER_LINEAR, borderMode=cv.BORDER_REPLICATE)
    if tilt != 1.0:
        s = 0.8*np.sqrt(tilt*tilt-1)
        img = cv.GaussianBlur(img, (0, 0), sigmaX=s, sigmaY=0.01)
        img = cv.resize(img, (0, 0), fx=1.0/tilt, fy=1.0, interpolation=cv.INTER_NEAREST)
        A[0] /= tilt
    if phi != 0.0 or tilt != 1.0:
        h, w = img.shape[:2]
        mask = cv.warpAffine(mask, A, (w, h), flags=cv.INTER_NEAREST)
    Ai = cv.invertAffineTransform(A)
    return img, mask, Ai


def affine_detect(detector, img, mask=None, pool=None):
    '''
    affine_detect(detector, img, mask=None, pool=None) -> keypoints, descrs

    Apply a set of affine transformations to the image, detect keypoints and
    reproject them into initial image coordinates.
    See http://www.ipol.im/pub/algo/my_affine_sift/ for the details.

    ThreadPool object may be passed to speedup the computation.
    '''
    params = [(1.0, 0.0)]
    for t in 2**(0.5*np.arange(1,6)):
        for phi in np.arange(0, 180, 72.0 / t):
            params.append((t, phi))

    def f(p):
        t, phi = p
        timg, tmask, Ai = affine_skew(t, phi, img)
        keypoints, descrs = detector.detectAndCompute(timg, tmask)
        for kp in keypoints:
            x, y = kp.pt
            kp.pt = tuple( np.dot(Ai, (x, y, 1)) )
        if descrs is None:
            descrs = []
        return keypoints, descrs

    keypoints, descrs = [], []
    if pool is None:
        ires = it.imap(f, params)
    else:
        ires = pool.imap(f, params)

    for i, (k, d) in enumerate(ires):
        print('affine sampling: %d / %d\r' % (i+1, len(params)), end='')
        keypoints.extend(k)
        descrs.extend(d)

    print()
    return keypoints, np.array(descrs)

if __name__ == '__main__':
    print(__doc__)

    import sys, getopt
    opts, args = getopt.getopt(sys.argv[1:], '', ['feature='])
    opts = dict(opts)
    '''
       --feature:  sift/surf/orb/akaze  
    '''
    feature_name = opts.get('--feature', 'brisk-flann')
    try:
        fn1, fn2 = args
    except:
        fn1 = 'D:\\Python\\chapter3\\building.jpg'
        fn2 = 'D:\\Python\\chapter3\\building2.jpg'

    img1 = cv.imread(fn1, 0)
    img2 = cv.imread(fn2, 0)
    detector, matcher = init_feature(feature_name)

    if img1 is None:
        print('Failed to load fn1:', fn1)
        sys.exit(1)

    if img2 is None:
        print('Failed to load fn2:', fn2)
        sys.exit(1)

    if detector is None:
        print('unknown feature:', feature_name)
        sys.exit(1)
    print('using', feature_name)

    pool = ThreadPool(processes=cv.getNumberOfCPUs())
    kp1, desc1 = affine_detect(detector, img1, pool=pool)
    kp2, desc2 = affine_detect(detector, img2, pool=pool)
    print('img1 - %d features, img2 - %d features' % (len(kp1), len(kp2)))

    def match_and_draw(win):
        with Timer('matching'):
            raw_matches = matcher.knnMatch(desc1, trainDescriptors=desc2, k=2) #2
        p1, p2, kp_pairs = filter_matches(kp1, kp2, raw_matches)
        if len(p1) >= 4:
            H, status = cv.findHomography(p1, p2, cv.RANSAC, 5.0)
            print('%d / %d  inliers/matched' % (np.sum(status), len(status)))
            # do not draw outliers (there will be a lot of them)
            kp_pairs = [kpp for kpp, flag in zip(kp_pairs, status) if flag]
        else:
            H, status = None, None
            print('%d matches found, not enough for homography estimation' % len(p1))
        explore_match(win, img1, img2, kp_pairs, None, H)

    match_and_draw('affine find_obj')
    cv.waitKey()
    cv.destroyAllWindows()

代码运行效果如下：


总结：

当待配准的图像特征十分明显时可以用SURF算法
当待配准的图像特征信息比较弱一些的话可以用SIFT算法
当待配准的图像之间存在较大的视角变换的话可以用ASIFT算法

（三）创建全景图

在同一位置（即图像的照相机位置相同）拍摄的两幅或者多幅图像是单应性相关的 。我们经常使用该约束将很多图像缝补起来，拼成一个大的图像来创建全景图像。

3.1 RANSAC

RANSAC 是“RANdom SAmple Consensus”（随机一致性采样）的缩写。该方法是用来找到正确模型来拟合带有噪声数据的迭代方法。给定一个模型，例如点集之间的单应性矩阵，RANSAC 基本的思想是，数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摒弃噪声点。

RANSAC的基本假设是：
（1）数据由“局内点”组成，例如：数据的分布可以用一些模型参数来解释；
（2）“局外点”是不能适应该模型的数据；
（3）除此之外的数据属于噪声。

局外点产生的原因：噪声的极值；错误的测量方法；对数据的错误假设。

RANSAC也做了以下假设：给定一组（通常很小的）局内点，存在一个可以估计模型参数的过程；而该模型能够解释或者适用于局内点。

RANSAC算法的输入是一组观测数据，一个可以解释或者适应于观测数据的参数化模型，一些可信的参数。
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：

1. 首先我们先随机假设一小组局内点为初始值。然后用此局内点拟合一个模型，此模型适应于假设的局内点，所有的未知参数都能从假设的局内点计算得出。
2. 用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点，将局内点扩充。
3. 如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
4. 然后，用所有假设的局内点去重新估计模型，因为此模型仅仅是在初始的假设的局内点估计的，后续有扩充后，需要更新。
5. 最后，通过估计局内点与模型的错误率来评估模型。

整个这个过程为迭代一次，此过程被重复执行固定的次数，每次产生的模型有两个结局：
1、要么因为局内点太少，还不如上一次的模型，而被舍弃，
2、要么因为比现有的模型更好而被选用。

RANSAC原理
RANSAC目的是找到最优的参数矩阵使得满足该矩阵的数据点个数最多，通常令h33=1来归一化矩阵。由于单应性矩阵有8个未知参数，至少需要8个线性方程求解，对应到点位置信息上，一组点对可以列出两个方程，则至少包含4组匹配点对。

其中(x,y)表示目标图像角点位置，(x’,y’)为场景图像角点位置，s为尺度参数。

RANSAC算法从匹配数据集中随机抽出4个样本并保证这4个样本之间不共线，计算出单应性矩阵，然后利用这个模型测试所有数据，并计算满足这个模型数据点的个数与投影误差(即代价函数)，若此模型为最优模型，则对应的代价函数最小。

RANSAC 的标准例子：用一条直线拟合带有噪声数据的点集。简单的最小二乘在该 例子中可能会失效，但是 RANSAC 能够挑选出正确的点，然后获取能够正确拟合的直线。

编写代码：

import numpy
import scipy  # use numpy if scipy unavailable
import scipy.linalg  # use numpy if scipy unavailable

def ransac(data, model, n, k, t, d, debug=False, return_all=False):
    """fit model parameters to data using the RANSAC algorithm

This implementation written from pseudocode found at
http://en.wikipedia.org/w/index.php?title=RANSAC&oldid=116358182

{{{
Given:
    data - a set of observed data points
    model - a model that can be fitted to data points
    n - the minimum number of data values required to fit the model
    k - the maximum number of iterations allowed in the algorithm
    t - a threshold value for determining when a data point fits a model
    d - the number of close data values required to assert that a model fits well to data
Return:
    bestfit - model parameters which best fit the data (or nil if no good model is found)
iterations = 0
bestfit = nil
besterr = something really large
while iterations < k {
    maybeinliers = n randomly selected values from data
    maybemodel = model parameters fitted to maybeinliers
    alsoinliers = empty set
    for every point in data not in maybeinliers {
        if point fits maybemodel with an error smaller than t
             add point to alsoinliers
    }
    if the number of elements in alsoinliers is > d {
        % this implies that we may have found a good model
        % now test how good it is
        bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
        thiserr = a measure of how well model fits these points
        if thiserr < besterr {
            bestfit = bettermodel
            besterr = thiserr
        }
    }
    increment iterations
}
return bestfit
}}}
"""
    iterations = 0
    bestfit = None
    besterr = numpy.inf
    best_inlier_idxs = None
    while iterations < k:
        maybe_idxs, test_idxs = random_partition(n, data.shape[0])
        maybeinliers = data[maybe_idxs, :]
        test_points = data[test_idxs]
        maybemodel = model.fit(maybeinliers)
        test_err = model.get_error(test_points, maybemodel)
        also_idxs = test_idxs[test_err < t]  # select indices of rows with accepted points
        alsoinliers = data[also_idxs, :]
        if debug:
            print 'test_err.min()', test_err.min()
            print 'test_err.max()', test_err.max()
            print 'numpy.mean(test_err)', numpy.mean(test_err)
            print 'iteration %d:len(alsoinliers) = %d' % (
                iterations, len(alsoinliers))
        if len(alsoinliers) > d:
            betterdata = numpy.concatenate((maybeinliers, alsoinliers))
            bettermodel = model.fit(betterdata)
            better_errs = model.get_error(betterdata, bettermodel)
            thiserr = numpy.mean(better_errs)
            if thiserr < besterr:
                bestfit = bettermodel
                besterr = thiserr
                best_inlier_idxs = numpy.concatenate((maybe_idxs, also_idxs))
        iterations += 1
    if bestfit is None:
        raise ValueError("did not meet fit acceptance criteria")
    if return_all:
        return bestfit, {'inliers': best_inlier_idxs}
    else:
        return bestfit


def random_partition(n, n_data):
    """return n random rows of data (and also the other len(data)-n rows)"""
    all_idxs = numpy.arange(n_data)
    numpy.random.shuffle(all_idxs)
    idxs1 = all_idxs[:n]
    idxs2 = all_idxs[n:]
    return idxs1, idxs2


class LinearLeastSquaresModel:
    """linear system solved using linear least squares

    This class serves as an example that fulfills the model interface
    needed by the ransac() function.

    """

    def __init__(self, input_columns, output_columns, debug=False):
        self.input_columns = input_columns
        self.output_columns = output_columns
        self.debug = debug

    def fit(self, data):
        A = numpy.vstack([data[:, i] for i in self.input_columns]).T
        B = numpy.vstack([data[:, i] for i in self.output_columns]).T
        x, resids, rank, s = numpy.linalg.lstsq(A, B)
        return x

    def get_error(self, data, model):
        A = numpy.vstack([data[:, i] for i in self.input_columns]).T
        B = numpy.vstack([data[:, i] for i in self.output_columns]).T
        B_fit = scipy.dot(A, model)
        err_per_point = numpy.sum((B - B_fit) ** 2, axis=1)  # sum squared error per row
        return err_per_point


def test():
    # generate perfect input data

    n_samples = 500
    n_inputs = 1
    n_outputs = 1
    A_exact = 20 * numpy.random.random((n_samples, n_inputs))
    perfect_fit = 60 * numpy.random.normal(size=(n_inputs, n_outputs))  # the model
    B_exact = scipy.dot(A_exact, perfect_fit)
    assert B_exact.shape == (n_samples, n_outputs)

    # add a little gaussian noise (linear least squares alone should handle this well)
    A_noisy = A_exact + numpy.random.normal(size=A_exact.shape)
    B_noisy = B_exact + numpy.random.normal(size=B_exact.shape)

    if 1:
        # add some outliers
        n_outliers = 100
        all_idxs = numpy.arange(A_noisy.shape[0])
        numpy.random.shuffle(all_idxs)
        outlier_idxs = all_idxs[:n_outliers]
        non_outlier_idxs = all_idxs[n_outliers:]
        A_noisy[outlier_idxs] = 20 * numpy.random.random((n_outliers, n_inputs))
        B_noisy[outlier_idxs] = 50 * numpy.random.normal(size=(n_outliers, n_outputs))

    # setup model

    all_data = numpy.hstack((A_noisy, B_noisy))
    input_columns = range(n_inputs)  # the first columns of the array
    output_columns = [n_inputs + i for i in range(n_outputs)]  # the last columns of the array
    debug = True
    model = LinearLeastSquaresModel(input_columns, output_columns, debug=debug)

    linear_fit, resids, rank, s = numpy.linalg.lstsq(all_data[:, input_columns], all_data[:, output_columns])

    # run RANSAC algorithm
    ransac_fit, ransac_data = ransac(all_data, model,
                                     5, 5000, 7e4, 50,  # misc. parameters
                                     debug=debug, return_all=True)
    if 1:
        import pylab

        sort_idxs = numpy.argsort(A_exact[:, 0])
        A_col0_sorted = A_exact[sort_idxs]  # maintain as rank-2 array

        if 1:
            pylab.plot(A_noisy[:, 0], B_noisy[:, 0], 'k.', label='data')
            pylab.plot(A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'bx',
                       label='RANSAC data')
        else:
            pylab.plot(A_noisy[non_outlier_idxs, 0], B_noisy[non_outlier_idxs, 0], 'k.', label='noisy data')
            pylab.plot(A_noisy[outlier_idxs, 0], B_noisy[outlier_idxs, 0], 'r.', label='outlier data')
        pylab.plot(A_col0_sorted[:, 0],
                   numpy.dot(A_col0_sorted, ransac_fit)[:, 0],
                   label='RANSAC fit')
        pylab.plot(A_col0_sorted[:, 0],
                   numpy.dot(A_col0_sorted, perfect_fit)[:, 0],
                   label='exact system')
        pylab.plot(A_col0_sorted[:, 0],
                   nu  mpy.dot(A_col0_sorted, linear_fit)[:, 0],
                   label='linear fit')
        pylab.legend()
        pylab.show()
if __name__ == '__main__':
    test()

代码运行效果如下：

之所以RANSAC能在有大量噪音情况仍然准确，主要原因是随机取样时只取一部分可以避免估算结果被离群数据影响。

总结:

RANSAC算法的输入为：

1. 观测数据 （包括内群与外群的数据）
2. 符合部分观测数据的模型 （与内群相符的模型）
3. 最少符合模型的内群数量
4. 判断数据是否符合模型的阈值 （数据与模型之间的误差容忍度）
5. 迭代运算次数 （抽取多少次随机内群）

输出为：

1. 最符合数据的模型参数 （如果内群数量小于输入第三条则判断为数据不存在此模型）
2. 内群集 （符合模型的数据）

优点：能在包含大量外群的数据中准确地找到模型参数，并且参数不受到外群影响。
缺点：计算参数时没有一个最大运算时间的顶限，也就是说在迭代次数被限制的情况下，得出来的参数结果有可能并不是最优的，甚至可能不符合真实内群。所以设定 RANSAC参数的时候要根据应用考虑“准确度与效率”哪一个更重要，以此决定做多少次迭代运算。设定与模型的最大误差阈值也是要自己调，因应用而异。还有一点就是RANSAC只能估算一个模型。

3.2 稳健的单应性矩阵估计

我们在任何模型中都可以使用 RANSAC 模块。在使用 RANSAC 模块时，我们只需要在相应 Python 类中实现 fit() 和 get_error() 方法，剩下就是正确地使用 ransac.py，我们这里使用可能的对应点集来自动找到用于全景图像的单应性矩阵。

编写代码：

featname = ['D:\\Python\\chapter3\\building\\building' + str(i + 1) + '.sift' for i in range(5)]
imname = ['D:\\Python\\chapter3\\building\\building' + str(i + 1) + '.jpg' for i in range(5)]

# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

代码运行效果如下：

显然，并不是所有图像中的对应点对都是正确的。实际上，SIFT 是具有很强稳健性的描述子，能够比其他描述子，例如图像块相关的 Harris 角点，产生更少的错误的匹配。但是该方法仍然远非完美。

3.3 拼接图像

创建全景图像步骤大致分为以下几点：

图片之间：

1. 特征点匹配：找到素材图片中共有的图像部分。
2. 图片匹配：连接匹配的特征点，估算图像间几何方面的变换。

全局优化和无缝衔接：

1. 全景图矫直：矫正拍摄图片时相机的相对3D旋转，主要原因是拍摄图片时相机很可能并不在同一水平线上，并且存在不同程度的倾斜，略过这一步可能导致全景图变成波浪形状。
2. 图像均衡补偿：全局平衡所有图片的光照和色调。
3. 图像频段融合：步骤4之后仍然会存在图像之间衔接边缘、晕影效果（图像的外围部分的亮度或饱和度比中心区域低）、视差效果（因为相机透镜移动导致）。

知识储备：

特征点：普遍来讲，一张图片所包含的特征点通常就是周围含有较大信息量的点，而仅通过这些富有特征的局部，基本就可以推测出整张图片。比如说物体的棱角、夜景闪耀的星星，或是图片里的图案和花纹。

在合成全景图的流程里运用的是“点匹配”，也就是匹配局部图片信息。因为局部图片能提取的特征有限，比如说形状特征在这种情况就不适宜，所以一般采用通过整个局部的图案来判断是否符合作为特征的条件。其中运用最普遍的为SIFT特征（Scale-invariant feature transform)，即尺度不变特征转换。 其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。

提取SIFT特征分为两步：侦测与描述（形成特征向量）。简单来讲，侦测就是扫描图片所有的尺度下的所有位置（尺度可以理解为局部缩放）。而判断一个点作为特征点合不合格，需要计算在这个尺度下的高斯差 （DoG，Difference of Gaussians）的局部极值（Local Extrema）。每一个尺度（Scale）下对局部影像进行不同尺度的高斯模糊（局部影像与高斯滤波器的卷积）取差值。局部极值计算，将测试像素的DoG的数值与其26个邻接像素比较取其最大最小极值，也就是测试像素的“特征度” 。

即便找到了特征点，单纯匹配特征点周围的局部影像是行不通的。首先SIFT特征本身最大的优点就是“位置、尺度、旋转不变量"，也就是说在一定范围内旋转或是拉远拉近相机，可以检测出相同的特征点位置（Repeatability）以及提取出相同的特征向量（Scale & Rotation Invariant）， 所以不同角度条件拍摄的图片才可以通过SIFT特征匹配。而像素数值是不具备这些特点的。再者局部影像的像素信息量大导致匹配效率低下。假设这个局部大小 设为16*16像素大小，每一个像素值对应RGB 3个数值，那么每个特征点就对应一个786维的向量（也就是每个点要用786个数表示），考虑到尺度与旋转不变量这个向量又需要乘上十几倍甚至几十倍以覆 盖所有的变化，假设一个图片如果包含上千个特征点，而数据库包含上千张图片，那么在匹配时庞大的计算量无疑是对CPU的一场灾难。

为了保证提取出来的特征向量具有“旋转不变量” 的特性，首先要做的是在每个特征点找到一个“方向”，而这个方向和局部图像的特性应当是一致的，也就是说理想状态下如果旋转这个局部图片，那么重新提取这 个"方向"也和之前相比旋转相同角度。SIFT里选择这个角度的方式是在高斯模糊之后的局部图片里计算每一个像素点的"角度"与"大小"，之后进行投票选 出所有像素最多的那个角度作为主方向。

于是局部图像产生的差值和角度可以通过量化形成特征向量（或称为关键点描述子 - Keypoint Descriptor）。

形成这个向量的方式是"量化"这些角度(比如说把360度平均分成8等分), 然后根据位置累计起来。例如一个8x8的局部采样计算出的2x2的特征矩阵，实际上一般使用的是16x16局部采样形成4x4特征矩阵。所以如果把这个矩阵拉成向量，也就是包含844 = 128个元素。

形成特征向量之后下一个问题就是如何匹配了。 最基本的方式可以称作“最邻近搜索”（Nearest Neighbour），实际上也就是找在128维空间上直线距离最近的的特征向量，这个求直线距离的方式和2维无异，最近的特征向量也就被认为是互相匹配。（知识储备部分感谢博主rlandjon）

接下来的目标就是找到所有匹配(也就是重叠)的图片部分，接连所有图片之后就可以形成一个基本的全景图了。因为每张图片有可能和其他每张图片有重叠部分，所以匹配全部图片需要差不多匹配图片个数的平方次。不过实际上每两张图片之间只需要那么几个相对精准匹配的点就可以估算出这两张图像里的几何关系。

编写代码：

def panorama(H, fromim, toim, padding=2400, delta=2400):
    """ Create horizontal panorama by blending two images
        using a homography H (preferably estimated using RANSAC).
        The result is an image with the same height as toim. 'padding'
        specifies number of fill pixels and 'delta' additional translation. """

    # check if images are grayscale or color
    is_color = len(fromim.shape) == 3

    # homography transformation for geometric_transform()
    def transf(p):
        p2 = dot(H, [p[0], p[1], 1])
        return (p2[0] / p2[2], p2[1] / p2[2])

    if H[1, 2] < 0:  # fromim is to the right
        print ('warp - right')
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim, zeros((toim.shape[0], padding, 3))))
            fromim_t = zeros((toim.shape[0], toim.shape[1] + padding, toim.shape[2]))
            for col in range(3):
                fromim_t[:, :, col] = ndimage.geometric_transform(fromim[:, :, col],
                                                                  transf, (toim.shape[0], toim.shape[1] + padding))
        else:
            # pad the destination image with zeros to the right
            toim_t = hstack((toim, zeros((toim.shape[0], padding))))
            fromim_t = ndimage.geometric_transform(fromim, transf,
                                                   (toim.shape[0], toim.shape[1] + padding))
    else:
        print ('warp - left')
        # add translation to compensate for padding to the left
        H_delta = array([[1, 0, 0], [0, 1, -delta], [0, 0, 1]])
        H = dot(H, H_delta)
        # transform fromim
        if is_color:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0], padding, 3)), toim))
            fromim_t = zeros((toim.shape[0], toim.shape[1] + padding, toim.shape[2]))
            for col in range(3):
                fromim_t[:, :, col] = ndimage.geometric_transform(fromim[:, :, col],
                                                                  transf, (toim.shape[0], toim.shape[1] + padding))
        else:
            # pad the destination image with zeros to the left
            toim_t = hstack((zeros((toim.shape[0], padding)), toim))
            fromim_t = ndimage.geometric_transform(fromim,
                                                   transf, (toim.shape[0], toim.shape[1] + padding))

    # blend and return (put fromim above toim)
    if is_color:
        # all non black pixels
        alpha = ((fromim_t[:, :, 0] * fromim_t[:, :, 1] * fromim_t[:, :, 2]) > 0)
        for col in range(3):
            toim_t[:, :, col] = fromim_t[:, :, col] * alpha + toim_t[:, :, col] * (1 - alpha)
    else:
        alpha = (fromim_t > 0)
        toim_t = fromim_t * alpha + toim_t * (1 - alpha)

    return toim_t

# -*- coding: utf-8 -*-
from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift

"""
This is the panorama example from section 3.3.
"""

# 设置数据文件夹的路径
featname = ['D:\\Python\\chapter3\\building\\building' + str(i + 1) + '.sift' for i in range(5)]
imname = ['D:\\Python\\chapter3\\building\\building' + str(i + 1) + '.jpg' for i in range(5)]

# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化匹配
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配转换成齐次坐标点的函数
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

tp, fp = convert_points(3)  # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3

# 扭曲图像
delta = 2000  # for padding and translation用于填充和平移

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12,im1,im2,delta,delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32,im1,im_02,delta,delta)

im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32,H_43),im1,im_32,delta,2*delta)

figure()
imshow(array(im_42, "uint8"))
axis('off')
show()

代码运行效果如下：

分析：

对于通用的 geometric_transform() 函数，我们需要指定能够描述像素到像素间映射的函数。在这个例子中，transf() 函数就是该指定的函数。该函数通过将像素和 H 相乘，然后对齐次坐标进行归一化来实现像素间的映射。通过查看H 中的平移量， 我们可以决定应该将该图像填补到左边还是右边。当该图像填补到左边时，由于目标图像中点的坐标也变化了，所以在“左边”情况中，需要在单应性矩阵中加入平移。简单起见，我们同样使用 0 像素的技巧来寻找 alpha 图。正如所看到的，图像曝光不同，在单个图像的边界上存在边缘效应。商业的创建全景图像软件里有额外的操作来对强度进行归一化，并对平移进行平滑场景转换，以使得结果看上去更好。