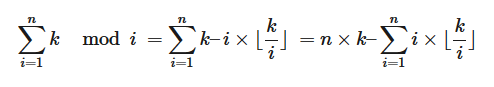数论 分块入门题
例一：bzoj1968: [Ahoi2005]COMMON 约数研究
Description
Input
只有一行一个整数 N（0 < N < 1000000）。
Output
只有一行输出，为整数M，即f(1)到f(N)的累加和。
题目分析
答案即为1..x1..x的所有约数个数和。
我们知道换种形式答案就是∑i⌊ni⌋∑i⌊ni⌋。
那么暴力算法来了：所以我们
for (int i=1; i<=n; i++)
ans += n/i;就好了。
由于n=1e6，所以这个O(n)的算法是能够过去的。但是不行！这个是数论分块的板子题，我们怎么能够止步于O(n)的算法呢？
若用g(i)表示n/i，显然
，并且g(i)是并不严格单调的。
自然而然地想到，在求g(i)的同时能不能够求出[i,j]呢？
这里有一个结论，
，下面来证明这个结论。
我们有
，因此得到 
故jj是满足条件的最大值。
我们要做的就是枚举可能的下整值，并合并计算。
#include
typedef long long ll;
int n;
ll ans;
int main()
{
register int i,j;
scanf("%d",&n);
for (i=1; i<=n; i=j+1)
j = n/(n/i),
ans += 1ll*(j-i+1)*(n/i);
printf("%lld\n",ans);
return 0;
} [CQOI2007]余数求和
来自大佬的证明 https://www.cnblogs.com/five20/p/9199192.html
#include
#include
#include
#define ll long long
using namespace std;
int main()
{
ll n,k;
cin>>n>>k;
ll ans;
ans=n*k;
for(ll i=1,r;i<=n;i=r+1)
{
if(k/i!=0)
r=min(k/(k/i),n);
else// mod 大于n时
r=n;
ans-=(k/i)*(r-i+1)*(i+r)/2;
}
cout< BZOJ2956 (模积和)
Description
求∑∑((n mod i)*(m mod j))其中1<=i<=n,1<=j<=m,i≠j。
Input
第一行两个数n,m。
Output
一个整数表示答案mod 19940417的值
Sample Input
3 4
Sample Output
1
样例说明
答案为(3 mod 1)*(4 mod 2)+(3 mod 1) * (4 mod 3)+(3 mod 1) * (4 mod 4) + (3 mod 2) * (4 mod 1) + (3 mod 2) * (4 mod 3) + (3 mod 2) * (4 mod 4) + (3 mod 3) * (4 mod 1) + (3 mod 3) * (4 mod 2) + (3 mod 3) * (4 mod 4) = 1数据规模和约定
对于100%的数据n,m<=10^9。
#include
#include
#include
#define ll long long
using namespace std;
const ll mod=19940417;
//inv(2)=9970209 inv(6)=3323403;
ll sum(ll n)// n*(n+1)*(2*n+1)/6 完全平方数 求和公式
{
return n*(n+1)%mod*(2*n+1)%mod*3323403%mod;
}
ll solve(ll m,ll n)
{
ll res=0;
for(int i=1,r;i<=m;i=r+1)
{
r=min(m,n/(n/i));
res+=(n/i)*(r-i+1)%mod*(i+r)%mod*9970209%mod;
res%=mod;
}
return res;
}
int main()
{
ll n,m;
cin>>n>>m;
ll ans1,ans2;
ll p=min(n,m);
ans1=(n*n%mod-solve(n,n)%mod)%mod;
ans2=(m*m%mod-solve(m,m)%mod)%mod;
ll ans3=p*n%mod*m%mod-solve(p,n)*m%mod-solve(p,m)*n%mod;
ans3=(ans3+mod)%mod;
for(ll i=1,r;i<=p;i=r+1)
{
r=min(p,min(n/(n/i),m/(m/i)));
ans3+=(n/i)*(m/i)%mod*((sum(r)-sum(i-1))%mod)%mod;
ans3%=mod;
}
cout<<((ans1*ans2-ans3)%mod+mod)%mod<