并查集的实现
一、结构
并查集由一群集合构成，最开始时所有元素各自单独构成一个集合。比如，有一批元素arr = [a, b, c, d, e]，我们需要将这一批元素初始化成单个元素的集合，即a单独构成一个集合，b单独构成一个集合。其中并查集中的单个集合结构如下所示：
当集合中只有一个元素时，这个元素的father为自己，也就是这个集合的代表节点。当一个集合有多个节点时，代表节点为集合中某节点的father指向其自己的节点，比如下图的节点a。
我们使用哈希表来保存所有并查集所有集合的所有元素的father信息，记为fatherMap。比如，哈希表fatherMap中的某一条记录会为(当前节点，father节点)。也就是key为当前节点，而value为当前节点的father节点。
另外，我们使用另外一个哈希表rankMap来保存一个集合中的元素个数，即集合的大小rank。且只有一个集合的代表节点的rank信息才有效。rankMap的某条记录为（代表节点，集合节点数）。上图中集合的rank为6，并记录在代表节点a对应的valuer中。
二、查找
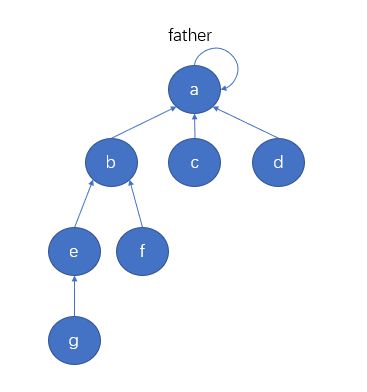
在并查集中，若要查找一个节点属于哪个集合，就是在查这个节点所在集合的代表节点是什么，一个节点通过father信息逐渐找到最上面的节点，其中某个节点的father是自己本身，那么这个节点即为代表节点，也代表整个集合。比如下图中，节点g和节点c所在的集合的代表节点同为节点a，那么这两个节点同为一个集合，否则不是。
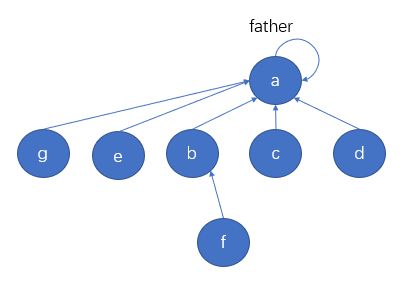
通过一个节点找到所在集合代表节点的过程叫作findFather过程，findFather最终会返回代表节点，但在查找过程会把整个查找路径压缩。比如再进行findFather(g)的过程中，会将查找路径的节点g, e, b的father都设置为a，则集合会变成如下图所示的样子。
三、合并
接下来介绍集合的合并。首先，两个集合进行合并操作时，参数并不是两个集合，而是并查集中的任意两个节点，记为a和b。所以集合的合并更准确的说法是，根据a找到a所在集合的代表节点是findFather(a)，记为aF，b同理为bF。合并过程如下：
- 如果aF == bF，说明a和b本身就在一个集合里，不用合并；
- 如果aF != bF，那么从rankMap中获取代表节点aF和bF所处集合的节点数，分别为aFRank和bFRank。如果aFRank > bFRank，那么将节点b所处的集合合并到节点a所处的集合中，其中代表节点bF的father设置为节点aF，并修改aFRank的值为aFRank + bFRank。而bF的rank信息可以删除，因为已经不会再次使用到了。aFRank < bFRank的情况同理，而aFRank == bFRank的情况我们可以假定与aFRank > bFRank的情况一样。
四、实现
并查集所有代码见如下的UnionFindSet类实现。
import java.util.HashMap;
import java.util.List;
class Element<T> {
public T val;
public Element(T val) {
this.val = val;
}
}
public class UnionFindSet<T> {
private HashMap<Element<T>, Element<T>> fatherMap;
private HashMap<Element<T>, Integer> rankMap;
public UnionFindSet(List<Element<T>> eles) {
makeSets(eles);
}
private void makeSets(List<Element<T>> eles) {
fatherMap = new HashMap<>();
rankMap = new HashMap<>();
//构建单元素并查集合
for (Element<T> el : eles) {
fatherMap.put(el, el);
rankMap.put(el, 1);
}
}
//查找元素所处集合的代表节点并压缩查找路径
public Element<T> findFather(Element<T> e) {
Element<T> father = fatherMap.get(e);
if (e != father) {
father = findFather(father);
}
fatherMap.put(e, father);
return father;
}
//合并集合
public void union(Element<T> a, Element<T> b) {
if (a == null || b == null) return;
Element<T> aF = findFather(a);
Element<T> bF = findFather(b);
if (aF != bF) {
int aFRank = rankMap.get(aF);
int bFRank = rankMap.get(bF);
if (aFRank >= bFRank) {
fatherMap.put(bF, aF);
rankMap.put(aF, aFRank + bFRank);
} else {
fatherMap.put(aF, bF);
rankMap.put(bF, aFRank + bFRank);
}
}//if
}
public boolean isSameSet(Element<T> a, Element<T> b) {
return findFather(a) == findFather(b);
}
}
五、岛问题扩展
我们先了解一下岛问题。
一个矩阵中只有0和1两种值， 每个位置都可以和自己的上、 下、 左、 右四个位置相连， 如果有一片1连在一起， 这个部分叫做一个岛。
举例：
这个矩阵中有三个岛。
复杂岛问题的求解可以利用并查集来实现，比如有如下矩阵（实际可以是很大的矩阵）。
由于矩阵过于大，一台机器计算岛数量会过慢。因此假设我们将矩阵分为两个部分，可以将两个子矩阵分由两台机器并发执行计算得出各自的岛数量，得出的总数量为4，然后再计算大矩阵实际的岛数量为2。
问题是我们如何通过子矩阵计算大矩阵实际的岛数量呢？观察下图，首先，我们在计算左边子矩阵的岛数量时，首先会从a从右然后在往下走，然后将这些节点合并为一个并查集，其中第一个节点1（a所指向的节点，后面我们用a, b, c, d代称代表节点）为代表节点，其他三个到同理。
经过上述过程我们知道岛1元素集合的代表节点为a，岛2元素集合的代表节点为b，岛3元素集合的代表节点为c，岛4元素集合的代表节点为d。下面我们考虑两个子矩阵的边界元素。
观察下图，现在我们只考虑子矩阵的边界元素。 假设现在指针在遍历边界元素时指向如下，发现黑色指针所指向的元素为1，且其右边的蓝色指针指向的元素也是1。那么又发现左边的节点所属集合的代表节点为a，而右边的节点所属集合的代表节点为b，此时将代表节点b所属的集合合并到集合a中，并将上次计算各子矩阵岛数量的总和num减1，即num = 4 - 1 = 3。
黑色和蓝色指针都向往下移动一位，此时会发现两指针指向的元素所属同一个集合，因此num值不变。
两指针继续往下移动，假设现在某一时刻指针的指向如下图所示：
我们发现黑色指针指向的元素属于代表节点为c的集合，而蓝色指针指向的元素属于代表节点为a的集合，此时集合不相等，num再次减1变为2，同时在将两集合合并。经过上述步骤最终得出实际的岛数量2。
在遇到大矩阵时，我们完全可以将大矩阵拆分为多个子矩阵并交由多台机器去计算各自的岛数量，同时利用并查集完成最后实际岛数量的计算。
本文参考《程序员代码面试指南—IT名企算法与数据结构题目最优解》