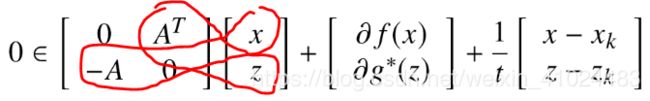最优化方法 25:PDHG
前面的章节要么从原始问题出发,要么从对偶问题出发,通过求解近似点或者一个子优化问题进行迭代,而且推导过程中我们发现根据问题的参数特征,比如矩阵 A A A 是瘦高型的还是矮胖型的,采用对偶和原始问题的复杂度会不一样,可以选择一个更简单的。而这一节,我们将要从原始对偶问题出发来优化,什么是原始对偶问题呢?就是原始优化变量和对偶优化变量(原始函数和共轭函数)混合在一块,看下面的原理就知道了。
1. 原始对偶问题
现在考虑原始优化问题,其中 f , g f,g f,g 为闭凸函数
min f ( x ) + g ( A x ) \min \quad f(x)+g(Ax) minf(x)+g(Ax)
这个问题我们前面遇到好多次了,一般都是取 y = A x y=Ax y=Ax 加一个约束条件然后计算拉格朗日函数(自己拿小本本写一下),再求解 KKT 条件对吧。好,让我们列出来 KKT 条件:
- 原始可行性: x ∈ dom f , A x = y ∈ dom g x\in\text{dom}f,Ax=y\in\text{dom}g x∈domf,Ax=y∈domg
- x , z x,z x,z 是拉格朗日函数的最小值点,因此 − A T z ∈ ∂ f ( x ) , z ∈ ∂ g ( y ) -A^Tz\in\partial f(x),z\in\partial g(y) −ATz∈∂f(x),z∈∂g(y)
其中 z ∈ ∂ g ( y ) ⟺ A x = y ∈ ∂ g ⋆ ( z ) z\in\partial g(y)\iff Ax=y\in\partial g^\star(z) z∈∂g(y)⟺Ax=y∈∂g⋆(z)。也就是说,要想求解 KKT 条件,我们需要的实际上是求解下面一个“方程”
0 ∈ [ 0 A T − A 0 ] [ x z ] + [ ∂ f ( x ) ∂ g ⋆ ( z ) ] 0 \in\left[\begin{array}{cc}0 & A^{T} \\-A & 0\end{array}\right]\left[\begin{array}{l}x \\z\end{array}\right]+\left[\begin{array}{c}\partial f(x) \\\partial g^{\star}(z)\end{array}\right] 0∈[0−AAT0][xz]+[∂f(x)∂g⋆(z)]
Remarks:这个式子可重要啦,后面还会用到!而且他从集合的角度揭示了我们求解最优值问题的本质,那就是找一个包含关系。
比如上面的这个式子我们用一个算子来表示为 T ( x , z ) T(x,z) T(x,z),我们求解最优值实际上要就是找满足 0 ∈ T ( x , z ) 0\in T(x,z) 0∈T(x,z) 的解 ( x ⋆ , z ⋆ ) (x^\star,z^\star) (x⋆,z⋆)。而对一个简单的优化问题 min f ( x ) \min f(x) minf(x),我们实际上就是在找满足 0 ∈ ∂ f ( x ) 0\in\partial f(x) 0∈∂f(x) 的 x ⋆ x^\star x⋆,这个时候我们可以把次梯度看作是一个算子。
在这一章的后面几个小节,我们将从算子的角度重新来看待优化问题,看完之后可以再回到这里细细品味。
好我们先把这个东西放一放,再来看看另一个跟拉格朗日函数有关的函数
h ( x , z ) = inf y L ( x , y , z ) = f ( x ) − g ⋆ ( z ) + z T A x \begin{aligned} h(x,z)&=\inf_{y}L(x,y,z)\\ &=f(x)-g^\star(z)+z^TAx \end{aligned} h(x,z)=yinfL(x,y,z)=f(x)−g⋆(z)+zTAx
如果计算 0 ∈ ∂ h ( x , z ) 0\in\partial h(x,z) 0∈∂h(x,z) 是不是就是上面那个方程?!也就是说上面很重要的那个方程实际上就是在求解 h ( x , z ) h(x,z) h(x,z) 的鞍点!很容易理解,因为 KKT 条件本质上就是在求拉格朗日函数的鞍点(当然,如果存在不等式约束就不一定是鞍点了)。大家注意,你看这个 h h h 他又长又宽,这个 h h h 同时包含了原始变量 x x x 和对偶变量 z z z,同时还既有原始函数 f f f 又有对偶函数 g ⋆ g^\star g⋆,所以我们叫他原始对偶优化问题, h h h 也是部分拉格朗日函数(partial Lagrangian)。
2. PDHG
前面说了我们要求解的问题是
0 ∈ [ 0 A T − A 0 ] [ x z ] + [ ∂ f ( x ) ∂ g ⋆ ( z ) ] 0 \in\left[\begin{array}{cc} 0 & A^{T} \\ -A & 0 \end{array}\right]\left[\begin{array}{l} x \\ z \end{array}\right]+\left[\begin{array}{c} \partial f(x) \\ \partial g^{\star}(z) \end{array}\right] 0∈[0−AAT0][xz]+[∂f(x)∂g⋆(z)]
**PDHG(Primal-dual hybrid gradient method)**的迭代格式是这样的
x k + 1 = prox τ f ( x k − τ A T z k ) z k + 1 = prox σ g ∗ ( z k + σ A ( 2 x k + 1 − x k ) ) \begin{array}{l} x_{k+1}=\operatorname{prox}_{\tau f}\left(x_{k}-\tau A^{T} z_{k}\right) \\ z_{k+1}=\operatorname{prox}_{\sigma g^{*}}\left(z_{k}+\sigma A\left(2 x_{k+1}-x_{k}\right)\right) \end{array} xk+1=proxτf(xk−τATzk)zk+1=proxσg∗(zk+σA(2xk+1−xk))
步长需要满足 σ τ ∥ A ∥ 2 2 ≤ 1 \sigma\tau\|A\|_2^2\le1 στ∥A∥22≤1。
是不是看起来跟 DR 方法很像呢?事实上他们两个是等价的,后面会证明。回忆 ADMM,我们每次需要求解的优化问题是
x k + 1 = arg min x f ( x ) + t 2 ∥ A x − y k + z k t ∥ 2 x^{k+1}=\arg\min_x f(x)+\frac{t}{2}\| Ax-y^k+\frac{z^k}{t}\|^2 xk+1=argxminf(x)+2t∥Ax−yk+tzk∥2
要求解这个优化问题,我们往往会得到一个线性方程,还需要计算 ( A T A ) − 1 (A^TA)^{-1} (ATA)−1,这就很麻烦了。但是观察 PDHG 的迭代格式,我们只需要求解 f , g ⋆ f,g^\star f,g⋆ 的 prox \text{prox} prox 算子,我们只需要求解 A , A T A,A^T A,AT 之间的乘法而不需要求逆了,这就方便很多了。
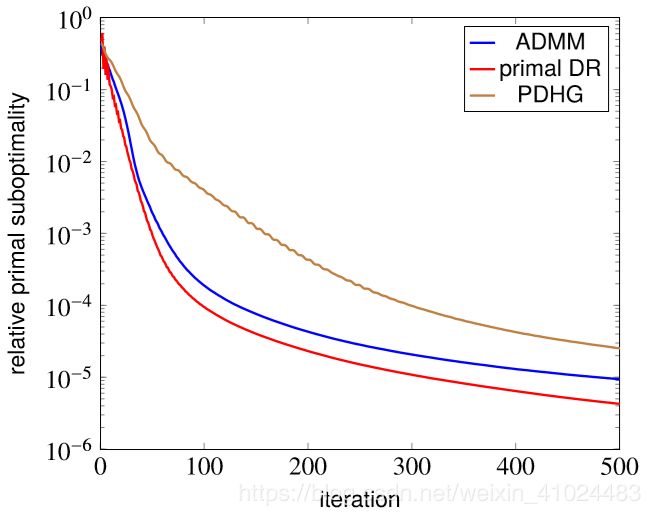
看上面这个例子,我们前面说过 ADMM 等价于 dual DR,不过这个例子里边 PDHG 是最慢的。
下面我们就来证明一下如何从 PDHG 导出 DR 方法。
对于优化问题 min f ( x ) + g ( x ) \min f(x)+g(x) minf(x)+g(x),实际上相当于 min f ( x ) + g ( A x ) , A = I \min f(x)+g(Ax),A=I minf(x)+g(Ax),A=I,另外我们再取 PDHG 中的 σ = τ = 1 \sigma=\tau=1 σ=τ=1,那么就可以得到
x k + 1 = prox f ( x k − z k ) z k + 1 = prox g ∗ ( z k + 2 x k + 1 − x k ) \begin{array}{l} x_{k+1}=\operatorname{prox}_{f}\left(x_{k}-z_{k}\right) \\ z_{k+1}=\operatorname{prox}_{g^{*}}\left(z_{k}+2 x_{k+1}-x_{k}\right) \end{array} xk+1=proxf(xk−zk)zk+1=proxg∗(zk+2xk+1−xk)
这实际上就是 DR Splitting 那一节讲的原始对偶形式。
另外也可以从 DR 方法导出 PDHG。我们可以将原问题 min f ( x ) + g ( A x ) \min f(x)+g(A x) minf(x)+g(Ax) 改写为
minimize f ( x ) + g ( A x + B y ) subject to y = 0 \begin{aligned} \operatorname{minimize} &\quad f(x)+g(A x+B y) \\ \text{subject to} &\quad y=0 \end{aligned} minimizesubject tof(x)+g(Ax+By)y=0
这里边我们可以选择 B B B 使 A A T + B B T = ( 1 / α ) I AA^T+BB^T=(1/\alpha)I AAT+BBT=(1/α)I,其中 1 / α ≥ ∥ A ∥ 2 2 1/\alpha\ge\|A\|_2^2 1/α≥∥A∥22。为什么这么选呢?令
g ~ ( x , y ) = g ( A x + B y ) = g ( A ~ ( x y ) ) \tilde{g}(x,y)=g(Ax+By)=g\left(\tilde{A}\left(\begin{array}{c}x\\ y\end{array}\right)\right) g~(x,y)=g(Ax+By)=g(A~(xy))
那么就有 A ~ A ~ T = ( 1 / α ) I \tilde{A}\tilde{A}^T=(1/\alpha)I A~A~T=(1/α)I,而前面讲 prox \text{prox} prox 算子的时候我们讲了一个性质,满足这个条件的时候 prox g ~ \text{prox}_{\tilde{g}} proxg~ 可以用 prox g \text{prox}_g proxg 来表示。
复习: prox \text{prox} prox 算子的性质
f ( x ) = g ( A x + b ) f(x)=g(Ax+b) f(x)=g(Ax+b),对于一般的 A A A 并不能得到比较好的性质,但如果 A A T = ( 1 / α ) I AA^T=(1/\alpha)I AAT=(1/α)I,则有
prox f ( x ) = ( I − α A T A ) x + α A T ( prox α − 1 g ( A x + b ) − b ) = x − α A T ( A x + b − prox α − 1 g ( A x + b ) ) \begin{aligned}\operatorname{prox}_{f}(x) &=\left(I-\alpha A^{T} A\right) x+\alpha A^{T}\left(\operatorname{prox}_{\alpha^{-1} g}(A x+b)-b\right) \\&=x-\alpha A^{T}\left(A x+b-\operatorname{prox}_{\alpha^{-1} g}(A x+b)\right)\end{aligned} proxf(x)=(I−αATA)x+αAT(proxα−1g(Ax+b)−b)=x−αAT(Ax+b−proxα−1g(Ax+b))
我们还可以取 f ~ ( x , y ) = f ( x ) + δ 0 ( y ) \tilde{f}(x,y)=f(x)+\delta_{0}(y) f~(x,y)=f(x)+δ0(y),那么优化问题就变成了 min f ~ ( x , y ) + g ~ ( x , y ) \min \tilde{f}(x,y)+\tilde{g}(x,y) minf~(x,y)+g~(x,y),应用 DR 方法迭代格式为
[ x k + 1 y k + 1 ] = prox τ f ~ ( [ x k − p k y k − q k ] ) [ p k + 1 q k + 1 ] = prox ( τ g ~ ) ∗ ( [ p k + 2 x k + 1 − x k q k + 2 y k + 1 − y k ] ) \begin{array}{l} {\left[\begin{array}{c} x_{k+1} \\ y_{k+1} \end{array}\right]=\operatorname{prox}_{\tau \tilde{f}} \left(\left[\begin{array}{c} x_{k}-p_{k} \\ y_{k}-q_{k} \end{array}\right]\right)} \\ {\left[\begin{array}{c} p_{k+1} \\ q_{k+1} \end{array}\right]=\operatorname{prox}_{(\tau \tilde{g})^{*}}\left(\left[\begin{array}{c} p_{k}+2 x_{k+1}-x_{k} \\ q_{k}+2 y_{k+1}-y_{k} \end{array}\right]\right)} \end{array} [xk+1yk+1]=proxτf~([xk−pkyk−qk])[pk+1qk+1]=prox(τg~)∗([pk+2xk+1−xkqk+2yk+1−yk])
我们需要计算 prox f ~ \text{prox}_{\tilde{f}} proxf~ 和 prox g ~ \text{prox}_{\tilde{g}} proxg~
prox τ f ~ ( x , y ) = [ prox τ f ( x ) 0 ] prox τ g ~ ( x , y ) = [ x y ] − α [ A T B T ] ( A x + B y − prox ( τ / α ) g ( A x + B y ) = [ x y ] − τ [ A T B T ] prox σ g ⋆ ( σ ( A x + B y ) ) = [ x y ] − prox ( τ g ~ ) ⋆ ( x , y ) \operatorname{prox}_{\tau \tilde{f}}(x, y)=\left[\begin{array}{c} \operatorname{prox}_{\tau f}(x) \\ 0 \end{array}\right] \\ \begin{aligned} \operatorname{prox}_{\tau \tilde{g}}(x, y) &=\left[\begin{array}{c} x \\ y \end{array}\right]-\alpha\left[\begin{array}{c} A^{T} \\ B^{T} \end{array}\right]\left(A x+B y-\operatorname{prox}_{(\tau / \alpha) g}(A x+B y)\right.\\ &=\left[\begin{array}{c} x \\ y \end{array}\right]-\tau\left[\begin{array}{c} A^{T} \\ B^{T} \end{array}\right] \operatorname{prox}_{\sigma g^{\star}}(\sigma(A x+B y)) \\ &=\left[\begin{array}{c} x \\ y \end{array}\right]-\operatorname{prox}_{(\tau \tilde{g})^\star}(x, y) \end{aligned} proxτf~(x,y)=[proxτf(x)0]proxτg~(x,y)=[xy]−α[ATBT](Ax+By−prox(τ/α)g(Ax+By)=[xy]−τ[ATBT]proxσg⋆(σ(Ax+By))=[xy]−prox(τg~)⋆(x,y)
其中 σ = α / τ \sigma=\alpha/\tau σ=α/τ。代入到 DR 方法的迭代方程
[ x k + 1 y k + 1 ] = [ prox τ f ( x k − p k ) 0 ] [ p k + 1 q k + 1 ] = τ [ A T B T ] prox σ g ∗ ( σ [ A B ] [ p k + 2 x k + 1 − x k q k + 2 y k + 1 − y k ] ) \begin{array}{l} {\left[\begin{array}{c} x_{k+1} \\ y_{k+1} \end{array}\right]=\left[\begin{array}{c} \operatorname{prox}_{\tau f}\left(x_{k}-p_{k}\right) \\ 0 \end{array}\right]} \\ {\left[\begin{array}{c} p_{k+1} \\ q_{k+1} \end{array}\right]=\tau\left[\begin{array}{c} A^{T} \\ B^{T} \end{array}\right] \operatorname{prox}_{\sigma g^{*}}\left(\sigma\left[\begin{array}{cc} A & B \end{array}\right]\left[\begin{array}{c} p_{k}+2 x_{k+1}-x_{k} \\ q_{k}+2 y_{k+1}-y_{k} \end{array}\right]\right)} \end{array} [xk+1yk+1]=[proxτf(xk−pk)0][pk+1qk+1]=τ[ATBT]proxσg∗(σ[AB][pk+2xk+1−xkqk+2yk+1−yk])
根据第二个式子应该有 [ p k q k ] ∈ range [ A T B T ] \left[\begin{array}{c} p_{k} \\ q_{k} \end{array}\right] \in \text { range }\left[\begin{array}{c} A^{T} \\ B^{T} \end{array}\right] [pkqk]∈ range [ATBT],因此存在 z k z_k zk 满足 [ p k + 1 q k + 1 ] = τ [ A T B T ] z k \left[\begin{array}{c}p_{k+1} \\ q_{k+1}\end{array}\right]=\tau\left[\begin{array}{c}A^{T} \\ B^{T}\end{array}\right]z_k [pk+1qk+1]=τ[ATBT]zk。同时因为 A A T + B B T = ( 1 / α ) I AA^T+BB^T=(1/\alpha)I AAT+BBT=(1/α)I,所以能找到唯一的 z k z_k zk 同时满足 z k = σ ( A p k + B q k ) z_k=\sigma(Ap_k+Bq_k) zk=σ(Apk+Bqk)。那么把 z k z_k zk 代入到上面的迭代方程,同时消掉 y k = 0 y_k=0 yk=0,就可以得到
x k + 1 = prox τ f ( x k − τ A T z k ) z k + 1 = prox σ g ∗ ( z k + σ A ( 2 x k + 1 − x k ) ) x_{k+1}=\operatorname{prox}_{\tau f}\left(x_{k}-\tau A^{T} z_{k}\right)\\ z_{k+1}=\operatorname{prox}_{\sigma g^{*}}\left(z_{k}+\sigma A\left(2 x_{k+1}-x_{k}\right)\right) xk+1=proxτf(xk−τATzk)zk+1=proxσg∗(zk+σA(2xk+1−xk))
这就是 PDHG 算法,其中 σ τ = α ≤ 1 / ∥ A ∥ 2 \sigma\tau=\alpha\le 1/\|A\|^2 στ=α≤1/∥A∥2。
当然,我们还可以对 PDHG 算法进行改进,比如:
PDHG withover relaxation: ρ k ∈ ( 0 , 2 ) \rho_k\in(0,2) ρk∈(0,2)
x ˉ k + 1 = prox τ f ( x k − τ A T z k ) z ˉ k + 1 = prox σ g ∗ ( z k + σ A ( 2 x ˉ k + 1 − x k ) ) [ x k + 1 z k + 1 ] = [ x k z k ] + ρ k [ x ˉ k + 1 − x k z ˉ k + 1 − z k ] \begin{aligned} \bar{x}_{k+1} &=\operatorname{prox}_{\tau f}\left(x_{k}-\tau A^{T} z_{k}\right) \\ \bar{z}_{k+1} &=\operatorname{prox}_{\sigma g^{*}}\left(z_{k}+\sigma A\left(2 \bar{x}_{k+1}-x_{k}\right)\right) \\ \left[\begin{array}{c} x_{k+1} \\ z_{k+1} \end{array}\right] &=\left[\begin{array}{c} x_{k} \\ z_{k} \end{array}\right]+\rho_{k}\left[\begin{array}{c} \bar{x}_{k+1}-x_{k} \\ \bar{z}_{k+1}-z_{k} \end{array}\right] \end{aligned} xˉk+1zˉk+1[xk+1zk+1]=proxτf(xk−τATzk)=proxσg∗(zk+σA(2xˉk+1−xk))=[xkzk]+ρk[xˉk+1−xkzˉk+1−zk]
其收敛性与 DR 方法相同。
PDHG with acceleration:
x k + 1 = prox τ k f ( x k − τ k A T z k ) z k + 1 = prox σ k g ∗ ( z k + σ k A ( ( 1 + θ k ) x k + 1 − θ k x k ) ) \begin{array}{l} x_{k+1}=\operatorname{prox}_{\tau_{k} f}\left(x_{k}-\tau_{k} A^{T} z_{k}\right) \\ z_{k+1}=\operatorname{prox}_{\sigma_{k} g^{*}}\left(z_{k}+\sigma_{k} A\left(\left(1+\theta_{k}\right) x_{k+1}-\theta_{k} x_{k}\right)\right) \end{array} xk+1=proxτkf(xk−τkATzk)zk+1=proxσkg∗(zk+σkA((1+θk)xk+1−θkxk))
对于强凸函数 f f f,以及适当的选择 σ k , τ k , θ k \sigma_k,\tau_k,\theta_k σk,τk,θk,收敛速度可以达到 1 / k 2 1/k^2 1/k2。
3. 单调算子
单调算子(monotone operator)我们在讲次梯度的时候提到过,这次我们从算子的角度理解一下 PDHG 方法。
3.1 集值算子
集值算子(Multivalued/set-valued operator),就是说映射得到的不是单个的值,而是一个集合。比如算子 F F F 把向量 x ∈ R n x\in R^n x∈Rn 映射到集合 F ( x ) ⊆ R n F(x)\subseteq R^n F(x)⊆Rn。有两个定义
- 定义域 dom F = { x ∈ R n ∣ F ( x ) ≠ ∅ } \operatorname{dom} F =\left\{x \in \mathbf{R}^{n} | F(x) \neq \emptyset\right\} domF={x∈Rn∣F(x)=∅}
- 图 gr ( F ) = { ( x , y ) ∈ R n × R n ∣ x ∈ dom F , y ∈ F ( x ) } \operatorname{gr}(F) =\left\{(x, y) \in \mathbf{R}^{n} \times \mathbf{R}^{n} | x \in \operatorname{dom} F, y \in F(x)\right\} gr(F)={(x,y)∈Rn×Rn∣x∈domF,y∈F(x)}
对算子放缩、求逆等操作都可以表示为对“图”的线性变换。
求逆: F − 1 ( x ) = { y ∣ x ∈ F ( y ) } F^{-1}(x)=\{y| x\in F(y)\} F−1(x)={y∣x∈F(y)}
gr ( F − 1 ) = [ 0 I I 0 ] gr ( F ) \operatorname{gr}\left(F^{-1}\right)=\left[\begin{array}{cc} 0 & I \\ I & 0 \end{array}\right] \operatorname{gr}(F) gr(F−1)=[0II0]gr(F)
放缩: ( λ F ) ( x ) = λ F ( x ) (\lambda F)(x)=\lambda F(x) (λF)(x)=λF(x) and ( F λ ) ( x ) = F ( λ x ) (F\lambda)(x)=F(\lambda x) (Fλ)(x)=F(λx)
gr ( λ F ) = [ I 0 0 λ I ] gr ( F ) , gr ( F λ ) = [ ( 1 / λ ) I 0 0 I ] gr ( F ) \operatorname{gr}(\lambda F)=\left[\begin{array}{cc} I & 0 \\ 0 & \lambda I \end{array}\right] \operatorname{gr}(F), \quad \operatorname{gr}(F \lambda)=\left[\begin{array}{cc} (1 / \lambda) I & 0 \\ 0 & I \end{array}\right] \operatorname{gr}(F) gr(λF)=[I00λI]gr(F),gr(Fλ)=[(1/λ)I00I]gr(F)
相加: ( I + λ F ) ( x ) = { x + λ y ∣ y ∈ F ( x ) } (I+\lambda F)(x)=\{x+\lambda y | y \in F(x)\} (I+λF)(x)={x+λy∣y∈F(x)}
gr ( I + λ F ) = [ I 0 I λ I ] gr ( F ) \operatorname{gr}(I+\lambda F)=\left[\begin{array}{cc} I & 0 \\ I & \lambda I \end{array}\right] \operatorname{gr}(F) gr(I+λF)=[II0λI]gr(F)
注意 ( I + λ F ) (I+\lambda F) (I+λF) 这个形式很特别,如果我们取 F ( x ) = ∂ f ( x ) F(x)=\partial f(x) F(x)=∂f(x),那么 ( I + λ F ) − 1 (I+\lambda F)^{-1} (I+λF)−1 实际上就是 prox \text{prox} prox 算子( λ > 0 \lambda>0 λ>0),不过我们给他取了另一个名字 Resolvent, y ∈ ( I + λ F ) − 1 ( x ) ⟺ x − y ∈ ∂ f ( y ) y\in(I+\lambda F)^{-1}(x)\iff x-y\in\partial f(y) y∈(I+λF)−1(x)⟺x−y∈∂f(y),用图来表示就是
gr ( ( I + λ F ) − 1 ) = [ I λ I I 0 ] gr ( F ) \operatorname{gr}\left((I+\lambda F)^{-1}\right)=\left[\begin{array}{cc} I & \lambda I \\ I & 0 \end{array}\right] \operatorname{gr}(F) gr((I+λF)−1)=[IIλI0]gr(F)
例子 1: ( I + λ ∂ f ( x ) ) − 1 = prox λ f ( x ) (I+\lambda \partial f(x))^{-1}=\text{prox}_{\lambda f}(x) (I+λ∂f(x))−1=proxλf(x)
例子 2: F ( x ) = A x + b F(x)=Ax+b F(x)=Ax+b, ( I + λ F ) − 1 ( x ) = ( I + λ A ) − 1 ( x − λ b ) (I+\lambda F)^{-1}(x)=(I+\lambda A)^{-1}(x-\lambda b) (I+λF)−1(x)=(I+λA)−1(x−λb),后面这个求逆完全就是矩阵求逆。
3.2 单调算子
定义: F F F 是单调算子,若
( y − y ^ ) T ( x − x ^ ) ≥ 0 for all x , x ^ ∈ dom F , y ∈ F ( x ) , y ^ ∈ F ( x ^ ) (y-\hat{y})^{T}(x-\hat{x}) \geq 0 \quad \text { for all } x, \hat{x} \in \operatorname{dom} F, y \in F(x), \hat{y} \in F(\hat{x}) (y−y^)T(x−x^)≥0 for all x,x^∈domF,y∈F(x),y^∈F(x^)
如果用图表示,就应该有
[ x − x ^ y − y ^ ] T [ 0 I I 0 ] [ x − x ^ y − y ^ ] ≥ 0 for all ( x , y ) , ( x ^ , y ^ ) ∈ gr ( F ) ( ★ ) \left[\begin{array}{c}x-\hat{x} \\y-\hat{y}\end{array}\right]^{T}\left[\begin{array}{cc}0 & I \\I & 0\end{array}\right]\left[\begin{array}{c}x-\hat{x} \\y-\hat{y}\end{array}\right] \geq 0 \quad \text { for all }(x, y),(\hat{x}, \hat{y}) \in \operatorname{gr}(F) \quad (\bigstar) [x−x^y−y^]T[0II0][x−x^y−y^]≥0 for all (x,y),(x^,y^)∈gr(F)(★)
上面这个式子很重要!!!后面会多次用到。
例子:我们需要用到的单调算子有:
- 凸函数次梯度 ∂ f ( x ) \partial f(x) ∂f(x)
- 仿射变换 F ( x ) = C x + d F(x)=Cx+d F(x)=Cx+d,并且需要满足 C + C T ⪰ 0 C+C^T\succeq 0 C+CT⪰0
- 他们的组合,比如
F ( x , z ) = [ 0 A T − A 0 ] [ x z ] + [ ∂ f ( x ) ∂ g ∗ ( z ) ] F(x, z)=\left[\begin{array}{cc} 0 & A^{T} \\ -A & 0 \end{array}\right]\left[\begin{array}{c} x \\ z \end{array}\right]+\left[\begin{array}{c} \partial f(x) \\ \partial g^{*}(z) \end{array}\right] F(x,z)=[0−AAT0][xz]+[∂f(x)∂g∗(z)]
除了单调算子,还有个最大单调算子(Maximal monotone operator),也就是说它的图不能是其他任意单调算子的真子集,举个栗子就明白了,参考下面的图。我们可以知道b闭凸函数的偏导数、单调仿射变换是最大单调算子,除此之外,还有定理。
Minty’s Theorem:单调算子 F F F 是最大单调算子当且仅当
im ( I + F ) = ⋃ x ∈ dom F ( x + F ( x ) ) = R n \operatorname{im}(I+F)=\bigcup_{x \in \operatorname{dom} F}(x+F(x))=\mathbf{R}^{n} im(I+F)=x∈domF⋃(x+F(x))=Rn
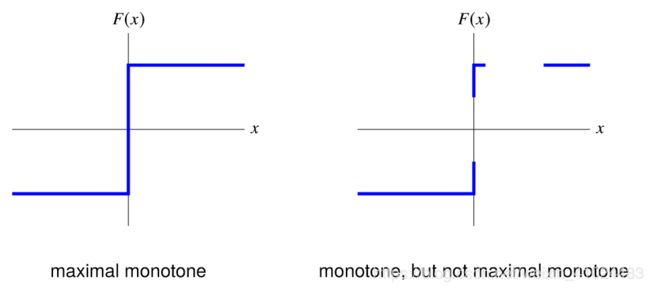
除了单调性质,我们在证明收敛新的时候往往还要用到 Lipschitz 连续、强凸性质等等,实际上我们前面已经介绍过很多次了,而且用了一堆名词 coercivity、expansive、firmly nonexpansive,我实在是晕了…这里我们就再总结一下。假设算子 F F F 有 y = F ( x ) , y ^ = F ( x ^ ) y=F(x),\hat{y}=F(\hat{x}) y=F(x),y^=F(x^)
| ( y − y ^ ) T ( x − x ^ ) ≥ μ ∥ x − x ^ ∥ 2 , μ > 0 (y-\hat{y})^T(x-\hat{x})\ge \mu \| x-\hat{x}\|^2,\mu>0 (y−y^)T(x−x^)≥μ∥x−x^∥2,μ>0 | ( y − y ^ ) T ( x − x ^ ) ≥ γ ∥ y − y ^ ∥ 2 , γ > 0 (y-\hat{y})^T(x-\hat{x})\ge \gamma \|y-\hat{y}\|^2,\gamma>0 (y−y^)T(x−x^)≥γ∥y−y^∥2,γ>0 | ( y − y ^ ) T ( x − x ^ ) ≤ L ∥ x − x ^ ∥ 2 (y-\hat{y})^T(x-\hat{x})\le L\|x-\hat{x}\|^2 (y−y^)T(x−x^)≤L∥x−x^∥2 |
|---|---|---|
| coercive | co-coercive | |
| firmly nonexpansive( γ = 1 \gamma=1 γ=1) | nonexpansive( L ≤ 1 L\le 1 L≤1) | |
| Lipschitz continuous |
它们之间的关系
- 如果满足 co-coercive 并且有 γ = 1 \gamma=1 γ=1,则其为 firmly nonexpansive
- 如果满足 Lipschitz continuous 并且有 L ≤ 1 L\le 1 L≤1,则其为 nonexpansive
- co-coercivity 可以导出 Lipschitz continuous( L = 1 / γ L=1/\gamma L=1/γ),但反之不一定。不过对于闭凸函数他们是等价的。
它们各自的性质
Coercivity等价于 F − μ I F-\mu I F−μI 是一个单调算子,也等价于
[ x − x ^ y − y ^ ] T [ − 2 μ I I I 0 ] [ x − x ^ y − y ^ ] ≥ 0 for all ( x , y ) , ( x ^ , y ^ ) ∈ gr ( F ) \left[\begin{array}{c} x-\hat{x} \\ y-\hat{y} \end{array}\right]^{T}\left[\begin{array}{cc} -2 \mu I & I \\ I & 0 \end{array}\right]\left[\begin{array}{c} x-\hat{x} \\ y-\hat{y} \end{array}\right] \geq 0 \quad \text { for all }(x, y),(\hat{x}, \hat{y}) \in \operatorname{gr}(F) [x−x^y−y^]T[−2μIII0][x−x^y−y^]≥0 for all (x,y),(x^,y^)∈gr(F)
Co-coercivity等价于
[ x − x ^ y − y ^ ] T [ 0 I I − 2 γ I ] [ x − x ^ y − y ^ ] ≥ 0 for all ( x , y ) , ( x ^ , y ^ ) ∈ gr ( F ) \left[\begin{array}{c} x-\hat{x} \\ y-\hat{y} \end{array}\right]^{T}\left[\begin{array}{cc} 0 & I \\ I & -2 \gamma I \end{array}\right]\left[\begin{array}{c} x-\hat{x} \\ y-\hat{y} \end{array}\right] \geq 0 \quad \text { for all }(x, y),(\hat{x}, \hat{y}) \in \operatorname{gr}(F) [x−x^y−y^]T[0II−2γI][x−x^y−y^]≥0 for all (x,y),(x^,y^)∈gr(F)
对前面提到的 resolvent 来说,算子单调性有以下重要性质:
重要性质:算子是单调的,当且仅当他的 resolvant 是 firmly nonexpansive
证明只需要根据矩阵等式 λ [ 0 I I 0 ] = [ I I λ I 0 ] [ 0 I I − 2 I ] [ I λ I I 0 ] \lambda\left[\begin{array}{ll}0 & I \\ I & 0\end{array}\right]=\left[\begin{array}{cc}I & I \\ \lambda I & 0 \end{array}\right]\left[\begin{array}{cc}0 & I \\ I & -2 I \end{array}\right]\left[\begin{array}{cc}I & \lambda I \\ I & 0 \end{array}\right] λ[0II0]=[IλII0][0II−2I][IIλI0] 就可以得到(结合 ( ★ ) (\bigstar) (★) 式)。
另外单调算子 F F F 是最大单调算子,当且仅当
dom ( I + λ F ) − 1 = R n \text{dom}(I+\lambda F)^{-1}=R^n dom(I+λF)−1=Rn
这可以由 Minty’s theorem 得到。
4. 近似点算法
4.1 回望 PPA
前面讲到了 Resolvant ( I + λ F ) − 1 (I+\lambda F)^{-1} (I+λF)−1 实际上就是近似点算子,而 PPA 就是在计算近似点,回忆 PPA 的迭代格式为
x k + 1 = prox t k f ( x k ) = ( 1 + t k F ) − 1 ( x k ) \begin{aligned} x_{k+1} &= \text{prox}_{t_k f}(x_k) \\ &= (1+t_k F)^{-1}(x_k) \end{aligned} xk+1=proxtkf(xk)=(1+tkF)−1(xk)
我们实际上就是在找 Resolvant 算子 R t = ( I + t F ) − 1 R_t=(I+t F)^{-1} Rt=(I+tF)−1 的不动点
x = R t ( x ) ⟺ x ∈ ( 1 + t F ) ( x ) ⟺ 0 ∈ F ( x ) x=R_t(x)\iff x\in(1+tF)(x)\iff 0\in F(x) x=Rt(x)⟺x∈(1+tF)(x)⟺0∈F(x)
加入松弛后的 PPA 可以写成下面的形式,其中 ρ k ∈ ( 0 , 2 ) \rho_k\in(0,2) ρk∈(0,2) 为松弛参数
x k + 1 = x k + ρ k ( R t k ( x k ) − x k ) x_{k+1}=x_k+\rho_k(R_{t_k}(x_k)-x_k) xk+1=xk+ρk(Rtk(xk)−xk)
那么收敛性是怎么样呢?假如 F − 1 ( 0 ) ≠ ∅ F^{-1}(0)\neq \varnothing F−1(0)=∅,在满足以下条件时 PPA 可以收敛
- t k = t > 0 , ρ k = ρ ∈ ( 0 , 2 ) t_k=t>0,\rho_k=\rho\in(0,2) tk=t>0,ρk=ρ∈(0,2) 都选择常数值;或者
- t k , ρ k t_k,\rho_k tk,ρk 随迭代次数变化,但是需要满足 t k ≥ t min > 0 , 0 < ρ min ≤ ρ k ≤ ρ max < 2 , ∀ k t_k\ge t_{\min}> 0,0<\rho_{\min}\le \rho_k\le \rho_{\max}< 2,\forall k tk≥tmin>0,0<ρmin≤ρk≤ρmax<2,∀k
这个收敛性的证明可以通过证明 Resolvant 的 firmly nonexpansiveness 性质来完成(可以去复习 DR 方法的收敛性证明,那里实际上也是一个不动点迭代)。
4.2 再看 PPA
先打个预防针,这一部分很重要!!!看完以后也许会对 PPA 以及其他优化算法有更多的理解!!!
首先我们回忆 PPA 是什么。对于优化问题 min f ( x ) \min f(x) minf(x),迭代格式为 x + = prox t f ( x ) x^+=\text{prox}_{tf}(x) x+=proxtf(x)。如果我们把 ∂ f ( x ) \partial f(x) ∂f(x) 用算子 F F F 来表示,那么优化问题实际上就是在找满足 0 ∈ F ( x ) 0\in F(x) 0∈F(x) 的解,PPA 实际上就是在找不动点 x = ( 1 + t F ) − 1 ( x ) x=(1+tF)^{-1}(x) x=(1+tF)−1(x)。
假如我们现在引入一个非奇异矩阵 A A A,令 x = A y x=Ay x=Ay 代入到原方程(为什么要这么做?如果合适地选择 A A A 的话,有时候可以使问题简化,跟着推导的思路看到最后就能理解了,来吧!)
记 g ( y ) = f ( A y ) g(y)=f(Ay) g(y)=f(Ay),那么优化问题变为了 min g ( y ) \min g(y) ming(y),注意由于 A A A 是非奇异的,所以这个问题跟原问题 min f ( x ) \min f(x) minf(x) 是等价的。我们需要找满足 0 ∈ ∂ g ( y ) = A T ∂ f ( A y ) 0\in\partial g(y)=A^T\partial f(Ay) 0∈∂g(y)=AT∂f(Ay) 的解,于是可以定义算子 G ( y ) = ∂ g ( y ) = A T F ( A y ) G(y)=\partial g(y)=A^TF(Ay) G(y)=∂g(y)=ATF(Ay),这个时候 G G G 的图就是做一个线性变换
gr ( G ) = [ A − 1 0 0 A T ] gr ( F ) \operatorname{gr}(G)=\left[\begin{array}{cc}A^{-1} & 0 \\0 & A^{T}\end{array}\right] \operatorname{gr}(F) gr(G)=[A−100AT]gr(F)
如果 F F F 是一个单调算子的话,那么 G G G 也是一个单调算子,这是因为(结合 ( ★ ) (\bigstar) (★) 式)
[ A − 1 0 0 A T ] T [ 0 I I 0 ] [ A − 1 0 0 A T ] = [ 0 I I 0 ] \left[\begin{array}{cc}A^{-1} & 0 \\0 & A^{T}\end{array}\right]^{T}\left[\begin{array}{cc}0 & I \\I & 0\end{array}\right]\left[\begin{array}{cc}A^{-1} & 0 \\0 & A^{T}\end{array}\right]=\left[\begin{array}{cc}0 & I \\I & 0\end{array}\right] [A−100AT]T[0II0][A−100AT]=[0II0]
然后对 min g ( y ) \min g(y) ming(y) 应用 PPA 迭代格式为
y k + 1 = ( I + t k G ) − 1 ( y k ) y_{k+1}=(I+t_kG)^{-1}(y_k) yk+1=(I+tkG)−1(yk)
我们把 x k = A y k , G = A T F ( A y ) x_k=Ay_k,G=A^TF(Ay) xk=Ayk,G=ATF(Ay) 都代入进去,就能把上面的式子等价表示为
1 t k H ( x k − x ) ∈ F ( x ) \frac{1}{t_k}H(x_k-x)\in F(x) tk1H(xk−x)∈F(x)
其中 H = ( A A T ) − 1 ≻ 0 H=(AA^T)^{-1}\succ 0 H=(AAT)−1≻0。这个式子又可以表示为
x k + 1 = ( H + t k F ) − 1 ( H x k ) x_{k+1}=(H+t_kF)^{-1}(Hx_k) xk+1=(H+tkF)−1(Hxk)
因为 min g ( y ) ⟺ min f ( x ) \min g(y)\iff \min f(x) ming(y)⟺minf(x),所以上面这个迭代格式也完全适用于原问题,如果取 H = I H=I H=I 那就是原始形式的 PPA,如果取别的形式,那么就获得了推广形式的 PPA!
引入 A A A 有什么作用呢?我们看
1 t k H ( x k − x ) ∈ F ( x ) ⟺ x k + 1 = arg min x ( f ( x ) + 1 2 t k ∥ x − x k ∥ H 2 ) \frac{1}{t_k}H(x_k-x)\in F(x) \iff x_{k+1}=\arg\min_x\left(f(x)+\frac{1}{2t_k}\|x-x_k\|_H^2 \right) tk1H(xk−x)∈F(x)⟺xk+1=argxmin(f(x)+2tk1∥x−xk∥H2)
其中 ∥ x ∥ H 2 = x T H x \|x\|_H^2=x^THx ∥x∥H2=xTHx,如果说 f ( x ) = ( 1 / 2 ) ∥ B x − b ∥ 2 f(x)=(1/2)\|Bx-b\|^2 f(x)=(1/2)∥Bx−b∥2,那么我们就可以选择 A A A 使 H = ( 1 / α ) I − B T B H=(1/\alpha) I-B^TB H=(1/α)I−BTB,这样迭代求解 x k + 1 x_{k+1} xk+1 就简单了。当然这个作用范围很有限,下面的例子更能显现他的威力。
我们再回到原始对偶问题,记算子 F F F 为
F ( x , z ) = [ 0 A T − A 0 ] [ x z ] + [ ∂ f ( x ) ∂ g ⋆ ( z ) ] F(x,z)=\left[\begin{array}{cc}0 & A^{T} \\-A & 0\end{array}\right]\left[\begin{array}{l}x \\z\end{array}\right]+\left[\begin{array}{c}\partial f(x) \\\partial g^{\star}(z)\end{array}\right] F(x,z)=[0−AAT0][xz]+[∂f(x)∂g⋆(z)]
优化问题就是要找到 0 ∈ F ( x , z ) 0\in F(x,z) 0∈F(x,z)。如果用原始的 PPA 算法,迭代方程为 ( x k + 1 , z k + 1 ) = ( I + t F ) − 1 ( x k , z k ) (x_{k+1},z_{k+1})=(I+tF)^{-1}(x_k,z_k) (xk+1,zk+1)=(I+tF)−1(xk,zk), ( x k + 1 , z k + 1 ) (x_{k+1},z_{k+1}) (xk+1,zk+1) 是下面方程的解
注意到 x , z x,z x,z 纠缠在一起了,我们想把他们拆开来分别求解 x , z x,z x,z,问题就能更简单。怎么做呢,引入一个 H H H
H = [ I − τ A T − τ A ( τ / σ ) I ] H=\left[\begin{array}{cc}I & -\tau A^{T} \\-\tau A & (\tau / \sigma) I\end{array}\right] H=[I−τA−τAT(τ/σ)I]
其中若 σ τ ∥ A ∥ 2 2 < 1 \sigma\tau\|A\|_2^2< 1 στ∥A∥22<1 则 H H H 为正定矩阵。这个时候 ( x k + 1 , z k + 1 ) (x_{k+1},z_{k+1}) (xk+1,zk+1) 就是下面方程的解
1 I − τ A T τ − τ A ( τ / σ ) I ] [ x k − x z k − z ] ∈ [ 0 A T − A 0 ] [ x z ] + [ ∂ f ( x ) ∂ g ∗ ( z ) ] ⇕ 0 ∈ ∂ f ( x ) + 1 τ ( x − x k + τ A T z k ) 0 ∈ ∂ g ∗ ( z ) + 1 σ ( z − z k − σ A ( 2 x − x k ) ) ⇕ x k + 1 = ( I + τ ∂ f ) − 1 ( x k − τ A T z k ) z k + 1 = ( I + σ ∂ g ∗ ) − 1 ( z k + σ A ( 2 x k + 1 − x k ) ) \left.\begin{array}{c|cc}1 & I & -\tau A^{T} \\\tau & -\tau A & (\tau / \sigma) I\end{array}\right]\left[\begin{array}{c}x_{k}-x \\z_{k}-z\end{array}\right] \in\left[\begin{array}{cc}0 & A^{T} \\-A & 0\end{array}\right]\left[\begin{array}{c}x \\z\end{array}\right]+\left[\begin{array}{c}\partial f(x) \\\partial g^{*}(z)\end{array}\right] \\\Updownarrow \\\begin{array}{l}0 \in \partial f(x)+\frac{1}{\tau}\left(x-x_{k}+\tau A^{T} z_{k}\right) \\0 \in \partial g^{*}(z)+\frac{1}{\sigma}\left(z-z_{k}-\sigma A\left(2 x-x_{k}\right)\right)\end{array} \\\Updownarrow \\\begin{aligned}x_{k+1} &=(I+\tau \partial f)^{-1}\left(x_{k}-\tau A^{T} z_{k}\right) \\z_{k+1} &=\left(I+\sigma \partial g^{*}\right)^{-1}\left(z_{k}+\sigma A\left(2 x_{k+1}-x_{k}\right)\right)\end{aligned} 1τI−τA−τAT(τ/σ)I][xk−xzk−z]∈[0−AAT0][xz]+[∂f(x)∂g∗(z)]⇕0∈∂f(x)+τ1(x−xk+τATzk)0∈∂g∗(z)+σ1(z−zk−σA(2x−xk))⇕xk+1zk+1=(I+τ∂f)−1(xk−τATzk)=(I+σ∂g∗)−1(zk+σA(2xk+1−xk))
对于化简后的式子,我们就可以先单独求解 x k + 1 x_{k+1} xk+1,然后再求解 z k + 1 z_{k+1} zk+1。这实际上也是 PDHG 的迭代方程
x k + 1 = prox τ f ( x k − τ A T z k ) z k + 1 = prox σ g ∗ ( z k + σ A ( 2 x k + 1 − x k ) ) \begin{array}{l}x_{k+1}=\operatorname{prox}_{\tau f}\left(x_{k}-\tau A^{T} z_{k}\right) \\z_{k+1}=\operatorname{prox}_{\sigma g^{*}}\left(z_{k}+\sigma A\left(2 x_{k+1}-x_{k}\right)\right)\end{array} xk+1=proxτf(xk−τATzk)zk+1=proxσg∗(zk+σA(2xk+1−xk))
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
最优化方法 15:梯度方法
最优化方法 16:次梯度
最优化方法 17:次梯度下降法
最优化方法 18:近似点算子 Proximal Mapping
最优化方法 19:近似梯度下降
最优化方法 20:对偶近似点梯度下降法
最优化方法 21:加速近似梯度下降方法
最优化方法 22:近似点算法 PPA
最优化方法 23:算子分裂法 & ADMM
最优化方法 24:ADMM
最优化方法 25:PDHG