最优化方法 26:不动点迭代
前面讲了很多具体的算法,比如梯度、次梯度、近似点梯度、加速近似点梯度、PPA、DR方法、ADMM、ALM等,对这些方法的迭代过程有了一些了解。这一节则主要是针对算法的收敛性进行分析,试图从一个更加抽象的层面,利用不动点迭代的思想,把上面的算法综合起来,给一个比较 general 的收敛性分析方法。
1. 什么是不动点?
对于希尔伯特空间(Hilbert space) H \mathcal{H} H,定义了内积 < ⋅ , ⋅ > \left<\cdot,\cdot\right> ⟨⋅,⋅⟩ 和 范数 ∥ ⋅ ∥ \|\cdot\| ∥⋅∥(可以借助于 R 2 \R^2 R2 来想象)。算子 T : H → H T:\mathcal{H}\to\mathcal{H} T:H→H(或者是 C → C C\to C C→C, C C C 为 H \mathcal{H} H 的闭子集)。那么算子 T T T 的不动点集合就定为
F i x T : = { x ∈ H : x = T ( x ) } \mathrm{Fix} T:=\{x \in \mathcal{H}: x=T(x)\} FixT:={x∈H:x=T(x)}
如果不动点集合非空,想要研究的是不动点迭代 x k + 1 ← T ( x k ) x^{k+1}\leftarrow T(x^k) xk+1←T(xk) 的收敛性。为了简便,常把 T ( x ) T(x) T(x) 写为 T x Tx Tx。
为什么要研究不动点迭代呢?因为前面我们讲的算法里面很多都可以表示为这种形式。
例子 1(GD) :对于无约束优化 min f ( x ) \min f(x) minf(x),不假设 f f f 一定是凸的。如果有 ∇ f ( x ⋆ ) = 0 \nabla f(x^\star)=0 ∇f(x⋆)=0,那么 x ⋆ x^\star x⋆ 被称为驻点(stationary point)。梯度下降做的什么事呢? x k + 1 = x k − γ ∇ f ( x k ) x^{k+1}=x^k-\gamma \nabla f(x^k) xk+1=xk−γ∇f(xk),所以实际上算子 T T T 为
T : = I − γ ∇ f T:=I-\gamma \nabla f T:=I−γ∇f
我们要找的最优解 x ⋆ x^\star x⋆ 满足 ∇ f ( x ⋆ ) = 0 ⟹ x ⋆ = T ( x ⋆ ) \nabla f(x^\star)=0\Longrightarrow x^\star=T(x^\star) ∇f(x⋆)=0⟹x⋆=T(x⋆),因此我们要找的就是 T T T 的不动点。
例子 2(PG1) :对于有约束优化 min f ( x ) , s.t. x ∈ C \min f(x),\text{ s.t. }x\in C minf(x), s.t. x∈C,假设 f f f 为正常的闭凸函数, C C C 为非空闭凸集。对于这个带约束的优化问题,我们可以做完一步梯度下降以后再做个投影 x k + 1 ← proj C ( x k − γ ∇ f ( x k ) ) x^{k+1}\leftarrow \operatorname{proj}_{C}(x^k-\gamma \nabla f(x^k)) xk+1←projC(xk−γ∇f(xk)),所以有
T : = proj C ( I − γ ∇ f ) T:=\operatorname{proj}_{C}(I-\gamma \nabla f) T:=projC(I−γ∇f)
而我们要找的最优解需要满足 ⟨ ∇ f ( x ⋆ ) , x − x ⋆ ⟩ ≥ 0 ∀ x ∈ C ⟺ 0 ∈ ∇ f ( x ⋆ ) + ∂ δ C ( x ⋆ ) \left\langle\nabla f\left(x^{\star}\right), x-x^{\star}\right\rangle \geq 0 \quad \forall x \in C \iff 0\in \nabla f(x^\star)+\partial \delta_C(x^\star) ⟨∇f(x⋆),x−x⋆⟩≥0∀x∈C⟺0∈∇f(x⋆)+∂δC(x⋆),这实际上还是在找 T T T 的不动点。
例子 3(PG2) :上面向 C C C 的投影实际上也是在算 prox \text{prox} prox 算子。对于优化问题 min f ( x ) + g ( x ) \min f(x)+g(x) minf(x)+g(x) 我们要解的方程是
0 ∈ ∇ f ( x ) + ∂ g ( x ) ⟺ 0 ∈ x + ∇ f ( x ) − x + ∂ g ( x ) ⟺ ( I − ∇ f ) ( x ) ∈ ( I + ∂ g ) ( x ) ⟺ x = ( I + ∂ g ) − 1 ( I − ∇ f ) ( x ) \begin{array}{c} 0\in \nabla f(x)+\partial g(x) \iff 0\in x+\nabla f(x)-x+\partial g(x) \\ \iff (I-\nabla f)(x)\in (I+\partial g)(x) \\ \iff x=(I+\partial g)^{-1}(I-\nabla f)(x) \end{array} 0∈∇f(x)+∂g(x)⟺0∈x+∇f(x)−x+∂g(x)⟺(I−∇f)(x)∈(I+∂g)(x)⟺x=(I+∂g)−1(I−∇f)(x)
上一节讲到了 ( I + ∂ g ) − 1 (I+\partial g)^{-1} (I+∂g)−1 就是 prox \text{prox} prox 算子,所以这个不动点迭代就等价于近似点梯度方法。
例子 4(KKT) :对于优化问题
min f 0 ( x ) s.t. g ( x ) ≤ 0 h ( x ) = 0 \begin{aligned} \min\quad& f_0(x) \\ \text{s.t.}\quad& g(x)\le0 \\ & h(x)=0 \end{aligned} mins.t.f0(x)g(x)≤0h(x)=0
拉格朗日函数为 L ( x , λ , ν ) = f 0 ( x ) + λ T g ( x ) + ν T h ( x ) , λ ≥ 0 L(x,\lambda,\nu)=f_0(x)+\lambda^T g(x)+\nu^T h(x),\lambda\ge0 L(x,λ,ν)=f0(x)+λTg(x)+νTh(x),λ≥0,KKT 条件就是要求解方程
T ( x , λ , ν ) = [ ∂ x L ( x , λ , ν ) − f ( x ) + ∂ δ { λ ≥ 0 } ( x ) h ( x ) ] = 0 T(x,\lambda,\nu)=\left[\begin{array}{c} \partial_x L(x,\lambda,\nu) \\ -f(x)+\partial \delta_{\{\lambda\ge0\}}(x) \\ h(x) \end{array}\right]=0 T(x,λ,ν)=⎣⎡∂xL(x,λ,ν)−f(x)+∂δ{λ≥0}(x)h(x)⎦⎤=0
也就是要找到 T ~ = I + T \tilde{T}=I+T T~=I+T 的不动点。
上面几个例子主要为了说明很多优化算法都可以写成不动点迭代的形式,那么要想分析他们的收敛性,只需要分析不动点迭代的收敛性就可以了,下面要讲的就是这件事情。
2. 收敛性分析
要想分析收敛速度,必须要引入的一个性质就是 Lipschitz 连续。
定义:算子 T T T 是 L L L-Lipschitz 的, L ∈ [ 0 , + ∞ ) L\in[0,+\infty) L∈[0,+∞),如果它满足
∥ T x − T y ∥ ≤ L ∥ x − y ∥ , ∀ x , y ∈ H \|T x-T y\| \leq L\|x-y\|, \quad \forall x, y \in \mathcal{H} ∥Tx−Ty∥≤L∥x−y∥,∀x,y∈H
定义:算子 T T T 是 L L L-quasi-Lipschitz 的, L ∈ [ 0 , + ∞ ) L\in[0,+\infty) L∈[0,+∞),如果对任意 x ⋆ ∈ Fix T x^\star\in \text{Fix}T x⋆∈FixT 它满足
∥ T x − x ⋆ ∥ ≤ L ∥ x − x ⋆ ∥ , ∀ x ∈ H \|T x-x^\star\| \leq L\|x-x^\star\|, \quad \forall x \in \mathcal{H} ∥Tx−x⋆∥≤L∥x−x⋆∥,∀x∈H
2.1 收缩算子收敛性
定义:算子 T T T 是收缩算子(contractive),如果它满足 L L L-Lipschitz, L ∈ [ 0 , 1 ) L\in[0,1) L∈[0,1)
定义:算子 T T T 是准收缩算子(quasi-contractive),如果它满足 L L L-quasi-Lipschitz, L ∈ [ 0 , 1 ) L\in[0,1) L∈[0,1)
准收缩算子很形象,它说明每次迭代之后,我们都会距离不动点 x ⋆ x^\star x⋆ 更近一点。
下面是一个证明收敛性的重要定理!
定理(Banach fixed-point theorem):如果 T T T 是收缩算子,那么
- T T T 有唯一的不动点 x ⋆ x^\star x⋆(存在且唯一)
- x k → x ⋆ x^k\to x^\star xk→x⋆(强收敛)
- ∥ x k − x ⋆ ∥ ≤ L k ∥ x 0 − x ⋆ ∥ \| x^k-x^\star\|\le L^k\|x^0-x^\star\| ∥xk−x⋆∥≤Lk∥x0−x⋆∥(线性收敛速度)
证明:略。
例子 1(GD) :对于一般的 min f ( x ) \min f(x) minf(x),我们假设 f f f 为 Lipschitz-differentiable 并且是 strongly-convex 的(回忆GD的收敛速度证明)那么就有(假设 f ∈ C 2 f\in C^2 f∈C2)
m I ≤ ∇ 2 f ≤ L I mI\le \nabla^2 f\le LI mI≤∇2f≤LI
梯度下降的算子为 T = I − γ ∇ f T=I-\gamma \nabla f T=I−γ∇f,我们需要计算这个算子的 Lipschitz 常数
( 1 − α L ) I ≤ D ( I − α ∇ f ) = I − α ∇ 2 f ( x ) ≤ ( I − α m ) I ∥ D ( I − α ∇ f ) ∥ ≤ max ( ∣ 1 − α m ∣ , ∣ 1 − α L ∣ ) \begin{array}{c} (1-\alpha L)I\le D(I-\alpha\nabla f)=I-\alpha \nabla^2 f(x)\le(I-\alpha m)I \\ \| D(I-\alpha\nabla f)\| \le \max(|1-\alpha m|,|1-\alpha L|) \end{array} (1−αL)I≤D(I−α∇f)=I−α∇2f(x)≤(I−αm)I∥D(I−α∇f)∥≤max(∣1−αm∣,∣1−αL∣)
注: T = I − γ ∇ f T=I-\gamma \nabla f T=I−γ∇f 里面的 I I I 表示算子, I − α ∇ 2 f ( x ) I-\alpha \nabla^2 f(x) I−α∇2f(x) 里边的 I I I 就表示对角元素等于 1 的矩阵,虽然形式一样,但意义不太一样。
如果要想 T T T 是收缩算子,则需要 α ∈ ( 0 , 2 / L ) \alpha\in(0,2/L) α∈(0,2/L),这也是为什么我们前面章节证明 GD 收敛性的时候需要步长 t ≤ 2 / L t\le 2/L t≤2/L。
例子 2:如果是对于一般的算子,我们想要求解 0 ∈ F ( x ) 0\in F(x) 0∈F(x),类比梯度下降方法,可以有 x k + 1 = x k − α F x k x^{k+1}=x^k-\alpha Fx^k xk+1=xk−αFxk, T = I − α F T=I-\alpha F T=I−αF。类似的,我们也假设 F F F 为 m m m strongly monotone, L L L-Lipschitz 的,那么有
∥ T x − T y ∥ 2 2 = ∥ ( I − α F ) ( x ) − ( I − α F ) ( y ) ∥ 2 2 = ∥ x − y ∥ 2 2 − 2 α ( F x − F y ) T ( x − y ) + α 2 ∥ F x − F y ∥ 2 2 ≤ ( 1 − 2 α m + α 2 L 2 ) ∥ x − y ∥ 2 \begin{aligned} \| Tx-Ty\|^2_2 &=\| (I-\alpha F)(x)-(I-\alpha F)(y)\|^2_2 \\ &= \|x-y\|_2^2 - 2\alpha(Fx-Fy)^T(x-y)+\alpha^2\|Fx-Fy\|^2_2 \\ &\le (1-2\alpha m+\alpha^2L^2)\|x-y\|^2 \end{aligned} ∥Tx−Ty∥22=∥(I−αF)(x)−(I−αF)(y)∥22=∥x−y∥22−2α(Fx−Fy)T(x−y)+α2∥Fx−Fy∥22≤(1−2αm+α2L2)∥x−y∥2
所以当 α ∈ ( 0 , 2 m L 2 ) \alpha\in\left(0,\frac{2m}{L^2}\right) α∈(0,L22m) 的时候 T T T 是收缩算子,可以证明收敛性。
跟前面梯度下降对比,前面只要求 α < 2 / L \alpha <2/L α<2/L,所以梯度下降的要求更宽松。即使不满足强凸性质,梯度下降也能保证收敛,但是这里就必须要有 m m m strongly monotone,这是因为梯度算子提供了更多的信息。
2.2 非扩张算子收敛性
前面的收缩算子要求 L < 1 L<1 L<1,这个条件还是比较强的,很多时候只能得到 L = 1 L=1 L=1,这个时候被称为 nonexpansive,也就是非扩张的。这个时候
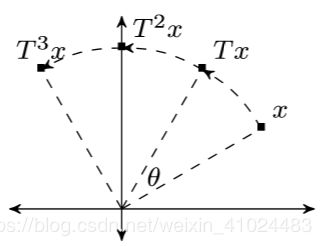
- T T T 可能不存在不动点 x ⋆ x^\star x⋆
- 如果 x ⋆ x^\star x⋆ 存在,不动点迭代 x k + 1 = T x k x^{k+1}=Tx^k xk+1=Txk 有界
- 可能会发散(这个发散我个人不太理解,或许不收敛也被认为是发散)
比如说旋转、反射操作,如图所示
那么对于这种算子怎么证明收敛性呢?如果得不到收缩性质,那么我们可以放松一点要求,比如得到下面的
∥ T x − T y ∥ 2 ≤ ∥ x − y ∥ 2 − η ∥ R x − R y ∥ 2 , ∀ x , y ∈ H \|T x-T y\|^{2} \leq\|x-y\|^{2}-\eta\|R x-R y\|^{2}, \quad \forall x, y \in \mathcal{H} ∥Tx−Ty∥2≤∥x−y∥2−η∥Rx−Ry∥2,∀x,y∈H
这个算子 R R R 一会再说,虽然我们还是只能有 L = 1 L=1 L=1,但是每次迭代之后都可以减少一点小尾巴,累积起来就能收敛到不动点了。那么就让我们再引入一些定义吧。
定义不动点残差算子 R : = I − T R:=I-T R:=I−T,有 R x ⋆ = 0 ⟺ x ⋆ = T x ⋆ Rx^\star=0\iff x^\star=Tx^\star Rx⋆=0⟺x⋆=Tx⋆。
定义:若 T T T 对于某些 η > 0 \eta>0 η>0 满足下式,则称其为平均算子(averaged operator)
∥ T x − T y ∥ 2 ≤ ∥ x − y ∥ 2 − η ∥ R x − R y ∥ 2 , ∀ x , y ∈ H \|T x-T y\|^{2} \leq\|x-y\|^{2}-\eta\|R x-R y\|^{2}, \quad \forall x, y \in \mathcal{H} ∥Tx−Ty∥2≤∥x−y∥2−η∥Rx−Ry∥2,∀x,y∈H
定义:若 T T T 对于某些 η > 0 \eta>0 η>0 满足下式,则称其为准平均算子(quasi-averaged operator)
∥ T x − x ∗ ∥ 2 ≤ ∥ x − x ∗ ∥ 2 − η ∥ R x ∥ 2 , ∀ x ∈ H \left\|T x-x^{*}\right\|^{2} \leq\left\|x-x^{*}\right\|^{2}-\eta\|R x\|^{2}, \quad \forall x \in \mathcal{H} ∥Tx−x∗∥2≤∥x−x∗∥2−η∥Rx∥2,∀x∈H
我们也可以表示为 η : = 1 − α α \eta:=\frac{1-\alpha}{\alpha} η:=α1−α,从而将上面平均算子称为 α \alpha α-averaged operator。如果 α = 1 / 2 \alpha=1/2 α=1/2,称 T T T 为 firmly nonexpansive;如果 α = 1 \alpha=1 α=1,称 T T T 为 nonexpansive。
引理: T T T 是 α \alpha α-averaged operator,当且仅当存在一个 nonexpansive T ′ T' T′ 使得
T = ( 1 − α ) I + α T ′ T=(1-\alpha)I+\alpha T' T=(1−α)I+αT′
或者等价的有算子
T ′ : = ( ( 1 − 1 α ) I + 1 α T ) T^{\prime}:=\left(\left(1-\frac{1}{\alpha}\right) I+\frac{1}{\alpha} T\right) T′:=((1−α1)I+α1T)
是 nonexpansive。
证明:通过代数运算可以得到
α ( ∥ x − y ∥ 2 − ∥ T ′ x − T ′ y ∥ 2 ) = ∥ x − y ∥ 2 − ∥ T x − T y ∥ 2 − 1 − α α ∥ R x − R y ∥ 2 \alpha\left(\|x-y\|^{2}-\left\|T^{\prime} x-T^{\prime} y\right\|^{2}\right)=\|x-y\|^{2}-\|T x-T y\|^{2}-\frac{1-\alpha}{\alpha}\|R x-R y\|^{2} α(∥x−y∥2−∥T′x−T′y∥2)=∥x−y∥2−∥Tx−Ty∥2−α1−α∥Rx−Ry∥2
因此 T ′ T' T′ nonexpansive ⟺ \iff ⟺ T α \alpha α-averaged。证毕。
有了 α \alpha α-averaged 性质,我们也可以得到一个收敛性的定理。
定理(Krasnosel’skii): T T T 为 α \alpha α-averaged 算子,且不动点存在,则迭代方法
x k + 1 ← T x k x^{k+1}\leftarrow Tx^k xk+1←Txk
弱收敛至 T T T 的不动点。证明:略。
定理(Mann’s version): T T T 为 nonexpansive 算子,且不动点存在,则迭代方法
x k + 1 ← ( 1 − λ k ) x k + λ k T x k x^{k+1} \leftarrow\left(1-\lambda_{k}\right) x^{k}+\lambda_{k} T x^{k} xk+1←(1−λk)xk+λkTxk
弱收敛至 T T T 的不动点,只要满足
λ k > 0 , ∑ k λ k ( 1 − λ k ) = ∞ \lambda_{k}>0, \quad \sum_{k} \lambda_{k}\left(1-\lambda_{k}\right)=\infty λk>0,k∑λk(1−λk)=∞
证明:略。
Mann’s version 相当于是对 Krasnosel’skii 的一个推广,每一步都取一个不同的 α \alpha α。
例子 1(PPA) :对于 min f ( x ) \min f(x) minf(x),近似点算子
T : = prox λ f T:=\operatorname{prox}_{\lambda f} T:=proxλf
就是 firmly-nonexpansive,因此可以弱收敛。
2.3 复合算子
对于多个算子复合,有以下性质:
- T 1 , … , T m : H → H T_{1}, \ldots, T_{m}: \mathcal{H} \rightarrow \mathcal{H} T1,…,Tm:H→H contractive ⟹ T 1 ∘ ⋯ ∘ T m \Longrightarrow T_{1} \circ \cdots \circ T_{m} ⟹T1∘⋯∘Tm contractive
- T 1 , … , T m : H → H T_{1}, \ldots, T_{m}: \mathcal{H} \rightarrow \mathcal{H} T1,…,Tm:H→H nonexpansive ⟹ T 1 ∘ ⋯ ∘ T m \Longrightarrow T_{1} \circ \cdots \circ T_{m} ⟹T1∘⋯∘Tm nonexpansive
- T 1 , … , T m : H → H T_{1}, \ldots, T_{m}: \mathcal{H} \rightarrow \mathcal{H} T1,…,Tm:H→H averaged ⟹ T 1 ∘ ⋯ ∘ T m \Longrightarrow T_{1} \circ \cdots \circ T_{m} ⟹T1∘⋯∘Tm averaged
- T i T_i Ti 是 α i \alpha_i αi-averaged(允许 α i = 1 \alpha_i=1 αi=1) ⟹ T 1 ∘ ⋯ ∘ T m \Longrightarrow T_{1} \circ \cdots \circ T_{m} ⟹T1∘⋯∘Tm 是 α \alpha α-averaged,其中
α = m m − 1 + 1 max i α i \alpha=\frac{m}{m-1+\frac{1}{\max _{i} \alpha_{i}}} α=m−1+maxiαi1m
例子:如第一小节的投影梯度、PG。
3. 更一般的情况
我们的优化问题可以概括为求解方程
0 ∈ ( A + B ) ( x ) 0\in(A+B)(x) 0∈(A+B)(x)
其中 A , B A,B A,B 为算子,那么对这个式子做变形就能得到很多方法。
Forward-backward:
0 ∈ ( A + B ) ( x ) ⟺ 0 ∈ ( I + α B ) ( x ) − ( I − α A ) ( x ) ⟺ ( I − α A ) ( x ) ∈ ( I + α B ) ( x ) ⟺ x = ( I + α B ) − 1 ( I − α A ) ( x ) \begin{aligned} 0\in(A+B)(x) &\iff 0\in(I+\alpha B)(x)-(I-\alpha A)(x) \\ &\iff (I-\alpha A)(x)\in(I+\alpha B)(x) \\ &\iff x=(I+\alpha B)^{-1}(I-\alpha A)(x) \end{aligned} 0∈(A+B)(x)⟺0∈(I+αB)(x)−(I−αA)(x)⟺(I−αA)(x)∈(I+αB)(x)⟺x=(I+αB)−1(I−αA)(x)
Forward-backward-forward:
0 ∈ ( A + B ) ( x ) ⟺ x = ( I + α B ) − 1 ( I − α A ) ( x ) ⟺ ( I − α A ) ( x ) = ( I − α A ) ( I + α B ) − 1 ( I − α A ) ( x ) ⟺ x = ( ( I − α A ) ( I + α B ) − 1 ( I − α A ) + α A ) ( x ) \begin{aligned} 0\in(A+B)(x) &\iff x=(I+\alpha B)^{-1}(I-\alpha A)(x) \\ &\iff (I-\alpha A)(x)= (I-\alpha A)(I+\alpha B)^{-1}(I-\alpha A)(x) \\ &\iff x=\left((I-\alpha A)(I+\alpha B)^{-1}(I-\alpha A)+\alpha A\right)(x) \end{aligned} 0∈(A+B)(x)⟺x=(I+αB)−1(I−αA)(x)⟺(I−αA)(x)=(I−αA)(I+αB)−1(I−αA)(x)⟺x=((I−αA)(I+αB)−1(I−αA)+αA)(x)
Combetts-Pesquest:
0 ∈ ( A + B + C ) ( x ) ⟺ { 0 ∈ A x + u + C x u ∈ B x ⟺ 0 ∈ [ A x B − 1 u ] + [ u + C x − x ] \begin{aligned} 0\in(A+B+C)(x) &\iff \begin{cases}0\in Ax+u+Cx \\ u\in Bx \end{cases} \\ &\iff 0\in \left[\begin{array}{c}Ax \\ B^{-1}u\end{array}\right] + \left[\begin{array}{c}u+Cx \\ -x\end{array}\right] \end{aligned} 0∈(A+B+C)(x)⟺{0∈Ax+u+Cxu∈Bx⟺0∈[AxB−1u]+[u+Cx−x]
DR splitting:
0 ∈ ( A + B ) ( x ) ⟺ ( 1 2 I + 1 2 C A R B ) ( z ) = z , x = R B ( z ) \begin{aligned} 0\in(A+B)(x) \iff (\frac{1}{2}I+\frac{1}{2}C_A R_B)(z)=z,\quad x=R_B(z)\\ \end{aligned} 0∈(A+B)(x)⟺(21I+21CARB)(z)=z,x=RB(z)
其中
C A C_A CA:Cayley operator, C A = 2 R A − I = 2 prox f − I C_A=2R_A-I=2\text{prox}_f-I CA=2RA−I=2proxf−I
R B R_B RB:resolvent operator, R B = ( z ) = ( I + B ) − 1 ( z ) R_B=(z)=(I+B)^{-1}(z) RB=(z)=(I+B)−1(z)
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
最优化方法 15:梯度方法
最优化方法 16:次梯度
最优化方法 17:次梯度下降法
最优化方法 18:近似点算子 Proximal Mapping
最优化方法 19:近似梯度下降
最优化方法 20:对偶近似点梯度下降法
最优化方法 21:加速近似梯度下降方法
最优化方法 22:近似点算法 PPA
最优化方法 23:算子分裂法 & ADMM
最优化方法 24:ADMM
最优化方法 25:PDHG
最优化方法 26:不动点迭代