3.6栈与递归(上)
3.6栈与递归(上)
栈非常重要的一个应用就是在程序设计语言中用来实现递归。
递归是指在定 义自身的同时又出现了对自身的引用。
- 如果一个函数在其定义体内直接调用自 己,则称为直接递归函数;
- 如果一个函数经过一系列的中间调用语句,通过其他函数间接调用自己,则称为间接递归函数。
具有递归特性的问题
1、递归定义的数学函数

上述 Ackerman 函数可用一个简单的 C 语言函数描述如下:
int ack(int m,int n)
{
if(m==0)
return n+1;
else if (n==0)
return ack(m-1,1);
else
return ack(m-1, ack(m,n-1));
}
2、递归数据结构的处理
在后续章节将要学习的一些数据结构,如广义表、二叉树、树等结构其本身 均具有固有的递归特性,因此可以自然地采用递归法进行处理。
3、递归求解方法
许多问题的求解过程可以用递归分解的方法描述,一个典型的例子是著名的 汉诺塔问题(Hanoi)问题。
n 阶 Hanoi 塔问题:假设有三个分别命名为X,Y 和 Z 的塔座,在塔座 X 上插 有 n 个直径大小各不相同、从小到大编号为 1,2,… ,n 的圆盘。现要求将塔 座 X 上的 n 个圆盘移至塔座 Z 上,并仍按同样顺序叠排。
圆盘移动时必须遵循下列规则:
① 每次只能移动一个圆盘;
② 圆盘可以插在 X,Y 和 Z 中的任何一个塔座上;
③ 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。
【算法思想】
当 n=1 时,问题比较简单,只要将编号为 1 的圆盘从座 X 直接移动到塔座 Z 上即可;
当 n>1 时,需利用塔座 Y 作辅助塔座,若能设法将压在编号为 n 的圆盘上的 n-1 个圆盘从塔座 X(依照上述原则)移至塔座 Y 上,则可先将编为 n 的圆盘从塔座 X 移至塔座 Z 上,然后再将塔座 Y 上的 n-1 个圆盘(依照上述原则)移至塔座 Z 上。
而如何将 n-1 个圆盘从一个塔座移至另一个塔座问题是一个和原问题具有相同特征属性的问题,只是问题的规模小于 1,因此可以用同样方法求解。由此可得如下求解 n 阶 Hanoi 塔问题的递归算法。
【算法描述】
void hanoi(int n, char x, char y, char z) /* 将塔座 X 上从上到下编号为 1 至 n,且按直径由小到大叠放的 n 个圆盘,按 规则搬到塔座 Z 上,Y 用作辅助塔座。*/
{
if(n==1)
move(x,1,z); /*将编号为 1 的圆盘从 x 移动 z*/
else
{
hanoi(n-1,x,z,y); /* 将X 上编号为 1至 n-1的圆盘移到y,z 作辅助 塔 */
move(x,n,z); /* 将编号为 n 的圆盘从 x 移到 z */
hanoi(n-1, y,x ,z); /* 将 y 上编号为 1 至 n-1 的圆盘移到 z,x 作辅 助塔 */
}
}
下面给出三个盘子搬动时 hanoi(3, A, B , C) 的递归调用过程:

递归方法的优点
通过上面的例子可看出,递归既是强有力的数学方法,也是程序设计中一个 很有用的工具。其特点是对问题描述简洁,结构清晰,程序的正确性容易证明。
设计递归算法的方法
递归算法就是在算法中直接或间接调用算法本身的算法。
使用递归算法的前提有两个:
⑴原问题可以层层分解为类似的的子问题,且子问题比原问题的规模更小。
⑵规模最小的子问题具有直接解。
设计递归算法的原则是用自身的简单情况来定义自身,设计递归算法的方法 是:
⑴寻找分解方法:将原问题转化为子问题求解。( 例:n!=n*(n-1)! )
⑵设计递归出口:即根据规模最小的子问题,确定递归终止条件。(例:求 解 n!时,当 n=1 时,n!=1)。
递归过程的实现
递归进层(i→i +1 层)系统需要做三件事:
- ⑴ 保留本层参数与返回地址;
- ⑵ 为被调用函数的局部变量分配存储区,给下层参数赋值;
- ⑶ 将程序转移到被调函数的入口。
而从被调用函数返回调用函数之前,递归退层(i←i +1 层)系统也应完成 三件工作:
- ⑴ 保存被调函数的计算结果;
- ⑵ 释放被调函数的数据区,恢复上层参数;
- ⑶ 依照被调函数保存的返回地址,将控制转移回调用函数。
当递归函数调用时,应按照“后调用先返回”的原则处理调用过程,因此上 述函数之间的信息传递和控制转移必须通过栈来实现。
系统将整个程序运行时所需的数据空间安排在一个栈中,每当调用一个函数时,就为它在栈顶分配一个存储区,而每当从一个函数退出时,就释放它的存储区。显然,当前正在运行的函数的数据区必在栈顶。
一个递归函数的运行过程调用函数和被调用函数是同一个函数,因此,与每 次调用时相关的一个重要的概念是递归函数运行的“层次”。
假设调用该递归函数的主函数为第 0 层,则从主函数调用递归函数为进入第 1 层;
从第 i 层递归调用本函数为进入“下一层”,即第 i+1 层。
反之,退出第 i 层递归应返回至“上 一层”,即第 i-1 层。
为了保证递归函数正确执行,系统需设立一个递归工作栈作为整个递归函数运行期间使用的数据存储区。每层递归所需信息构成一个工作记录,其中包括所有的实在参数、所有的局部变量以及上一层的返回地址。
每进入一层递归,就产生一个新的工作记录压入栈顶。
每退出一层递归,就从栈顶弹出一个工作记录。
因此当前执行层的工作记录必为递归工作栈栈顶的工作记录, 称这个记录为活动记录,并称指示活动记录的栈顶指针为当前环境指针。
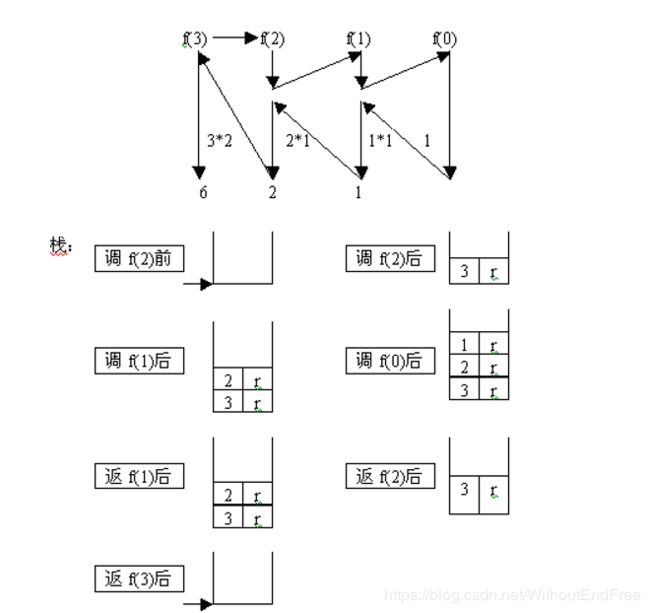
int f(int n ) /* 设 n>=0 */
{
if (n==0)
return (1);
else
return (n*f(n-1)); }
- 保存本层参数、返回地址
- 分配局部数据空间,传递参数
- 转第一条指令
递归退层 3 件事:
- 恢复上层
- 传递结果
- 转断点执行
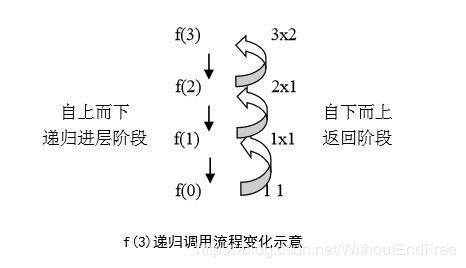
可以看出,整个计算包括两个阶段:
自上而下递归调用(进层),自下而上 返回结果(退层)。
计算结果在第二阶段,先计算 f(0) f(1) …f(n),所有递归调用直接或间接依赖 f(0)。