凸优化学习-(十三)拟凸函数与拟凸问题
凸优化学习
今天学习拟凸函数与拟凸问题。
学习笔记
一、 α -sublevel-set \alpha\text{-sublevel-set} α-sublevel-set
定义:
若 f : R n → R , 其 α -sublevel-set 为 S α = { x ∈ dom f ∣ f ( x ) ≤ α } 若f:R^n\rightarrow R,其\alpha\text{-sublevel-set}为S_\alpha=\lbrace x\in\text{dom}f\mid f(x)\le \alpha\rbrace 若f:Rn→R,其α-sublevel-set为Sα={x∈domf∣f(x)≤α}
凸函数所有的 α -sublevel-set \alpha\text{-sublevel-set} α-sublevel-set都是凸集。
若函数的 α -sublevel-set \alpha\text{-sublevel-set} α-sublevel-set都是凸集,该函数不一定为凸函数。

α -sublevel-set \alpha\text{-sublevel-set} α-sublevel-set就是画一条横线,这条横线和它下方的函数构成的区域。
二、拟凸函数 Quasi Convex Function \text{Quasi Convex Function} Quasi Convex Function
1.定义
定义1:
Quasi Convex : 对 ∀ α , S α = { x ∈ dom f ∣ f ( x ) ≤ α } 为 凸 。 \text{Quasi Convex}:对\forall\alpha,S_\alpha=\lbrace x\in\text{dom}f\mid f(x)\le \alpha\rbrace为凸。 Quasi Convex:对∀α,Sα={x∈domf∣f(x)≤α}为凸。
即拟凸函数的所有的 α -sublevel-set \alpha\text{-sublevel-set} α-sublevel-set都是凸集。
定义2:
max { f ( x ) , f ( y ) } ≥ f ( θ x + ( 1 − θ ) y ) dom f 为 凸 , ∀ x , y ∈ dom f , 0 ≤ θ ≤ 1 \max\lbrace f(x),f(y)\rbrace\ge f\big(\theta x+(1-\theta)y\big)\\ \text{dom}f为凸,\forall x,y\in\text{dom}f,0\le\theta\le1 max{f(x),f(y)}≥f(θx+(1−θ)y)domf为凸,∀x,y∈domf,0≤θ≤1
一般的拟凸函数:

拟凸函数也称 unimodel function \text{unimodel function} unimodel function单模态函数。

一些类似定义:
Quasi Concave : 对 ∀ α , S α = { x ∈ dom f ∣ f ( x ) ≥ α } 为 凸 。 \text{Quasi Concave}:对\forall\alpha,S_\alpha=\lbrace x\in\text{dom}f\mid f(x)\ge \alpha\rbrace为凸。 Quasi Concave:对∀α,Sα={x∈domf∣f(x)≥α}为凸。
Quasi Linear : 对 ∀ α , S α = { x ∈ dom f ∣ f ( x ) = α } 为 凸 。 \text{Quasi Linear}:对\forall\alpha,S_\alpha=\lbrace x\in\text{dom}f\mid f(x)= \alpha\rbrace为凸。 Quasi Linear:对∀α,Sα={x∈domf∣f(x)=α}为凸。
例1:向量的长度
形如:
f ( x ) = { max { i , x ⃗ i ≠ 0 } x ≠ 0 0 x = 0 f(x)=\begin{cases} \max\lbrace i,\vec x_i\ne0\rbrace &x\ne0\\ 0& x=0 \end{cases} f(x)={max{i,xi=0}0x=0x=0
即是 x ⃗ \vec x x中最后一个非零元素的位置。
因为对所有的 f ( x ) ≤ α f(x)\le \alpha f(x)≤α都是凸集。
例2:线性分数函数
形如:
f ( x ) = a T x + b c T x + d dom f = { x ∣ c T x − d > 0 } f(x)=\frac{a^Tx+b}{c^Tx+d}\qquad \text{dom}f=\lbrace x\mid c^Tx-d>0\rbrace f(x)=cTx+daTx+bdomf={x∣cTx−d>0}
2、拟凸函数与凸函数对比
1.定义
凸函数:
R n → R 为 凸 , 则 dom f 为 凸 , ∀ x , y ∈ dom f , 0 ≤ θ ≤ 1 有 θ f ( x ) + ( 1 − θ ) f ( y ) ≥ f ( θ x + ( 1 − θ ) y ) R^n\rightarrow R为凸,则\text{dom}f为凸,\forall x,y\in\text{dom}f,0\le\theta\le1有\\ \theta f(x)+(1-\theta)f(y)\ge f\big(\theta x+(1-\theta)y\big) Rn→R为凸,则domf为凸,∀x,y∈domf,0≤θ≤1有θf(x)+(1−θ)f(y)≥f(θx+(1−θ)y)
拟凸函数:
R n → R 为 拟 凸 , 则 dom f 为 凸 , ∀ x , y ∈ dom f , 0 ≤ θ ≤ 1 有 max { f ( x ) , f ( y ) } ≥ f ( θ x + ( 1 − θ ) y ) R^n\rightarrow R为拟凸,则\text{dom}f为凸,\forall x,y\in\text{dom}f,0\le\theta\le1有\\ \max\lbrace f(x),f(y)\rbrace\ge f\big(\theta x+(1-\theta)y\big) Rn→R为拟凸,则domf为凸,∀x,y∈domf,0≤θ≤1有max{f(x),f(y)}≥f(θx+(1−θ)y)
几何对比
凸函数:

由定义可得,就是任意 x x x和 y y y的连线都要高于它们之间的函数图像。
拟凸函数:

由定义可得,就是任意 x x x和 y y y,高的那一个在 x x x和 y y y之间的线段要高于它们之间的函数图像。
2.拟凸函数和凸函数梯度下降对比:

拟凸函数在进行梯度下降时,没有凸函数那么“顺滑”,有可能会下降到函数的另一半,但是只要梯度下降算法得当,拟凸函数还是有很好的性质。
3.深入理解拟凸函数。
①可微拟凸函数一阶条件
凸函数:
dom f 为 凸 , f ( y ) ≥ f ( x ) + ∇ T f ( x ) ( y − x ) ∀ x , y ∈ dom f \text{dom}f为凸,f(y)\ge f(x)+\nabla^Tf(x)(y-x)\ \ \forall x,y\in\text{dom}f domf为凸,f(y)≥f(x)+∇Tf(x)(y−x) ∀x,y∈domf
拟凸函数:
dom f 为 凸 , f ( y ) ≤ f ( x ) ⇒ ∇ T f ( x ) ( y − x ) ≤ 0 ∀ x , y ∈ dom f \text{dom}f为凸,f(y)\le f(x)\Rightarrow\nabla^Tf(x)(y-x)\le0\ \ \forall x,y\in\text{dom}f domf为凸,f(y)≤f(x)⇒∇Tf(x)(y−x)≤0 ∀x,y∈domf
证明 dom f 为 凸 , f ( y ) ≤ f ( x ) ⇒ ∇ T f ( x ) ( y − x ) ≤ 0 ∀ x , y ∈ dom f \text{dom}f为凸,f(y)\le f(x)\Rightarrow\nabla^Tf(x)(y-x)\le0\ \ \forall x,y\in\text{dom}f domf为凸,f(y)≤f(x)⇒∇Tf(x)(y−x)≤0 ∀x,y∈domf:
由 f 拟 凸 得 : max { f ( x ) , f ( y ) } ≥ f ( θ x + ( 1 − θ ) y ) 0 ≤ θ ≤ 1 设 f ( y ) ≤ f ( x ) , 上 式 即 为 : f ( x ) ≥ f ( θ x + ( 1 − θ ) y ) ⇒ f ( θ x + ( 1 − θ ) y ) − f ( x ) ≤ 0 ⇔ f ( θ x + ( 1 − θ ) y ) − f ( θ x + ( 1 − θ ) x ) ≤ 0 ⇔ f ( θ x + ( 1 − θ ) y ) − f ( θ x + ( 1 − θ ) x ) ( 1 − θ ) ( y − x ) ( 1 − θ ) ( y − x ) ≤ 0 ⇔ θ → 1 f ′ ( x ) ( y − x ) ≤ 0 即 证 f ( y ) ≤ f ( x ) ⇒ ∇ T f ( x ) ( y − x ) ≤ 0 ∀ x , y ∈ dom f 由f拟凸得:\max\lbrace f(x),f(y)\rbrace\ge f\big(\theta x+(1-\theta)y\big)\quad 0\le\theta \le1\\ \begin{aligned} 设f(y)\le f(x),上式即为:& f(x)\ge f\big(\theta x+(1-\theta)y\big)\\ \Rightarrow&f\big(\theta x+(1-\theta)y\big)-f(x)\le0\\ \Leftrightarrow&f\big(\theta x+(1-\theta)y\big)-f\big(\theta x+(1-\theta)x\big)\le0\\ \Leftrightarrow&\frac{f\big(\theta x+(1-\theta)y\big)-f\big(\theta x+(1-\theta)x\big)}{(1-\theta)(y-x)}(1-\theta)(y-x)\le0\\ \stackrel{\theta\rightarrow1}\Leftrightarrow&f'(x)(y-x)\le0\\ \end{aligned}\\ 即证f(y)\le f(x)\Rightarrow\nabla^Tf(x)(y-x)\le0\ \ \forall x,y\in\text{dom}f 由f拟凸得:max{f(x),f(y)}≥f(θx+(1−θ)y)0≤θ≤1设f(y)≤f(x),上式即为:⇒⇔⇔⇔θ→1f(x)≥f(θx+(1−θ)y)f(θx+(1−θ)y)−f(x)≤0f(θx+(1−θ)y)−f(θx+(1−θ)x)≤0(1−θ)(y−x)f(θx+(1−θ)y)−f(θx+(1−θ)x)(1−θ)(y−x)≤0f′(x)(y−x)≤0即证f(y)≤f(x)⇒∇Tf(x)(y−x)≤0 ∀x,y∈domf
证明 f f f拟凸,当 ∀ x , y ∈ dom f f ( y ) ≤ f ( x ) , ∇ T f ( x ) ( y − x ) ≤ 0 : \forall x,y\in\text{dom}f\quad f(y)\le f(x),\nabla^Tf(x)(y-x)\le0: ∀x,y∈domff(y)≤f(x),∇Tf(x)(y−x)≤0:
即 证 max { f ( x ) , f ( y ) } − f ( θ x + ( 1 − θ ) y ) ≥ 0 0 ≤ θ ≤ 1 ⇔ f ( x ) − f ( θ x + ( 1 − θ ) y ) ≥ 0 = f ( θ x + ( 1 − θ ) x ) − f ( θ x + ( 1 − θ ) y ) ( 1 − θ ) ( x − y ) ( 1 − θ ) ( x − y ) ≤ 0 = θ → 1 f ′ ( x ) ( x − y ) ≥ 0 由 ∇ T f ( x ) ( y − x ) ≤ 0 显 然 成 立 。 \begin{aligned} 即证&\max\lbrace f(x),f(y)\rbrace- f\big(\theta x+(1-\theta)y\big)\ge0\quad 0\le\theta \le1\\ \Leftrightarrow&f(x)- f\big(\theta x+(1-\theta)y\big)\ge0\\ =&\frac{f\big(\theta x+(1-\theta)x\big)-f\big(\theta x+(1-\theta)y\big)}{(1-\theta)(x-y)}(1-\theta)(x-y)\le0\\ \stackrel{\theta\rightarrow1}=&f'(x)(x-y)\ge0\\ &由\nabla^Tf(x)(y-x)\le0显然成立。 \end{aligned} 即证⇔==θ→1max{f(x),f(y)}−f(θx+(1−θ)y)≥00≤θ≤1f(x)−f(θx+(1−θ)y)≥0(1−θ)(x−y)f(θx+(1−θ)x)−f(θx+(1−θ)y)(1−θ)(x−y)≤0f′(x)(x−y)≥0由∇Tf(x)(y−x)≤0显然成立。
由一阶条件得出的推论:
凸函数:若 ∇ f T ( x ) = 0 \nabla f^T(x)=0 ∇fT(x)=0,则 ∀ y f ( y ) ≥ f ( x ) \forall y\quad f(y)\ge f(x) ∀yf(y)≥f(x)
拟凸函数:若 ∇ f T ( x ) = 0 f ( y ) ≤ f ( x ) \nabla f^T(x)=0\ f(y)\le f(x) ∇fT(x)=0 f(y)≤f(x),则 ∀ y 0 ≤ 0 \forall y\quad 0\le0 ∀y0≤0
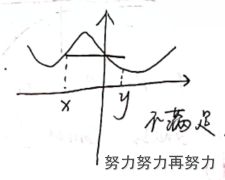
即拟凸函数一阶偏导为零无意义。
如图中三个一阶偏导为零的点。
②可微拟凸函数二阶条件(前提:二阶可微)
凸函数: dom f \text{dom}f domf为凸,且 ∇ 2 f ( x ) ≥ 0 ∀ x ∈ dom f \nabla^2f(x)\ge0\quad \forall x\in \text{dom}f ∇2f(x)≥0∀x∈domf
拟凸函数: dom f \text{dom}f domf为凸 ⇔ y T ∇ f ( x ) ≥ 0 ⇒ y T ∇ 2 f ( x ) y ≥ 0 \Leftrightarrow y^T\nabla f(x)\ge0\Rightarrow y^T\nabla^2f(x)y\ge0 ⇔yT∇f(x)≥0⇒yT∇2f(x)y≥0
两者对比:凸函数要求所有的点二阶偏导大于等于0,而拟凸函数仅要求在一阶偏导等于0的点其二阶偏导大于零。
例: f ( x ) = x 3 f(x)=x^3 f(x)=x3

三、拟凸问题 Quasi-Convex problem \text{Quasi-Convex problem} Quasi-Convex problem
目标函数为拟凸函数的优化问题。
例1:向量的零范数——将普通问题转化为拟凸问题
形如:
f ( x ) = ∥ x ∥ 0 f(x)=\|x\|_0 f(x)=∥x∥0
其几何图像为:

其对应的y优化问题:
min ∥ x ∥ 0 s.t x ∈ C \begin{aligned} & \min \|x\|_0\\ & \text{s.t}\quad x\in C \end{aligned} min∥x∥0s.tx∈C
进行凸松弛1:
min ∥ x ∥ 1 s.t x ∈ C \begin{aligned} & \min \|x\|_1\\ & \text{s.t}\quad x\in C \end{aligned} min∥x∥1s.tx∈C

松弛太多了(形状差太远)。
进行凸松弛2:
min log ( x T x + 1 ) s.t x ∈ C \begin{aligned} & \min \log(x^Tx+1)\\ & \text{s.t}\quad x\in C \end{aligned} minlog(xTx+1)s.tx∈C

四、对数凸和对数凹 log convex and log concave \text{log convex and log concave} log convex and log concave
形如:
log convex : f : R n → R 为 log convex 当 f ( x ) > 0 , ∀ x ∈ dom f , 且 log f 为 凸 函 数 log concave : f : R n → R 为 log concave 当 f ( x ) > 0 , ∀ x ∈ dom f , 且 log f 为 凹 函 数 \text{log convex}:\quad f:R^n\rightarrow R为\text{log convex}当f(x)>0,\forall x\in \text{dom}f,且\log f为凸函数\\ \text{log concave}:\quad f:R^n\rightarrow R为\text{log concave}当f(x)>0,\forall x\in \text{dom}f,且\log f为凹函数 log convex:f:Rn→R为log convex当f(x)>0,∀x∈domf,且logf为凸函数log concave:f:Rn→R为log concave当f(x)>0,∀x∈domf,且logf为凹函数
若 f f f为凸, log f \log f logf不一定为对数凸,若 log f \log f logf为对数凸, f f f一定为凸;
若 f f f为凹, f > 0 f>0 f>0, log f \log f logf一定为对数凹,若 log f \log f logf为对数凹, f f f不一定为凹;
可以用函数组合性质来判断,也可以想象 log \log log把 f f f掰下去。
个人思考
拟凸函数和拟凸问题有着较好的性质,我们常常把优化问题分为凸问题以及非凸问题,其中凸问题是比较容易的问题,非凸问题是比较难以处理的问题。但非凸问题中的拟凸问题也是属于非凸问题中比较好处理的一类问题,当我们拿到一个非凸问题的时候,对其进行凸松弛,松弛成类似的拟凸问题也不失为一种方法。