MATLAB----2019/8/3
回归分析
- 复共线性与有偏估计方法
(1)岭回归用于处理下面两类问题:
1.数据点少于变量个数
2.变量间存在共线性
(2) 判断变量之间是否有共线性为:
变量间存在共线性是,最小二乘回归得到的系数不稳定,方差很大
x=x0(:,2:4);
y=x0(:,5);
k=0:0.01:0.1;
b1=ridge(y,x,k,0);
%岭回归B = ridge(y,X,k,scaled)命令中:y- 响应数据;X- 预测数据,k- 岭参数,scaled- 缩放标志(0)
yhat=repmat(b1(1,:),[11,1])+x*b1(2:4,:);
Q=(dist(y',yhat)).^2
plot(k,b1(2:4,:)');
legend('x1','x2','x3')
tx=zscore(x0);
%原始数据标准化
m=4;
x1=tx(:,2:m);
y=tx(:,end);
[p,A]=eig(x1'*x1);
lamda=diag(A);
Z=x1*p;
[a,aci,r,rci,st]=regress(y,Z);
%求最小二乘估计和样本方差
k=st(4)/max(a.^2)
%求岭参数的值
b1=ridge(x0(:,end),x0(:,2:end-1),k,0)
%回归方程的参数
- 主成分估计
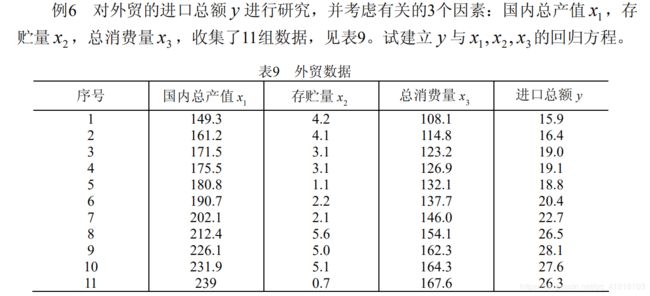
例六解:
x0=[1 149.3 4.2 108.1 15.9
2 161.2 4.1 114.8 16.4
3 171.5 3.1 123.2 19.0
4 175.5 3.1 126.9 19.1
5 180.8 1.1 132.1 18.8
6 190.7 2.2 137.7 20.4
7 202.1 2.1 146.0 22.7
8 212.4 5.6 154.1 26.5
9 226.1 5.0 162.3 28.1
10 231.9 5.1 164.3 27.6
11 239 0.7 167.6 26.3];
x1=x0(:,2:end-1);
y=x0(:,end);
mu=mean(x1);
sig=std(x1);
muy=mean(y);
sigy=std(y);
xz=zscore(x1);
yz=zscore(y);
%数据标准化
[c,s,t]=princomp(xz)
m=2;
%取前两个主成分
a=s(:,1:m)\y
%主成分的回归方程系数
ab=c(:,1:m)*a
%标准化变量的回归方程系数
b=[muy-sigy*(mu./sig)*ab,sigy*ab'./sig]
%原始变量的回归方程的系数
%以回归系数和自变量为输入变量,将要拟合的模型写成函数文件huaxue.m:
%function yhat=huaxue (beta,x);
%yhat=(beta(4)*x(:,2)-x(:,3)/beta(5))./(1+beta(1)*x(:,1)+...
beta(2)*x(:,2)+beta(3)*x(:,3));
%省略号是用于一行没输完,在第二行上接着输入的需要.
%然后,用nlinfit计算回归系数,用nlparci计算回归系数的置信区间,用nlpredci
%计算预测值及其置信区间,编程如下
x0=[ 1 8.55 470 300 10
2 3.79 285 80 10
3 4.82 470 300 120
4 0.02 470 80 120
5 2.75 470 80 10
6 14.39 100 190 10
7 2.54 100 80 65
8 4.35 470 190 65
9 13.00 100 300 54
10 8.50 100 300 120
11 0.05 100 80 120
12 11.32 285 300 10
13 3.13 285 190 120];
x=x0(:,3:end);
y=x0(:,2);
beta=[0.1 0.05 0.02 1 2]';
%回归系数的初始值,可以任意取,这里是给定的
[betahat,r,j]=nlinfit(x,y,@huaxue,beta);
%beta = nlinfit(X,Y,modelfun,beta0)返回使用指定模型Y的预测变量的响应非线性回归的估计系数向量。
%r,j是下面命令要用的信息
betaci=nlparci(betahat,r,'jacobian',j);
%nlparci---非线性模型参数估计的置信
%ci = nlparci(beta,resid,'covar',sigma)返回ci非线性最小二乘参数估计的95%置信区间。
%在调用之前nlparci,使用nlinfit拟合非线性回归模型并获得系数估计beta,残差resid和估计系数协方差矩阵sigma。
betaa=[betahat,betaci]
%回归系数及其置信区间
[yhat,delta]=nlpredci(@huaxue,x,betahat,r,'jacobian',j)
%nlpredci----非线性模型预测值的置信区间
%y的预测值及其置信区间的半径,置信区间为 yhat ± delta。
nlintool(x,y,'huaxue',beta)
%nlintool(X,y,fun,beta0)是nlinfit函数的图形用户界面,并使用相同的输入参数。
%界面显示针对每个预测变量的拟合响应的图,其他预测变量保持固定。固定值位于每个预测轴下方的文本框中。
%通过键入新值或将绘图中的垂直线拖动到新位置来更改固定值。更改预测变量值时,所有绘图都会更新,以在预测变量空间中的新点处显示模型。
%虚线红色曲线显示该功能的95%同时置信带
资料来自司守奎《数学建模算法与应用》