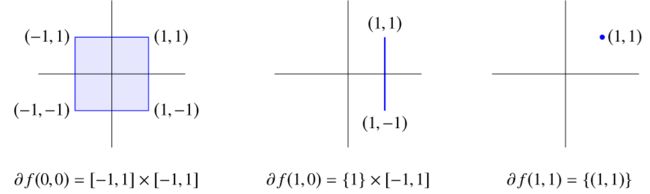凸优化学习笔记16:次梯度 Subgradient
前面讲了梯度下降的方法,关键在于步长的选择:固定步长、线搜索、BB方法等,但是如果优化函数本身存在不可导的点,就没有办法计算梯度了,这个时候就需要引入次梯度(Subgradient),这一节主要关注次梯度的计算。
1. 次梯度
次梯度(subgradient)的定义为
∂ f ( x ) = { g ∣ f ( y ) ≥ f ( x ) + g T ( y − x ) , ∀ y ∈ dom f } \partial f(x)= \{g|f(y)\ge f(x)+g^T(y-x),\forall y\in\text{dom} f \} ∂f(x)={g∣f(y)≥f(x)+gT(y−x),∀y∈domf}
该如何理解次梯度 g g g 呢?实际上经过变换,我们可以得到
[ g − 1 ] ⊤ ( [ y t ] − [ x f ( x ) ] ) ≤ 0 , ∀ ( y , t ) ∈ epi f \left[\begin{array}{c} g \\ -1 \end{array}\right]^{\top}\left(\left[\begin{array}{l} y \\ t \end{array}\right]-\left[\begin{array}{c} x \\ f(x) \end{array}\right]\right) \leq 0, \forall(y, t) \in \operatorname{epi}f [g−1]⊤([yt]−[xf(x)])≤0,∀(y,t)∈epif
实际上这里 [ g T − 1 ] T [g^T \ -1]^{T} [gT −1]T 定义了 epigraph 的一个支撑超平面,并且这个支撑超平面是非垂直的,如下面的图所示
| 光滑函数 | 非光滑函数 |
|---|---|
 |
 |
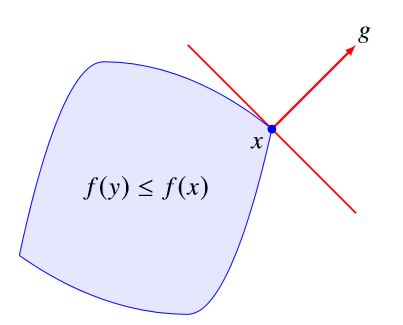
而对于任意的下水平集 { y ∣ f ( y ) ≤ f ( x ) } \{y|f(y)\le f(x)\} {y∣f(y)≤f(x)},都有
f ( y ) ≤ f ( x ) ⟹ g T ( y − x ) ≤ 0 f(y)\le f(x) \Longrightarrow g^T(y-x)\le0 f(y)≤f(x)⟹gT(y−x)≤0
这说明次梯度 g g g 实际上也是下水平集的一个支撑超平面
Remarks:很有意思的一件事是函数的梯度 ∇ f \nabla f ∇f 包含有大量的信息,他的方向代表了函数下降最快的方向,也就是下水平集的法线方向;而他的模长代表了下降的速度, [ ∇ f − 1 ] T [\nabla f\ -1]^T [∇f −1]T 是 epigraph 的法线方向,可以直观想象,如果 ∥ ∇ f ∥ \Vert \nabla f\Vert ∥∇f∥ 越大,那么这个法线方向越趋向于水平,也就是说 epigraph 的标面越趋近于竖直,函数下降速度当然也越快。
每个点的次梯度 ∂ f ( x ) \partial f(x) ∂f(x) 实际上是一个集合,我们先来看这个集合有什么性质呢?我们先列出来然后一一解释:
- 次梯度映射是单调算子
- 如果 x ∈ ri dom f x\in\text{ri dom}f x∈ri domf,则 ∂ f ( x ) ≠ ∅ \partial f(x)\ne \varnothing ∂f(x)=∅,而且是有界、闭的凸集
- x ⋆ = arg min f ( x ) ⟺ 0 ∈ ∂ f ( x ⋆ ) x^\star= \arg\min f(x) \iff 0\in \partial f(x^\star) x⋆=argminf(x)⟺0∈∂f(x⋆)
首先,他是一个 set-valued mapping,而且是一个单调算子,也即
( u − v ) T ( y − x ) ≥ 0 , ∀ u ∈ ∂ f ( y ) , v ∈ ∂ f ( x ) (u-v)^T(y-x)\ge0,\forall u\in\partial f(y),v\in\partial f(x) (u−v)T(y−x)≥0,∀u∈∂f(y),v∈∂f(x)
这个性质很容易由定义导出。
其次,内点处的次梯度总是非空的闭凸集,且有界。
首先可以证明其非空,(默认我们考虑的 f f f 为凸函数)因为函数 f f f 是凸的,其 epigraph 在 ( x , f ( x ) ) (x,f(x)) (x,f(x)) 一定存在一个支撑超平面
∃ ( a , b ) ≠ 0 , [ a b ] T ( [ y t ] − [ x f ( x ) ] ) ≤ 0 ∀ ( y , t ) ∈ epi f \exists(a, b) \neq 0, \quad\left[\begin{array}{l} a \\ b \end{array}\right]^{T}\left(\left[\begin{array}{l} y \\ t \end{array}\right]-\left[\begin{array}{c} x \\ f(x) \end{array}\right]\right) \leq 0 \quad \forall(y, t) \in \text { epi } f ∃(a,b)=0,[ab]T([yt]−[xf(x)])≤0∀(y,t)∈ epi f
由于 t t t 可以趋于 + ∞ +\infty +∞,因此 b ≤ 0 b\le0 b≤0,如果 b = 0 b=0 b=0,由于 x x x 为内点,也很容易导出矛盾,因此可以证明 b < 0 b<0 b<0,于是就可以得到 g = a / ∣ b ∣ g=a/|b| g=a/∣b∣。
其次可以证明其为闭凸集,次梯度还可以表示为
∂ f ( x ) = { g ∣ f ( y ) ≥ f ( x ) + g T ( y − x ) , ∀ y ∈ dom f } = ⋂ y ∈ dom f { g ∣ g T ( y − x ) ≤ f ( y ) − f ( x ) } \begin{aligned} \partial f(x)&= \{g|f(y)\ge f(x)+g^T(y-x),\forall y\in\text{dom} f \} \\ &= \bigcap_{y\in \text{dom}f} \{g|g^T(y-x)\le f(y)-f(x) \} \end{aligned} ∂f(x)={g∣f(y)≥f(x)+gT(y−x),∀y∈domf}=y∈domf⋂{g∣gT(y−x)≤f(y)−f(x)}
这是很多个半空间的交集,因此 ∂ f ( x ) \partial f(x) ∂f(x) 是一个闭的凸集。
最后可以证明次梯度集合是有界的,为了证明他有界,只需证明他的 l ∞ l_\infty l∞ 范数有界即可。可以取
B = { x ± r e k ∣ k = 1 , … , n } ⊂ dom f B=\left\{x \pm r e_{k} | k=1, \ldots, n\right\} \subset \operatorname{dom} f B={x±rek∣k=1,…,n}⊂domf
定义 M = max y ∈ B f ( y ) < ∞ M=\max _{y \in B} f(y)<\infty M=maxy∈Bf(y)<∞,应用次梯度的定义就可以得到
∥ g ∥ ∞ ≤ M − f ( x ) r for all g ∈ ∂ f ( x ) \|g\|_{\infty} \leq \frac{M-f(x)}{r} \quad \text { for all } g \in \partial f(x) ∥g∥∞≤rM−f(x) for all g∈∂f(x)
注意上面的非空、有界、闭凸集都要求 x x x 为定义域的内点,如果是边界上则无法保证。
例子 1:对于凸集 C C C,定义函数 δ C ( x ) = { 0 , x ∈ C + ∞ , x ∉ C \delta_C(x)=\begin{cases}0,&x\in C\\+\infty,&x\notin C\end{cases} δC(x)={0,+∞,x∈Cx∈/C,那么次梯度为
g ∈ ∂ δ C ( x ) ⟺ δ C ( y ) ≥ δ C ( x ) + g T ( y − x ) , ∀ y ∈ C ⟺ g T ( y − x ) ≤ 0 , ∀ y ∈ C ⟺ g ∈ N C ( x ) (normal cone at x ) \begin{aligned} g\in\partial \delta_C(x) &\iff \delta_C(y)\ge \delta_C(x)+g^T(y-x),\forall y\in C \\ &\iff g^T(y-x)\le0, \forall y\in C \\ &\iff g\in N_C(x) \quad \text{ (normal cone at $x$)} \end{aligned} g∈∂δC(x)⟺δC(y)≥δC(x)+gT(y−x),∀y∈C⟺gT(y−x)≤0,∀y∈C⟺g∈NC(x) (normal cone at x)
Remarks:集合 C C C 的 normal cone 的定义为
∀ x ∈ C , N C ( x ) = { g ∣ g T ( y − x ) ≤ 0 , ∀ y ∈ C } \forall x\in C,\quad N_C(x)=\{g| g^T(y-x)\le0,\forall y\in C\} ∀x∈C,NC(x)={g∣gT(y−x)≤0,∀y∈C}
例子 2:函数 f ( x ) = ∣ x ∣ , ∂ f ( x ) = { 1 , x > 0 [ − 1 , 1 ] , x = 0 − 1 x < 0 f(x)=\vert x\vert,\partial f(x)=\begin{cases}1,&x>0\\ [-1,1],&x=0\\ -1&x<0\end{cases} f(x)=∣x∣,∂f(x)=⎩⎪⎨⎪⎧1,[−1,1],−1x>0x=0x<0
例子 3:函数 f ( x ) = ∥ x ∥ 2 , ∂ f ( 0 ) = { g ∣ ∥ g ∥ 2 ≤ 1 } f(x)=\Vert x\Vert_2,\partial f(0)=\{g|\Vert g\Vert_2\le1\} f(x)=∥x∥2,∂f(0)={g∣∥g∥2≤1}
例子 4:对于任意范数 f ( x ) = ∥ x ∥ f(x)=\Vert x\Vert f(x)=∥x∥
∂ f ( x ) = { y ∣ ∥ y ∥ ∗ ≤ 1 , < y , x > = ∥ x ∥ } \partial f(x)=\{y|\Vert y\Vert_*\le1,\left
证明: ∀ g ∈ ∂ f ( x ) \forall g\in\partial f(x) ∀g∈∂f(x),需要 ∥ y ∥ ≥ ∥ x ∥ + g T ( y − x ) ( Δ ) \Vert y\Vert \ge \Vert x\Vert+ g^T(y-x)\quad(\Delta) ∥y∥≥∥x∥+gT(y−x)(Δ)
可以取 y = 2 x ⟹ ∥ x ∥ ≥ g T x y=2x \Longrightarrow \Vert x\Vert \ge g^Tx y=2x⟹∥x∥≥gTx,也可以取 y = 0 ⟹ 0 ≥ ∥ x ∥ − g T x y=0\Longrightarrow 0\ge \Vert x\Vert-g^Tx y=0⟹0≥∥x∥−gTx,因此有 g T x = ∥ x ∥ g^Tx=\Vert x\Vert gTx=∥x∥
由 ( Δ ) (\Delta) (Δ) 式可知应有 ∥ y ∥ ≥ g T y ⟺ ∥ g ∥ ∗ ≤ 1 \Vert y\Vert \ge g^Ty \iff \Vert g\Vert_*\le1 ∥y∥≥gTy⟺∥g∥∗≤1。
2. 次梯度计算
每个点的次梯度是一个集合,这里有两个概念
Weak subgradient calculus:只需要计算其中一个次梯度就够了;
Strong subgradient calculus:要计算出 ∂ f ( x ) \partial f(x) ∂f(x) 中的所有元素。
要想计算出所有的次梯度是很难的,所以大多数时候只需要得到一个次梯度就够了,也就是 Weak subgradient calculus。不过,对于下面这几种特殊情况,我们可以得到完整的次梯度描述(也即 Strong subgradient calculus),他们是:
- 如果 f f f 在 x x x 是可微的,那么 ∂ f ( x ) = { ∇ f ( x ) } \partial f(x)=\{\nabla f(x)\} ∂f(x)={∇f(x)}
- 非负线性组合: f ( x ) = α 1 f 1 ( x ) + α 2 f 2 ( x ) f(x)=\alpha_1 f_1(x)+\alpha_2 f_2(x) f(x)=α1f1(x)+α2f2(x),那么 ∂ f ( x ) = α 1 ∂ f 1 ( x ) + α 2 ∂ f 2 ( x ) \partial f(x)=\alpha_1 \partial f_1(x)+\alpha_2 \partial f_2(x) ∂f(x)=α1∂f1(x)+α2∂f2(x),第二个式子是集合的加法;
- 仿射变换: f ( x ) = h ( A x + b ) f(x)=h(Ax+b) f(x)=h(Ax+b),那么 ∂ f ( x ) = A T h ( A x + b ) \partial f(x)=A^T h(Ax+b) ∂f(x)=ATh(Ax+b)
对于第一条的证明,我们可以取 y = x + r ( p − ∇ f ( x ) ) , p ∈ ∂ f ( x ) y=x+r(p-\nabla f(x)),p\in\partial f(x) y=x+r(p−∇f(x)),p∈∂f(x),那么根据次梯度的定义就有 ∥ p − ∇ f ( x ) ∥ 2 ≤ O ( r 2 ) r → 0 \Vert p-\nabla f(x)\Vert^2\le \frac{O(r^2)}{r}\to0 ∥p−∇f(x)∥2≤rO(r2)→0 随着 r → 0 r\to0 r→0,因此就有 ∇ f ( x ) = p \nabla f(x)=p ∇f(x)=p。
对于第三条的证明,只需要分别证明 A T h ( A x + b ) ⊆ ∂ f ( x ) A^T h(Ax+b) \subseteq \partial f(x) ATh(Ax+b)⊆∂f(x) 和 ∂ f ( x ) ⊆ A T h ( A x + b ) \partial f(x) \subseteq A^T h(Ax+b) ∂f(x)⊆ATh(Ax+b),前者很容易,主要是后者。由于次梯度 d ∈ ∂ f ( x ) d\in \partial f(x) d∈∂f(x) 需要满足 f ( z ) ≥ f ( x ) + d T ( z − x ) ⟺ h ( A z + b ) − d T z ≥ h ( A x + b ) − d T x f(z)\ge f(x)+d^T(z-x) \iff h(Az+b)-d^Tz\ge h(Ax+b)-d^Tx f(z)≥f(x)+dT(z−x)⟺h(Az+b)−dTz≥h(Ax+b)−dTx,也就是说 ( x , A x + b ) (x,Ax+b) (x,Ax+b) 实际上是如下问题的最优解
min h ( z ) − d T y s.t. A y + b = z , z ∈ dom h \begin{aligned} \min \quad& h(z)-d^Ty \\ \text{s.t.}\quad& Ay+b = z,\quad z\in\text{dom}h \end{aligned} mins.t.h(z)−dTyAy+b=z,z∈domh
如果 ( R a n g e ( A ) + b ) ∩ ri dom h ≠ ∅ (Range(A)+b)\cap \text{ri dom}h \ne \varnothing (Range(A)+b)∩ri domh=∅,说明 SCQ 成立,则强对偶性成立,于是根据拉格朗日对偶原理有
∃ λ , s.t. ( x , A x + b ) ∈ arg min { h ( z ) − d T y + λ T ( A y + b − z ) } ⟹ { ∇ y L ( y , z , λ ) = 0 ⟹ 0 ∈ ∂ h ( z ) − λ ∇ z L ( y , z , λ ) = 0 ⟹ d = A T λ \exist \lambda,\text{ s.t. }(x,Ax+b) \in \arg\min \{h(z)-d^Ty+\lambda^T(Ay+b-z)\} \\ \Longrightarrow \begin{cases} \nabla_y L(y,z,\lambda)=0 \Longrightarrow 0\in \partial h(z)-\lambda \\ \nabla_z L(y,z,\lambda)=0 \Longrightarrow d=A^T\lambda \end{cases} ∃λ, s.t. (x,Ax+b)∈argmin{h(z)−dTy+λT(Ay+b−z)}⟹{∇yL(y,z,λ)=0⟹0∈∂h(z)−λ∇zL(y,z,λ)=0⟹d=ATλ
推论:根据第 3 条,可以得到:如果考虑函数 F ( x ) = f 1 ( x ) + . . . + f m ( x ) F(x)=f_1(x)+...+f_m(x) F(x)=f1(x)+...+fm(x),且 ⋂ i ri dom f i ≠ ∅ \bigcap_i \text{ri dom}f_i\ne \varnothing ⋂iri domfi=∅,则 ∂ F ( x ) = ∂ f 1 ( x ) + . . . + ∂ f m ( x ) \partial F(x)=\partial f_1(x)+... + \partial f_m(x) ∂F(x)=∂f1(x)+...+∂fm(x)。(这个实际上可以直接右上面的第二条得到,这里只不过又验证了一次)
证明:我们可以考虑函数 f ( x ) = f 1 ( x 1 ) + . . . + f m ( x m ) f(x)=f_1(x_1)+...+f_m(x_m) f(x)=f1(x1)+...+fm(xm),在定义 A = [ I , . . . , I ] T A=[I,...,I]^T A=[I,...,I]T,那么就有 F ( x ) = f ( A x ) F(x)=f(Ax) F(x)=f(Ax),所以 ∂ F ( x ) = A T ∂ f ( A x ) = [ I . . . I ] [ ∂ f 1 ( x ) , . . . , ∂ f m ( x ) ] T = ∂ f 1 ( x ) + . . . + ∂ f m ( x ) \partial F(x)=A^T \partial f(Ax)=[I\ ...\ I][\partial f_1(x),...,\partial f_m(x)]^T = \partial f_1(x)+... + \partial f_m(x) ∂F(x)=AT∂f(Ax)=[I ... I][∂f1(x),...,∂fm(x)]T=∂f1(x)+...+∂fm(x)。
上面是能获得 Strong subgradient calculus 的几个原则,对于其他情况,我们考虑找到一个次梯度就够了。下面给出一些常见的情况。
点点最大值: f ( x ) = max { f 1 ( x ) , . . . , f m ( x ) } f(x)=\max\{f_1(x),...,f_m(x) \} f(x)=max{f1(x),...,fm(x)},可以定义 I ( x ) = { i ∣ f i ( x ) = f ( x ) } I(x)=\{i|f_i(x)=f(x)\} I(x)={i∣fi(x)=f(x)},那么他的
- weak result:choose any g ∈ ∂ f k ( x ) g\in\partial f_k(x) g∈∂fk(x),其中 k ∈ I ( x ) k\in I(x) k∈I(x)
- strong result: ∂ f ( x ) = conv ⋃ i ∈ I ( x ) ∂ f i ( x ) \partial f(x)=\text{conv}\bigcup_{i\in I(x)}\partial f_i(x) ∂f(x)=conv⋃i∈I(x)∂fi(x)
点点上确界: f ( x ) = sup α ∈ A f α ( x ) f(x)=\sup_{\alpha\in \mathcal{A}} f_\alpha (x) f(x)=supα∈Afα(x),其中 f α ( x ) f_\alpha(x) fα(x) 关于 x x x 是凸的,定义 I ( x ) = { α ∈ A ∣ f α ( x ) = f ( x ) } I(x)=\{\alpha\in\mathcal{A}|f_\alpha(x)=f(x)\} I(x)={α∈A∣fα(x)=f(x)},那么
- weak result:choose any g ∈ ∂ f β ( x ^ ) g\in\partial f_\beta (\hat{x}) g∈∂fβ(x^),其中 f ( x ^ ) = f β ( x ^ ) f(\hat{x})=f_\beta(\hat{x}) f(x^)=fβ(x^)
- strong result: conv ⋃ α ∈ I ( x ) ∂ f α ( x ) ⊆ ∂ f ( x ) \text{conv}\bigcup_{\alpha\in I(x)}\partial f_\alpha(x) \subseteq \partial f(x) conv⋃α∈I(x)∂fα(x)⊆∂f(x),如果要取等号,需要额外的条件
下确界: f ( x ) = inf y h ( x , y ) f(x)=\inf_y h(x,y) f(x)=infyh(x,y),其中 h ( x , y ) h(x,y) h(x,y) 关于 ( x , y ) (x,y) (x,y) 是联合凸的,那么
- weak result: ( g , 0 ) ∈ ∂ h ( x ^ , y ^ ) (g,0)\in \partial h(\hat{x},\hat{y}) (g,0)∈∂h(x^,y^),其中 y ^ = arg min h ( x ^ , y ) \hat{y}=\arg\min h(\hat{x},y) y^=argminh(x^,y)
复合函数: f ( x ) = h ( f 1 ( x ) , . . . , f k ( x ) ) f(x)=h(f_1(x),...,f_k(x)) f(x)=h(f1(x),...,fk(x)),其中 h h h 为单调不减的凸函数, f i f_i fi 为凸函数
- weak result: g = z 1 g 1 + . . . + z k g k , z ∈ ∂ h ( f 1 ( x ) , . . . , f k ( x ) ) , g i ∈ ∂ f i ( x ) g=z_1g_1+...+z_kg_k,z\in\partial h(f_1(x),...,f_k(x)),g_i\in \partial f_i(x) g=z1g1+...+zkgk,z∈∂h(f1(x),...,fk(x)),gi∈∂fi(x)
期望: f ( x ) = E h ( x , u ) f(x)=\mathbb{E}h(x,u) f(x)=Eh(x,u),其中 u u u 为随机变量, h h h 对任意的 u u u 关于 x x x 都是凸的
- weak result:选择函数 u ↦ g ( u ) , g ( u ) ∈ ∂ x h ( x ^ , u ) u\mapsto g(u),g(u)\in \partial_x h(\hat{x},u) u↦g(u),g(u)∈∂xh(x^,u),则 g = E u g ( u ) ∈ ∂ f ( x ^ ) g=\mathbb{E}_u g(u) \in \partial f(\hat{x}) g=Eug(u)∈∂f(x^)
例子 1:picewise-linear function f ( x ) = max i = 1 , . . . , m ( a i T x + b i ) , ∂ f ( x ) = conv { a i ∣ i ∈ I ( x ) } f(x)=\max_{i=1,...,m}(a_i^Tx+b_i),\partial f(x)=\text{conv}\{a_i|i\in I(x)\} f(x)=maxi=1,...,m(aiTx+bi),∂f(x)=conv{ai∣i∈I(x)}
例子 2: l 1 l_1 l1 范数 f ( x ) = ∥ x ∥ 1 = ∣ x 1 ∣ + . . . + ∣ x n ∣ , ∂ f ( x ) = J 1 × ⋯ × J n f(x)=\Vert x\Vert_1=|x_1|+...+|x_n|,\partial f(x)=J_1\times \cdots \times J_n f(x)=∥x∥1=∣x1∣+...+∣xn∣,∂f(x)=J1×⋯×Jn,其中 J k = { [ − 1 , 1 ] x k = 0 1 x k > 0 − 1 x k < 0 J_k=\begin{cases}[-1,1]&x_k=0\\ {1}&x_k>0\\ {-1}&x_k<0 \end{cases} Jk=⎩⎪⎨⎪⎧[−1,1]1−1xk=0xk>0xk<0
例子 3: f ( x ) = λ max ( A ( x ) ) = sup ∥ y ∥ 2 = 1 y T A ( x ) y f(x)=\lambda_{\max}(A(x))=\sup_{\Vert y\Vert_2=1}y^TA(x)y f(x)=λmax(A(x))=sup∥y∥2=1yTA(x)y,其中 A ( x ) = A 0 + x 1 A 1 + ⋯ + x n A n A(x)=A_0+x_1A_1+\cdots +x_nA_n A(x)=A0+x1A1+⋯+xnAn,则取 λ max ( A ( x ^ ) ) \lambda_{\max}(A(\hat{x})) λmax(A(x^)) 对应的单位特征向量 y y y,次梯度可以表示为 ( y T A 1 y , . . . , y T A n y ) ∈ ∂ f ( x ^ ) (y^TA_1y,...,y^TA_ny)\in \partial f(\hat{x}) (yTA1y,...,yTAny)∈∂f(x^)
例子 4:到凸集的欧氏距离 f ( x ) = inf y ∈ C ∥ x − y ∥ 2 = inf y h ( x , y ) f(x)=\inf_{y\in C}\Vert x-y\Vert_2=\inf_{y} h(x,y) f(x)=infy∈C∥x−y∥2=infyh(x,y),其中集合 C C C 为凸集,函数 h h h 关于 ( x , y ) (x,y) (x,y) 是联合凸的。
g = { 0 x ^ ∈ C 1 ∥ y ^ − x ^ ∥ 2 ( x ^ − y ^ ) = 1 ∥ x ^ − P ( x ^ ) ∥ 2 ( x ^ − P ( x ^ ) ) x ^ ∉ C g=\begin{cases}0&\hat{x}\in C\\ \frac{1}{\|\hat{y}-\hat{x}\|_{2}}(\hat{x}-\hat{y})=\frac{1}{\|\hat{x}-P(\hat{x})\|_{2}}(\hat{x}-P(\hat{x})) & \hat{x}\notin C \end{cases} g={0∥y^−x^∥21(x^−y^)=∥x^−P(x^)∥21(x^−P(x^))x^∈Cx^∈/C
例子 5:定义如下凸优化问题的最优解为 f ( u , v ) f(u,v) f(u,v)
minimize f 0 ( x ) subject to f i ( x ) ≤ u i , i = 1 , … , m A x = b + v \begin{aligned} \text{minimize} \quad& f_{0}(x) \\ \text{subject to}\quad& f_{i}(x) \leq u_{i}, \quad i=1, \ldots, m\\ &A x=b+v \end{aligned} minimizesubject tof0(x)fi(x)≤ui,i=1,…,mAx=b+v
如果假设 f ( u ^ , v ^ ) f(\hat{u},\hat{v}) f(u^,v^) 有界且强对偶性成立,那么对于对偶问题如下对偶问题
maximize inf x ( f 0 ( x ) + ∑ i λ i ( f i ( x ) − u ^ i ) + v T ( A x − b − v ^ ) ) subject to λ ⪰ 0 \begin{aligned} \text{maximize} \quad& \inf _{x}\left(f_{0}(x)+\sum_{i} \lambda_{i}\left(f_{i}(x)-\hat{u}_{i}\right)+v^{T}(A x-b-\hat{v})\right) \\ \text{subject to}\quad& \lambda\succeq 0 \end{aligned} maximizesubject toxinf(f0(x)+i∑λi(fi(x)−u^i)+vT(Ax−b−v^))λ⪰0
若其最优解为 ( λ ^ , ν ^ ) (\hat\lambda,\hat\nu) (λ^,ν^),则有 ( − λ ^ , − ν ^ ) ∈ ∂ f ( u ^ , v ^ ) (-\hat\lambda,-\hat\nu)\in \partial f(\hat{u},\hat{v}) (−λ^,−ν^)∈∂f(u^,v^)。
3. 对偶原理与最优解条件
前面我们对于可导函数获得了对偶原理以及 KKT 条件,那如果是不可导的函数呢?我们有
f ( y ) ≥ f ( x ⋆ ) + 0 T ( y − x ⋆ ) for all y ⟺ 0 ∈ ∂ f ( x ⋆ ) f(y) \geq f\left(x^{\star}\right)+0^{T}\left(y-x^{\star}\right) \quad \text { for all } y \quad \Longleftrightarrow \quad 0 \in \partial f\left(x^{\star}\right) f(y)≥f(x⋆)+0T(y−x⋆) for all y⟺0∈∂f(x⋆)

例子:对于优化问题 min f ( x ) , s.t. x ∈ C ⟺ min f ( x ) + δ C ( x ) = F ( x ) \min f(x),\text{s.t. }x\in C \iff \min f(x)+\delta_C(x)=F(x) minf(x),s.t. x∈C⟺minf(x)+δC(x)=F(x),因此
0 ∈ ∂ f ( x ⋆ ) + ∂ δ C ( x ⋆ ) ⟹ ∃ p ∈ ∂ f ( x ⋆ ) , s.t. − p ∈ ∂ δ C ( x ⋆ ) = N C ( x ⋆ ) 0\in \partial f(x^\star)+\partial \delta_C(x^\star) \Longrightarrow \exist p\in\partial f(x^\star),\quad\text{s.t.}-p\in \partial\delta_C(x^\star)=N_C(x^\star) 0∈∂f(x⋆)+∂δC(x⋆)⟹∃p∈∂f(x⋆),s.t.−p∈∂δC(x⋆)=NC(x⋆)
如果 f ∈ C 1 f\in C^1 f∈C1,则有 − ∇ f ( x ⋆ ) ∈ N C ( x ⋆ ) -\nabla f(x^\star)\in N_C(x^\star) −∇f(x⋆)∈NC(x⋆)。
KKT 条件怎么变呢?只需要修改一下梯度条件:
- 原问题可行性 x ⋆ x^\star x⋆ is primal feasible
- 对偶问题可行性 λ ⋆ ⪰ 0 \lambda^\star \succeq0 λ⋆⪰0
- 互补性条件 λ i ⋆ f i ( x ⋆ ) = 0 , i = 1 , . . . , m \lambda_i^\star f_i(x^\star)=0,i=1,...,m λi⋆fi(x⋆)=0,i=1,...,m
- 梯度条件 0 ∈ ∂ f 0 ( x ⋆ ) + ∑ i λ i ⋆ ∂ f i ( x ⋆ ) 0\in \partial f_0(x^\star)+\sum_i \lambda_i^\star \partial f_i(x^\star) 0∈∂f0(x⋆)+∑iλi⋆∂fi(x⋆)
4. 方向导数
方向导数(directional derivative)的定义为
f ′ ( x ; y ) = lim α ↘ 0 f ( x + α y ) − f ( x ) α = lim t → ∞ ( t f ( x + 1 t y ) − t f ( x ) ) \begin{aligned} f^{\prime}(x ; y) &=\lim _{\alpha \searrow 0} \frac{f(x+\alpha y)-f(x)}{\alpha} \\ &=\lim _{t \rightarrow \infty}\left(tf\left(x+\frac{1}{t} y\right)-t f(x)\right) \end{aligned} f′(x;y)=α↘0limαf(x+αy)−f(x)=t→∞lim(tf(x+t1y)−tf(x))
方向导数是齐次的,也即
f ′ ( x ; λ y ) = λ f ′ ( x ; y ) for λ ≥ 0 f'(x;\lambda y)=\lambda f'(x;y) \quad \text{for }\lambda\ge0 f′(x;λy)=λf′(x;y)for λ≥0
对于凸函数,方向导数也可以定义为
f ′ ( x ; y ) = inf α > 0 f ( x + α y ) − f ( x ) α = inf t > 0 ( t f ( x + 1 t y ) − t f ( x ) ) \begin{aligned} f^{\prime}(x ; y) &=\inf _{\alpha > 0} \frac{f(x+\alpha y)-f(x)}{\alpha} \\ &=\inf _{t >0}\left(tf\left(x+\frac{1}{t} y\right)-t f(x)\right) \end{aligned} f′(x;y)=α>0infαf(x+αy)−f(x)=t>0inf(tf(x+t1y)−tf(x))
要证明的话,只需要证明 g ( α ) = f ( x + α y ) − f ( x ) α g(\alpha)=\frac{f(x+\alpha y)-f(x)}{\alpha} g(α)=αf(x+αy)−f(x) 随着 α \alpha α 单调递减有下界。
实际上方向导数定义了沿着 y y y 方向的函数下界,也即
f ( x + α y ) ≥ f ( x ) + α f ′ ( x ; y ) for all α ≥ 0 f(x+\alpha y) \geq f(x)+\alpha f^{\prime}(x ; y) \quad \text { for all } \alpha \geq 0 f(x+αy)≥f(x)+αf′(x;y) for all α≥0
对于凸函数, x ∈ int dom f x\in\text{int dom}f x∈int domf,也有
f ′ ( x ; y ) = sup g ∈ ∂ f ( x ) g T y f^{\prime}(x ; y)=\sup _{g \in \partial f(x)} g^{T} y f′(x;y)=g∈∂f(x)supgTy
也即 f ′ ( x ; y ) f'(x;y) f′(x;y) 是 ∂ f ( x ) \partial f(x) ∂f(x) 的支撑函数
Remarks:需要注意的是负的次梯度方向不一定是函数值下降方向,而只有方向导数 <0 的方向才是函数值下降方向。反例如下图
如果我们想找到下降最快的方向(Steepest descent direction),则需要
Δ x n s d = argmin ∥ y ∥ 2 ≤ 1 f ′ ( x ; y ) \Delta x_{\mathrm{nsd}}=\underset{\|y\|_{2} \leq 1}{\operatorname{argmin}} f^{\prime}(x ; y) Δxnsd=∥y∥2≤1argminf′(x;y)
根据前面的式子我们知道 min f ′ ( x ; y ) = min ∥ y ∥ 2 ≤ 1 sup g ∈ ∂ f ( x ) g T y \min f'(x;y)=\min_{\Vert y\Vert_2\le1}\sup_{g\in\partial f(x)}g^Ty minf′(x;y)=min∥y∥2≤1supg∈∂f(x)gTy,如果假设极大极小可以换序,则可以等价为 sup g inf y g T y = sup g ∈ ∂ f ( x ) − ∥ g ∥ 2 \sup_g \inf_y g^Ty = \sup_{g\in\partial f(x)} -\Vert g\Vert_2 supginfygTy=supg∈∂f(x)−∥g∥2,上面过程可以表述为原问题与对偶问题
minimize f ′ ( x ; y ) subject to ∥ y ∥ 2 ≤ 1 minimize − ∥ g ∥ 2 subject to g ∈ ∂ f ( x ) \begin{aligned} \text{minimize} \quad& f'(x;y) \\ \text{subject to}\quad& \|y\|_{2} \leq 1 \end{aligned} \qquad \begin{aligned} \text{minimize} \quad& -\|g\|_{2} \\ \text{subject to}\quad& g \in \partial f(x) \end{aligned} minimizesubject tof′(x;y)∥y∥2≤1minimizesubject to−∥g∥2g∈∂f(x)
于是就有 f ′ ( x ; Δ x n s d ) = − ∥ g ⋆ ∥ 2 f^{\prime}\left(x ; \Delta x_{\mathrm{nsd}}\right)=-\left\|g^{\star}\right\|_{2} f′(x;Δxnsd)=−∥g⋆∥2, if 0 ∉ ∂ f ( x ) , Δ x n s d = − g ⋆ / ∥ g ⋆ ∥ 2 \text { if } 0 \notin \partial f(x), \Delta x_{\mathrm{nsd}}=-g^{\star} /\left\|g^{\star}\right\|_{2} if 0∈/∂f(x),Δxnsd=−g⋆/∥g⋆∥2,如下图所示
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
凸优化学习笔记 15:梯度方法
凸优化学习笔记 16:次梯度
凸优化学习笔记 17:次梯度下降法