（4）直线的生成之中点画线法

基本原理：
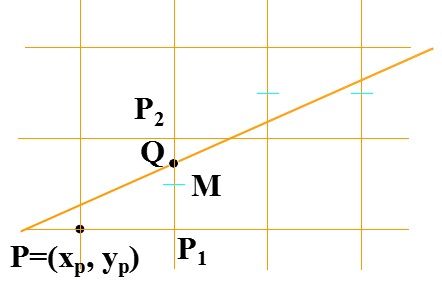
假定直线斜率0

若M在Q上方，则P1离直线更近，应取P1为下一个像素；
若M在Q下方，则P2离直线更近，应取P2为下一个像素；
若M与Q重合，则P1或P2任取一点。
这种以中点M作为判别标志的方法即为中点画线法。

假设直线段的起点为(x1, y1)，终点为(x2, y2)。设直线方程为：F (x, y)= ax + by + c ＝0
其中：a = y1 - y2，b = x2 - x1，c = x1 y2 - x2 y1

F(x,y)= 0时，则点在直线上；
当F(x,y)> 0时，则点在直线上方；
当F (x,y)< 0时，则点在直线下方。

要判断M在Q的上方还是下方，只需把M代入F(x, y)，并判断它的符号

构造判别式：
         d＝F(M)=F(xp+1, yp+0.5)=a(xp+1)+b(yp+0.5)+c

若d<0，M在直线（Q点）下方，则取右上方的P2点作为下一个像素；
若d>0，M在直线（Q点）上方，则取正右方的P1点作为下一个像素；
若d=0，选P1点或P2点均可，约定取正右方P1点。 

d是xp和yp的线性函数，可采用增量计算，以提高运算效率。

当d≥0时，取正右方像素P1，则再下一个像素的判别式为：
                d1 = F(xp+2, yp+0.5)= a(xp+2)+b(yp+0.5)+c 
                     = a(xp+1)+b(yp+0.5)+c+a = d + a
所以此时 d 的增量为 a

当d<0时，取右上方像素P2，则再下一个像素的判别式为：
                 d2 = F(xp+2, yp+1.5)=a(xp+2)+b(yp+1.5)+c 
                     = a(xp+1)+b(yp+0.5)+c+a+b = d + a + b
所以此时 d 的增量为 a+b

d 的初始值问题：
假设直线的第一个像素为左端点(x1, y1)，则相应的判别式为
                d0 = F(x1+1, y1+0.5)=a(x1+1)+b(y1+0.5)+c
                     = (ax1+by1+c)+a+0.5b = F(x1, y1)+a+0.5b
所以左端点(x1, y1)在直线上
所以 F (x1, y1) = 0，即 d 的初始值 d0 = a+0.5b

中点画线法的算法步骤（0≤k≤1）：
1. 输入直线段的两个端点P1(x1, y1)和P2(x2, y2)。
2. 初始化：a，b，d=a+0.5b，x=x1，y=y1，画点(x, y)。
3. 若x 4. 判断d的符号；若d<0，则(x, y)更新为(x+1, y+1)，d更新为d+a+b；否则(x, y)更新为(x+1, y)，d更新为d+a。
5. 画点(x, y)，返回3。

改进：用2d代替d的中点画线法的算法步骤（0≤k≤1 ）
1. 输入直线段的两个端点P1(x1, y1)和P2(x2, y2)。
2. 初始化：a，b，d=2a+b，x=x1，y=y1，画点(x, y)。
3. 若x 4. 判断d的符号：若d<0，则(x, y)更新为(x+1, y+1)，d更新为d+2a+2b；否则(x, y)更新为(x+1, y)，d更新为d+2a。
5. 画点(x, y)，返回3。

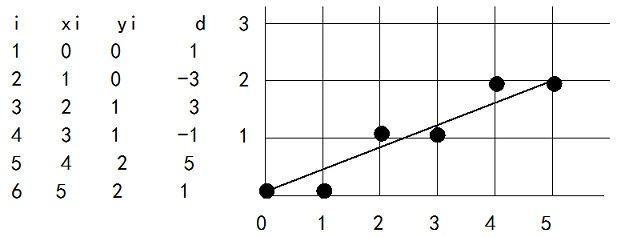
例：用中点画线法画直线段 P1(0, 0)—P2(5, 2)
a=y1-y2=-2      b=x2-x1=5
d0=2a+b=1     d1=2a=-4     d2=2(a+b)=6

代码（0

void MPLine(int x1,int y1,int x2,int y2,int color){
	int x,y,a,b,c,d,d1,d2;
	a=y1-y2;b=x2-x1;
	y=y1;
	d=2*a+b;d1=2*a;d2=2*(a+b);
	putpixel(x,y,color);
	k=1.0*(y2-y1)/(x2-x1);
	for(x=x1;x<=x2;x++){
		if(d<0){
			y++;
			d+=d2;
		}else{
			d+=d1;
		}
		putpixel(x,y,color);
	}
}