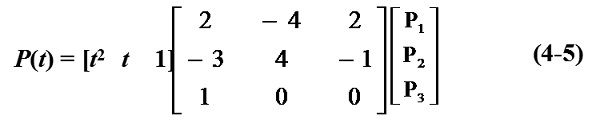（26）二次插值样条曲线

在拟合生成样条曲线的众多方法中，首先来讨论用插值方法生成通过给定离散型值点的二次样条曲线，即抛物样条曲线。

已知不在同一直线上的三点P₁、P₂、P₃，要求通过给定的这三点定义一条抛物线。

                    

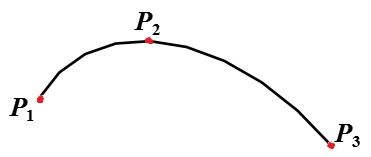
二次样条曲线的参数化表达式为：

           P(t) = A₁ + A₂t + A₃t²    (0≤t≤1)          (4-1)

A₁、A₂、A₃为表达式的系数，且是向量形式。若是二维平面曲线，则为二维向量；若是三维空间曲线，则为三维向量。

确定系数A₁、A₂、A₃的三个独立条件：

该曲线过P₁、P₂、P₃三个点，并且：

①曲线段以P₁点为始点。即当参变量t = 0时，曲线过P₁点；

②曲线段以P₃点为终点。即当参变量t = 1时，曲线过P₃点；

③当参变量t = 0.5时，曲线过P₂点，且切矢量等于P₃–P₁。

                

根据以上设定的三个独立条件，可以列出方程组：

       t = 0：   P(0) = A₁ = P₁

       t = 1：   P(1) = A₁+ A₂+ A₃ = P₃          (4-2)

       t = 0.5：  P(0.5) = A₁+0.5A₂+0.25A₃ = P₂ 

解得三个系数A₁、A₂、A₃分别为： 

        A₁ = P₁

      A₂ = 4P₂– P₃– 3P₁                (4-3)

      A₃ = 2P₁+ 2P₃– 4P₂

把求出的三个系数代入到式(4-1)中，可得：

     P(t)= A₁ + A₂t + A₃t²

      = P₁ +(4P₂ – P₃ – 3P₁)t + (2P₁+2P₃ – 4P₂)t²       (0≤t≤1)

      = (2t² – 3t + 1)P₁ + (–4t² + 4t)P₂ + (2t² – t)P₃            (4-4)

把式(4-4)改写成矩阵形式为：

        

式(4-5)中的P(t)是一个点向量，在二维平面上它包含了两个坐标值[x(t), y(t)]，故式(4-5)的直观形式可以写成如下形式：

       

二次插值样条曲线的加权合成 

设有一个离散型值点列Pi(i = 1, 2, …,n)，可以按式(4-5) 每经过相邻三点作一段抛物线，由于有n个型值点，所以像这样的抛物线段一共可以作出n–2条。

            

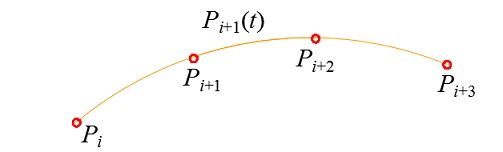
第i条抛物线段经过P_i、P_i+1、P_i+2三点，其表达式为：

   S_i(t_i)=(2t_i²–3t_i+1)P_i+(4t_i–4t_i²)P_i+1+(2t_i²–t_i)P_i+2   (0≤t_i≤1)    (4-7)

第i+1条抛物线段经过P_i+1、P_i+2、P_i+3三点，其表达式为：

   S_i+1(t_i+1)=(2_ti+1²–3t_i+1+1)P_i+1+(4t_i+1–4t_i+1²)P_i+2+(2t_i+1²–t_i+1)P_i+3   (0≤t_i+1≤1)   (4-8) 

         

经过四点所画出的两条抛物线段S_i(t_i)和S_i+1(t_i+1)的图形

一般来说，每两段曲线之间的搭接区间，两条抛物线是不可能重合的。Si和Si+1两条抛物线在Pi+1和Pi+2两点之间为搭接区间，在该区间内，Si和Si+1不太可能自然地重合成一条曲线。

对于拟合曲线来说，整个型值点列必须只能用一条光滑曲线连接起来。因此，在Si和Si+1两条曲线的搭接区间内，必须有一个方法能够让它们按照一定的法则结合成一条曲线，这样结合的方法就是加权合成。  

 在加权合成过程中，首先要选择两个合适的权函数。这里选择的两个权函数分别设为f(T)和g(T)，加权合成后的曲线用Pi+1(t)表示，则：

          P_i+1(t) = f(T)·S_i(t_i) + g(T)·S_i+1(t_i+1)           (4-9)

在抛物样条曲线中，权函数f(T)和g(T)都是简单的一次函数，且它们之间存在互补性。它们分别为：
                         f(T) = 1–T
                         g(T) = T                    (0≤T≤1) 

这样，式(4-9)可改写为：

             P_i+1(t) = (1–T)·S_i(t_i) +T·S_i+1(t_i+1)           (4-10)

式(4-10)中包含了三个参变量T、ti、ti+1，必须要统一这三个参变量： 

         

这里选择 t 作为统一后的参变量，把原有的三个参变量T、t_i、t_i+1都化成唯一含有t的形式，并给t 规定一个合适的取值范围。假设t的取值范围为：0≤t≤0.5，则三个参变量可统一形式为：

                             T = 2t
                             ti = 0.5 + t          0≤t≤0.5
                             ti+1 = t 

则式(4-10)可根据新的参变量t 改写成如下形式：

           P_i+1(t) = (1–2t)·S_i(t + 0.5) + 2t·S_i+1(t)          (4-11)

其中：

     S_i(t+0.5) = (2t²–t)P_i+(1–4t²)P_i+1+(2t²+t)P_i+2

     S_i+1(t) = (2t²–3t+1)P_i+1+(4t–4t²)P_i+2+(2t²–t)P_i+3 

把以上两式代入式(4-11)，展开、整理后可得：

    P_i+1(t) = (–4t³ + 4t² –t)P_i + (12t³–10t² +1)P_i+1                                     + (–12t³ + 8t² + t)P_i+2 + (4t³– 2t²)P_i+3 (i = 1，2，…， n–3) (0≤t≤0.5)      (4-12)

           

假如一个离散点列Pi具有n个型值点，即i=1，2，…，n。那么根据式(4-12)，加权合成后可以生成n–3段抛物样条曲线。即式(4-12)中的i的取值范围为：i =1～n–3。

 

二次插值样条曲线的端点条件

根据式(4-12)，在全部型值点列 Pi (i=1，2，…，n) 中，只能得到n–3段曲线。但n个型值点之间应该有n–1个区段。主要是因为点列的首、尾两段曲线P1P2和Pn–1Pn段，由于缺乏连续相邻的四点这样的条件而无法产生。

为了要产生首尾两段曲线，可以在原点列的两端各增加一个辅助点P0和Pn+1。    

       

增加点P₀和点P_n+1的三种方法：

① 已知两端的切矢P'₁和P'_n

在由P₁、P₂、P₃三点所确定的抛物线中，过P₂点曲线的切矢

                P' ₂ = P₃–P₁        即：P₁ = P₃–P'₂

根据上面的原理可得：

               P'₁ = P₂–P₀            ∴ P₀= P₂–P'₁

               P'_n = P_n+1–P_n–1     ∴ P_n+1 = P_n–1+ P'_n

这种端点情况，一般适用于所求的曲线要和已经存在的曲线或直线相连接。 

②自由端条件

让补点P₀ 和P_n+1与原两端点P₁和P_n分别重合，即：

                    P₀ = P₁

                    P_n+1 = P_n 

这种补点方法称为自由端条件，该方法一般适用于对曲线的两端没有特殊要求。

③ 形成封闭曲线

在n个型值点之间形成封闭曲线，要生成n个曲线段，而不是原来的n–1段。所以在补点中要增加3个点，首先让首尾两点重合，然后各向前后延长一点，即：

            P_n+1 = P₁

            P₀ = P_n

            P_n+2 = P₂ 

 

二次插值样条曲线的性质

二次插值样条曲线的连续性问题：

1、相邻两曲线段P_i+1(t)和P_i+2(t)在型值点P处相连。并且P_i+1(t)在P点处的参变量t =0.5，而P_i+2(t)在P点处的参变量t =0。

2、满足C1连续，即P_{i+1 ’}(0.5) = P_{i+2 ’}(0) = P_i+3-P_i+1

               

P_i+1(t) = (-4t³ + 4t² – t)P_i+ (12t³ – 10t² + 1)P_i+1 

            + (-12t³ + 8t² + t)P_i+2 + (4t³ – 2t²)P_i+3             (0≤t≤0.5) 

P_i+1’(t) = (-12t² + 8t – 1)P_i + (36t² – 20t)P_i+1 

            +(-36t² + 16t + 1)P_i+2 + (12t² – 4t)P_i+3

当t = 0.5时：P_i+1’(0.5) = P_i+3 – P_i+1

P_i+2’(t) = (-12t² + 8t – 1)P_i+1 + (36t² – 20t)P_i+2 

                    +(-36t² + 16t + 1)P_i+3 + (12t² – 4t)P_i+4

当t = 0时：P_i+2’(0) = P_i+3 – P_i+1

因此得出P_{i+1 ’}(0.5) = P_{i+2 ’}(0) ，说明可以达到C¹连续。