组合数和组合数取模

【n!】

1.求n!中有多少个质因子p

最直观的想法是计算从 $1\sim n$ 的每个数各有多少个质因子 $p$，然后将结果累加，时间复杂度为$O(nlogn)$，代码如下：

//计算n!中有多少个质因子p
int cal(int n, int p)
{
	int ans = 0;
	for(int i = 2;i <= n; i++)	//遍历2~n
	{
		int temp = i;
		while(temp % p == 0)	//只要temp还是p的倍数
		{ 
			ans++;  //p的个数加1
			temp /= P;  //temp除以p
		}
	}
	return ans;
}

但是这种做法对 $n$ 很大的情况 (例如 $n=10^{18}$) 是无法承受的，我们需要寻求速度更快的方法。

现在考虑 $10!$ 中质因子 $2$ 的个数，如下图所示。

显然，$10!$ 中有因子 $2^1$ 的数的个数为 $5$，有因子 $2^2$ 的数的个数为 $2$，有因子 $2^3$ 的数的个数为 $1$，因此 $10!$ 中质因子 $2$ 的个数为 $5+2+1=8$。

仔细思考可以发现此过程可以推广为：$n!$ 中有 $(\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}...)$ 个质因子 $p$，其中除法均为向下取整。

于是，便得到了 $O(logn)$ 的算法，代码如下：

//计算n!中有多少个质因子p
int cal(int n, int p)
{
	int ans = 0;
	while(n)
	{
		ans += n / p;	//累加n/p^k 
		n /= p;  		//相当于分母多乘一个p
	}
	
	return ans;
}

从另一个角度理解，$n!$ 中质因子 $p$ 的个数，实际上等于 $1\sim n$ 中 $p$ 的倍数的个数 $\frac{n}{p}$ 加上 $\frac{n}{p}!$ 中质因子 $p$ 的个数。

于是，递归版本如下：

//计算n!中有多少个质因子p
int cal(int n, int p) 
{
	if(n < p) return 0;  		//n
	return n/p + cal(n/p, p);  //返回n/p加上(n/p)!中质因子p的个数
}

2.求n!的末尾有多少个零

利用上述算法，可以很快计算出 n! 的末尾有多少个零：由于末尾 $0$ 的个数等于 $n!$ 中因子 $10$ 的个数，而这又等于 $n!$ 中质因子 $5$ 的个数，因此只需要 $cal(n,5)$ 就可以得到结果。

【组合数】

1.通过定义式直接计算

$C_n^m=\frac{n!}{m!(n-m)!}$，只需要先计算 $n!$，然后令其分别除以 $m!$ 和 $(n-m)!$ 即可。

但由于阶乘相当庞大，即便使用 long long 存储也只能承受 $n\le 20$ 的数据范围。

long long C(long long n, long long m)
{
	long long ans = 1;
	for(long long i = 1; i <= n; i++)
		ans *= i;
	
	for(long long i = 1; i <= m; i++)
		ans /= i;
	
	for(long long i = 1; i <= n-m; i++)
		ans /= i;

	return ans;
}

2.通过递推公式计算

$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$

直观上看，公式总是把 $n$ 减 $1$，而把 $m$ 保持原样或是减 $1$，这样这个递推式最终总可以把 $n$ 和 $m$ 变成相同或是让 $m$ 变为 $0$。而由定义可知，$C_n^0=C_n^n=1$，这正好可以作为递归边界。

long long C(long long n, long long m)
{
	if(m==0||m==n)	return 1;
	return	C(n-1, m) + C(n-1, m-1);
}

开一个备忘录数组，防止重复计算：

long long res[67][67] = {0};
long long C(long long n, long long m)
{
	if(m==0||m==n)	return 1;
	if(res[n][m] != 0)	return res[n][m];
	return res[n][m] = C(n-1, m) + C(n-1, m-1);	//赋值给res[n][m]并返回 
}

或者是下面这种把整张表都计算出来的递推代码：

const int n = 60;
long long res[67][67] = {0};
void calC()
{
	for(int i = 0; i <= n; i++)
		res[i][0] = res[i][i] = 1;	//初始化边界
		
	for(int i = 2; i <= n; i++)
	{
		for(int j = 0; j <= i / 2; j++)
		{
			res[i][j] = res[i-1][j] + res[i-1][j-1];	//递推计算C(i,j)
			res[i][i-j] = res[i][j]; 	//C(i,i-j) = C(i,j)			
		}	
	}
}

3.通过定义式的变形来计算

$C_n^m=\frac{n!}{m!(n-m)!}$ 可化简得 $C_n^m=\frac{(n-m+1)\ast (n-m+2)\ast ...(n-m+m)}{1\ast 2\ast ..\ast m}$

观察上式可以发现，分子和分母的项数恰好均为 $m$ 项，因此不妨按如下方式计算：

很容易证明每次除法都是整数，因此，用这种边乘边除的方法可以避免连续乘法的溢出问题。

时间复杂度为 $O(m)$，代码如下：

long long C(long long n, long long m)
{
	long long ans = 1;
	
	for(long long i = 1; i <= m; i++)
		ans = ans * (n - m + i) / i;	//注意一定要先乘再除 
	return ans;
}

4.说明

第三种方法有可能在最后一个乘法时溢出，因此实际上比方法二支持的数据范围小一点，然而差别不大。例如方法二在 $n=67、m=33$ 时开始溢出，而方法三是在 $n=62、m=31$ 时开始溢出。不过不管怎样，优秀的时间复杂度让它可以代替方法一。

至此已经介绍了三种计算组合数 $C_n^m$ 的方法，但是一旦 $C_n^m$ 本身超过了 long long 型，那么讨论就会失去意义。在这种情况下，可以使用大整数运算来解决这个问题，但是这不是讨论的关键。

一般来说，常见的情况是让运算结果对一个正整数 $p$ 取模，也就是求 $C_n^m\%p$，这才是所要讨论的内容。

【组合数取模】

1.通过递推公式计算

可以很好地支持 $m\le n\le 1000$ 的情况，并且对 $p$ 的大小和素性没有额外限制。

递归代码：

int res[1010][1010] = {0};
int C(int n, int m, int p)
{
	if(m==0||m==n)	return 1;	//C(n,0) = C(n,n) = 1  
	if(res[n][m] != 0)	return res[n][m];	//已经有值 
	return res[n][m] = (C(n-1, m) + C(n-1, m-1)) % p;	//赋值并返回 
}

递推代码：

void calC()
{
	for(int i=0;i<=n;i++)
		res[i][0] = res[i][i] = 1;	//初始化边界
		
	for(int i=2;i<=n;i++)
	{
		for(int j=0;j<=i/2;j++)
		{
			res[i][j] = (res[i-1][j] + res[i-1][j-1])%p;	//递推计算C(i,j)
			res[i][i-j] = res[i][j]; 	//C(i,i-j) = C(i,j)			
		}	
	}
}

2.根据定义式计算

将组合数 $C_n^m$ 进行质因子分解，假设分解结果为 $C_n^m=p_1^{c_1}{p}_2^{c_2}...p_k^{c_k}$，那么 $C_n^m\%p$ 就等于 $p_1^{c_1}{p}_2^{c_2}...p_k^{c_k}\%p$，于是可以用快速幂来计算每一组 $p_i^{c_i}\%p$，然后相乘取模就能得到最后的结果。

怎样将 $C_n^m$ 进行质因子分解呢？只要遍历不超过 $n$ 的所有质数 $p_i$ ，然后计算出 $n!$、$m!$、$(n-m)!$ 中分别含质因子 $p_i$ 的个数 $x、y、z$，就可以知道 $C_n^m$ 进行质因子 $p_i$ 的个数为 $x-y-z$

时间复杂度为 $O(klogn)$，其中 $k$ 为不超过 $n$ 的质数个数。由此可知，能够支持 $m\le n\le 10^6$ 的数据范围，并且对 $p$ 的大小和素性没有额外限制。

//使用筛法得到素数表prime，注意表中最大素数不得小于n
int prime[maxn];

//计算C(n,m)%p
int C(int n, int m, int p) 
{
	int ans = 1;
	//遍历不超过n的所有质数
	for(int i = 0; prime[i] <= n; i++) 
	{
		//计算C(n,m)中prime[i]的指数c，cal(n,k)为n!中含质因子k的个数
		int c = cal(n, prime[i]) - cal(m, prime[i]) - cal(n-m, prime[i]);
		//快速幂计算prime[i]^c%p
		ans = ans * binaryPow(prime[i], c, p) % p;
	}
	return ans;
}

3.通过定义式的变形来计算

下面分三种情况讨论：

（1） m < p m

m<p，且 $p$ 是素数

除法不能直接模上 $p$，但如果 $p$ 是素数，可以使用扩展欧几里得算法或者费马小定理求出 $i$ 模 $p$ 的逆元，然后将除法取模转化为乘法取模来解决。此时必须满足 m < p m

m<p，否则中间过程求逆元可能失效（即 $i$ 是 $p$ 的倍数的情况）。

时间复杂度为 $O(mlogm)$，其中 $O(logm)$ 是计算逆元的复杂度。

能支持 $m\le 10^5$ 的情况（如果设备允许 $m\le 10^6$ 问题也不大），且对 $n$ 和 $p$ 的范围限制不大（例如 $n,p\le 10^9$ 是可行的），但是 $p$ 必须是素数。

//求C(n,m)%p，且m
int C(int n, int m, int P)
{
	int ans = 1;
	for(int i = 1; i <= m; i++)
	{
		ans = ans * (n - m + i) % p;
		ans = ans * inverse(i, p) % p;		//求i模p的逆元
	}
	return ans;
}

（2）$m$ 任意，且 $p$ 是素数

由于引入了 $numP$ 的计算过程，这种做法的时间复杂度为 $O(mlogn)$。

能支持 $m\le 10^5$ 的情况（如果设备允许 $m\le 10^6$ 问题也不大），且对 $n$ 和 $p$ 的范围限制不大（例如 $n,p\le 10^9$ 是可行的），但是 $p$ 必须是素数。

//求C(n,m)%p
int C(int n, int m, int p)
{
	//ans存放计算结果, numP统计分子中的p比分母中的p多几个
	int ans = 1, numP = 0;
	for(int i = 1; i <= m; i++)
	{
		int temp = n - m + i;  //分子
		while(temp % p == 0)	//去除分子中的所有p, 同时累计numP
		{
			numP++;
			temp /= p;
		}
		ans = ans * temp % p;	//乘以分子中除了P以外的部分
		
		temp = i;  //分母
		while(temp % p == 0) //去除分母中的所有p, 同时减少numP
		{
			numP--;
			temp /= p;
		}
		ans = ans * inverse(temp, p) % p;	//除以分母中除了p以外的部分
	}
	
	if(numP > 0) return 0;  //分子中p的个数多于分母，直接返回0
	else return ans;  		//分子中p的个数等于分母，返回计算的结果
}

（3）$m$ 任意，$p$ 可能不是素数

4.Lucas定理

Lucas定理意味着将 $C_n^m\%p$ 分解为 $O(logn)$ 级别个小组合数的乘积的模。

显然，分解出的小组合数 $C_{n_i}^{m_i}$ 均满足 n i < p n_i

ni​<p，因此，Lucas定理非常适合处理 $p\le 10^5$ 级别的大组合数取模问题，此时能够支持 long long 级别的 $n$ 和 $m$，也就是 $m\le n\le 10^{18}$ 级别的数据范围。唯一的要求是 $p$ 是素数。

int Lucas(int n, int m)
{
	if(m == 0) return 1;
    return C(n % p, m % p) * Lucas(n / p, m / p) % p;
}

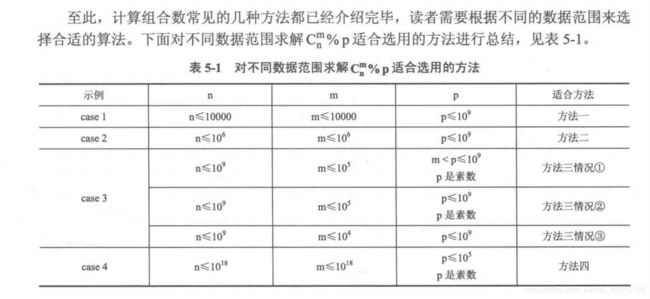
5.总结