竞赛图(有向完全图)上哈密顿路径的若干性质(BZOJ4727 [POI2017]Turysta 题解)
一.竞赛图与哈密顿路径的定义.
竞赛图:竞赛图是一张有向无环图 G = { V , E } G=\{V,E\} G={V,E},满足有 ∣ E ∣ = ∣ V ∣ ( ∣ V ∣ − 1 ) |E|=|V|(|V|-1) ∣E∣=∣V∣(∣V∣−1)边且两点之间仅有一条边,也就是说两点之间有且仅有一条边.
哈密顿路径:一条经过 n n n个点的简单路径,即不能重复经过一个点.
哈密顿回路:一条哈密顿回路相当于一条哈密顿路径的终点与起点也通过一条边连起来.
性质0:对于一张 n n n个点的强连通分量最大为 1 1 1的竞赛图,则每一个点的入度和出度必然能组成一个 0 0 0到 n − 1 n-1 n−1的排列.
也就是说一张无环的竞赛图长这样子:
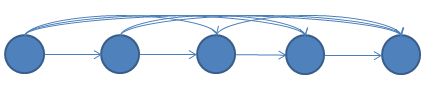
二.竞赛图与哈密顿路径.
关于竞赛图会有很多性质,主要是竞赛图上的哈密顿路的性质.
性质1:一张竞赛图必然有哈密顿路.
证明:
考虑数学归纳法:
1.显然 n = 1 , 2 , 3 n=1,2,3 n=1,2,3时候的竞赛图上均有一条哈密顿路径.
2.若结论在 n − 1 ( n > 3 ) n-1(n>3) n−1(n>3)的时候成立,考虑加入一个点,分三种情况讨论:
情况1.若原哈密顿路的终点有一条向当前加入点的连边,则直接让当前点成为新哈密顿路的终点.
情况2.若当前点向原哈密顿路的起点有连边,则直接让当前点成为新哈密顿路的起点.
情况3.若均不满足,我们将当前点向原哈密顿路中每一个点连的边看成一个 01 01 01序列,若是从当前点出发的边看成 0 0 0,连向当前点的看成 1 1 1,则 01 01 01序列必然以 1 1 1开头以 0 0 0结尾.显然现在必然有两个相邻项为 10 10 10,把当前点加入这两项的中间即可.
证毕.
性质2:一张强连通竞赛图必然有一条哈密顿回路.
证明:
首先根据性质1,一张竞赛图 G = { V , E } G=\{V,E\} G={V,E}有一条哈密顿路径.
考虑在这条哈密顿路径基础上构造哈密顿回路.
设当前哈密顿路径的开头为 h d hd hd,先找到 h d hd hd之后第一个向 h d hd hd有连边的点 t l tl tl,显然从 h d hd hd到 t l tl tl构成了一条回路,我们称之为一个“环”.
考虑枚举在原哈密顿路上 t l tl tl之后的点 i i i,若当前环上不存在一个点 j j j能够满足存在边 ( i , j ) ∈ E (i,j)\in E (i,j)∈E,则根据当前竞赛图的强连通性,后面必然存在点 i i i满足当前环上存在点 j j j使得边 ( i , j ) ∈ E (i,j)\in E (i,j)∈E.
否则,设点 j j j为存在边 ( i , j ) (i,j) (i,j)的最接近 h d hd hd的点,则设 j j j在当前哈密顿回路的上一个点为 k k k, t l tl tl的下一个点为 t t t.
显然当前竞赛图必然存在边 ( k , t ) ∈ E (k,t)\in E (k,t)∈E(若不存在,则说明存在边 ( t , k ) ∈ E (t,k)\in E (t,k)∈E,此时当前环应该是 h d hd hd到 t t t,与条件矛盾),此时必然可以构造一个更大的环 h d → k → t → i → j → t l → h d hd\rightarrow k\rightarrow t\rightarrow i\rightarrow j\rightarrow tl\rightarrow hd hd→k→t→i→j→tl→hd.
综上,必然可以在一张强连通竞赛图上构造一条哈密顿回路.
证毕.
性质3:一张竞赛图若要有哈密顿回路,必要条件为此竞赛图强连通.
不强连通怎么从终点跑回起点…
性质2与性质3合起来就是说明竞赛图有哈密顿回路 ⇔ \Leftrightarrow ⇔竞赛图强连通.
三.例题与代码.
例题:BZOJ4727.
题目大意:给定一张 n n n个点的竞赛图,求这张竞赛图中从每个点开始的最长路径,并输出长度与方案.
1 ≤ n ≤ 2000 1\leq n\leq 2000 1≤n≤2000.
首先,很容易通过性质1的证明过程构造一张竞赛图的哈密顿路径,也很容易通过性质2的证明过程用一张强连通竞赛图的哈密顿路径构造它的哈密顿回路.
然后我们只需要把这张竞赛图SCC缩点,根据性质0,容易发现一条最长的路径一定是从当前SCC开始不断往下一个SCC走.
而对于每一个SCC内部,我们可以构造它的哈密顿回路.
而对于当前SCC和下一个SCC,容易发现当前SCC的任意一个点都可以走到下一个SCC的任意一个点.所以,最终的路径只需要通过从当前点所在的SCC开始把接下来所有的SCC拼接起来就好了.
时间复杂度 O ( n 2 ) O(n^2) O(n2).
代码如下:
#include