笛卡尔坐标系
笛卡尔坐标系
在数学里,笛卡尔坐标系 (Cartesian coordinate system),亦称直角坐标系,是一种正交坐标系。二维的直角坐标系是由两条相互垂直、相交于原点的数线构成的。在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的。
直线标准式 a x + b y + c = 0 ax + by + c = 0 ax+by+c=0、斜截式 y = m x + k y = mx + k y=mx+k。一个圆,半径为 r r r,圆心位于 ( a , b ) (a, b) (a,b)。圆圈以 ( x − a ) 2 + ( y − b ) 2 = r 2 (x - a)^{2} + (y - b)^{2} = r^{2} (x−a)2+(y−b)2=r2 表示。
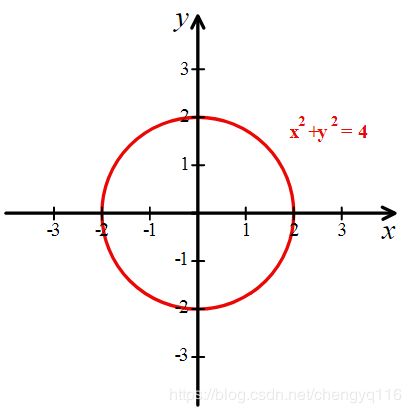
图 1 红色的圆圈,半径是 2,圆心位于直角坐标系的原点。圆的方程为 x 2 + y 2 = 4 x^2 + y^2 = 4 x2+y2=4。
1. 二维坐标系统
二维的直角坐标系通常由两个互相垂直的坐标轴设定,通常分别称为 x-轴和 y-轴。两个坐标轴的相交点,称为原点,通常标记为 O,既有零的意思,又是英语 Origin 的首字母。每一个轴都指向一个特定的方向。这两个不同线的坐标轴,决定了一个平面,称为 xy-平面,又称为笛卡尔平面。
通常两个坐标轴只要互相垂直,其指向何方对于分析问题是没有影响的,但习惯性地,x-轴被水平摆放,称为横轴,通常指向右方。y-轴被竖直摆放而称为纵轴,通常指向上方。两个坐标轴这样的位置关系,称为二维的右手坐标系,或右手系。
如果把这个右手系画在一张透明纸片上,则在平面内无论怎样旋转它,所得到的都叫做右手系;但如果把纸片翻转,其背面看到的坐标系则称为左手系。这和照镜子时左右对调的性质有关。
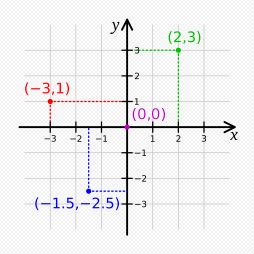
图 2 直角坐标系。图中四点的坐标分别为,绿点: ( 2 , 3 ) (2, 3) (2,3),红点: ( − 3 , 1 ) ( -3, 1) (−3,1),蓝点: ( − 1.5 , − 2.5 ) (-1.5, -2.5) (−1.5,−2.5),紫点: ( 0 , 0 ) (0, 0) (0,0)。
为了要知道坐标轴的任何一点,离原点的距离。我们可以刻画数值于坐标轴。那么,从原点开始,往坐标轴所指的方向,每隔一个单位长度,就刻画数值于坐标轴。这数值是刻画的次数,也是离原点的正值整数距离;同样地,背着坐标轴所指的方向,我们也可以刻画出离原点的负值整数距离。称 x-轴刻画的数值为 x-坐标,又称横坐标,称 y-轴刻画的数值为 y-坐标,又称纵坐标。
在这里,这两个坐标都是整数,对应于坐标轴特定的点。按照比例,我们可以推广至实数坐标和其所对应的坐标轴的每一个点。这两个坐标就是直角坐标系的直角坐标,标记为 ( x , y ) (x, y) (x,y)。
任何一个点 P 在平面的位置,可以用直角坐标来表达。只要从点 P 画一条垂直于 x-轴的直线。从这条直线与 x-轴的相交点,可以找到点 P 的 x-坐标。同样地,可以找到点 P 的 y-坐标。这样,我们可以得到点 P 的直角坐标。图 3,点 P 的直角坐标是 ( 3 , 5 ) (3, 5) (3,5)。
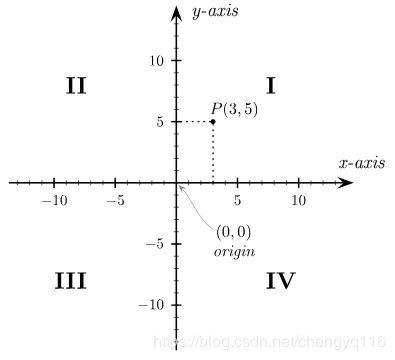
图 3 直角坐标系的四个象限,按照逆时针方向,从象限 I I I 到象限 I V IV IV。坐标轴的头部象征着,往所指的方向,无限的延伸。
图 3 直角坐标系的两个坐标轴将平面分成了四个部分,称为象限,分别用罗马数字编号为 I ( + , + ) I\ (+, +) I (+,+), I I ( − , + ) II\ ( -, +) II (−,+), I I I ( − , − ) III (-, - ) III(−,−), I V ( + , − ) IV (+, - ) IV(+,−)。依照惯例,象限 I I I 的两个坐标都是正值;象限 I I II II 的 x-坐标是负值,y-坐标是正值;象限 I I I III III 的两个坐标都是负值的;象限 I V IV IV 的 x-坐标是正值,y-坐标是负值。所以象限的编号是按照逆时针方向,从象限 I I I 编到象限 I V IV IV。
2. 三维坐标系统
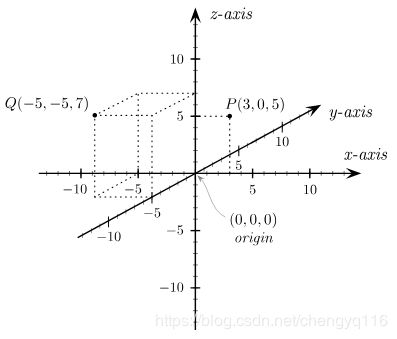
在原本的二维直角坐标系,再添加一个垂直于 x-轴,y-轴的坐标轴,称为z-轴。这三个坐标轴满足右手定则,则可得到三维的直角坐标系。z-轴与 x-轴,y-轴相互正交于原点。在三维空间的任何一点 P,可以用直角坐标 ( x , y , z ) (x, y, z) (x,y,z) 来表达其位置。参阅图 4,两个点 P 与 Q 的直角坐标分别为 ( 3 , 0 , 5 ) (3, 0, 5) (3,0,5) 与 ( − 5 , − 5 , 7 ) ( - 5, - 5, 7) (−5,−5,7)。
三个平面,xy-平面,yz-平面,xz-平面,将三维空间分成了八个部分,称为卦限 (octant)。与二维空间的四个象限不同,只有一个卦限有编号。第一号卦限的每一个点的三个坐标都是正值的。
3. 二维空间
直角坐标系的 x-轴与 y-轴必须相互垂直。包含 y-轴的直线为 y-线。在二维空间里,当我们设定了 x-轴的位置与方向的同时,我们也设定了 y-线的方向。可是,我们仍旧必须选择,在 y-线的以原点为共同点的两条半线中,哪一条半线的点的坐标是正值的,哪一条是负值的?任何一种选择决定了 xy-平面的取向。
图 1 中正值的 x-轴横地指向右方,正值的 y-轴纵地指向上方。这种取向称为正值取向、标准取向或右手取向。
右手定则是一种常用的记忆方法,专门用来辨认正值取向:将一只半握拳的右手放在平面上,大拇指往上指,其它的手指都从x-轴指向y-轴。
采用左手定则专门用来辨认负值取向或左手取向:将一只半握拳的左手放在 xy-平面上,大拇指往上指,其它的手指都从y-轴指向x-轴。
不论坐标轴是何种取向,将坐标系统做任何角度的旋转,取向仍旧会保持不变。
4. 三维空间
直角坐标系的 x-轴、y-轴与 z-轴必须相互垂直。包含 z-轴的直线为 z-线。在三维空间里,当我们设定了 x-轴、y-轴的位置与方向的同时,我们也设定了 z-线的方向。可是,我们仍旧必须选择,在 z-线以原点为共同点的两条半线中,哪一条半线的点的坐标是正值的,哪一条是负值的?这两种不同的坐标系统,称为右手坐标系与左手坐标系。右手坐标系又称为标准坐标系或正值坐标系。
右手坐标系这名词是由右手定则而来的。先将右手的手掌与手指伸直,然后将中指指向往手掌的掌面半空间,与食指呈直角关系。再将大拇指往上指去,与中指、食指都呈直角关系。则大拇指、食指与中指分别表示了右手坐标系的 x-轴、y-轴与 z-轴。同样地,用左手也可以表示出左手坐标系。
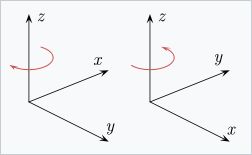
图 5 试着展示出一个左手坐标系与一个右手坐标系。用二维画面来展示三维物体,会造成扭曲或模棱两可的图形。指向下方与右方的轴,也有指向读者的意思;而位置居于中间的轴,也有指向读者正在看的方向的意思。平行于 xy-平面的红色圆形曲箭,其红色箭头从 z-轴前面经过,表示从 x-轴往 y-轴的旋转方向。