Lingo学习笔记（1）基本界面与解方程

一、Lingo基本界面

Step 1 ：打开Lingo。

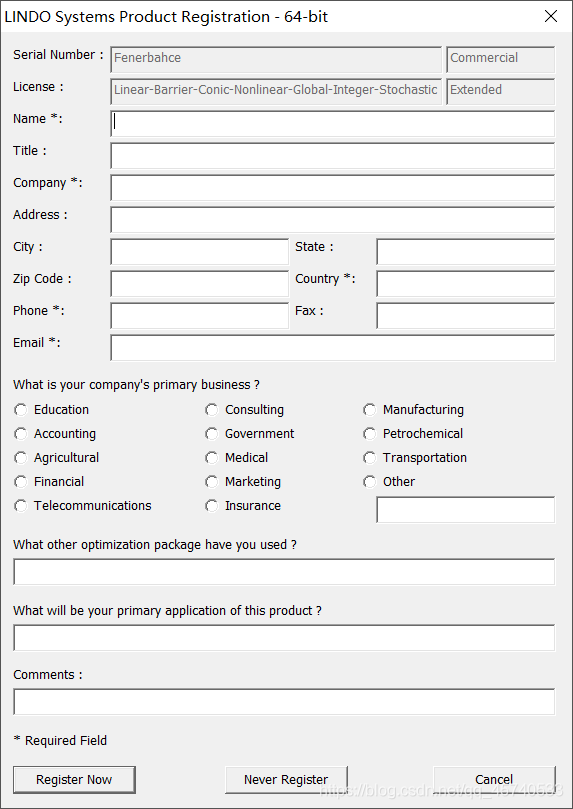
Step 2 : 弹出一个对话框，点击Cancel左边Never Register即可，其余内容用不到。

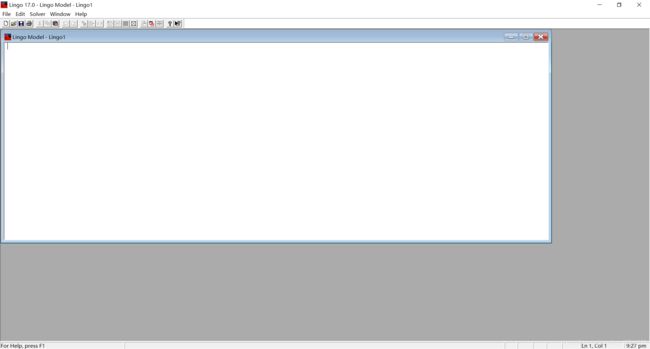
Step 3 ： 界面自动弹出名为“Lingo Model—Lingo 1 ”的窗口，用于书写代码。

Step 4 ：以解方程的题目：x+1=2为例，写完代码后，点击“红色的靶心”运行程序。

Step 5 ：首先Lingo会弹出一个名为“Solver Status”的对话框，它会显示运行时间。

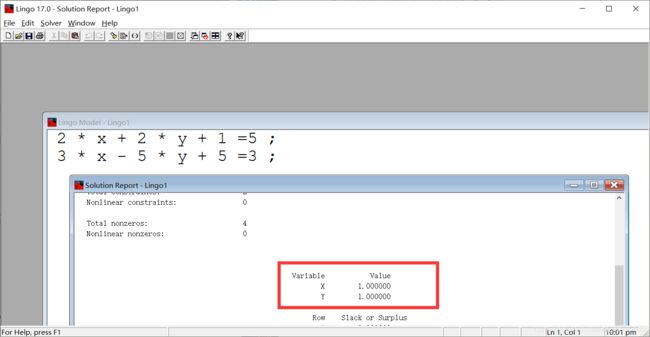
Step 6：然后，弹出一个名为“Solution Report”的界面。

Step 7：由此可知变量x的数值为1.

Step 8：如果是求解线性规划的话，目标值也会在“Solution Repoet”中给出。

二、用Lingo解方程

① 每个方程必须以分号“;”结束。

② 请注意：Lingo的所有符号都是英文格式下的符号。

③ Lingo的加减乘除分别是：+、-、*、/。

特别注意：

（1）2*x+1=1在Lingo中不可以简写为2x+1=1，乘号不能省略。

（2）注意除号“/”的形状，如同函数y=x的图像，而不是y = -x。

例题：求解方程组：
$$\{\begin{array}{l}2x+2y+1=5\\ 3x-5y+5=3\end{array}$$

解：

2 * x + 2 * y + 1 =5 ;
3 * x - 5 * y + 5 =3 ;

易错点：

① 不写结尾的分号。

② 不写乘号。

三、Lingo变量

① Lingo默认所有变量为大于0的数字，因而非负的条件不必多写。

② 万一遇到一个变量可以小于0，可以使用一个函数叫做@free，来使其定义域为R。

③ m和M等价，Lingo不区分大小写，所以mmm、mMm、MMM被视作同一个变量。所以，在Lingo的使用过程中，全程使用小写为宜。

④ 在变量命名方面还是尽量字母在前的命名方式。例如：x , x1 , max_x。

注意：在读取矩阵中的元素的时候，第一个元素是x(1)，不是x1。

例题：求解方程组：
$$\{\begin{array}{l}{x}^2+y^2+2x=103\\ 2x+y=12\\ x>0\\ y>5\end{array}$$
解

x^2 + y^2 + 2*x = 103;
        2*x + y = 12;
              x > 0;
              y > 5;

注意：

① 不要忘记分号。

② 不要忘记乘号。

③ 不要忘了x > 0 是Lingo默认条件，不用写。

四、线性规划基础

① 一个线性规划中只含一个目标函数。（两个以上是多目标线性规划，Lingo无法直接解）

② 求目标函数的最大值和最小值分别用max=。。。或min=。。。来表示。

③ 以!开头，以;结束的语句是注释语句。

④ 线性规划和非线性规划的本质区别是目标函数是否线性，其余一致，故不需要区分。但值得注意的是，非线性规划的求解十分困难，基本得不到区局最优解。

例：
某工厂有两条生产线，分别用来生产M 和P 两种型号的产品，利润分别为 200 元/个和 300 元/个，生产线的最大生产能力分别为每日 100 和 120，生产线每生产一个 M 产品需要1 个劳动日（1 个工人工作 8 小时称为1 个劳动日）进行调试、检测等工作，而每个 P 产品需要 2 个劳动日，该厂工人每天共计能提供 160 劳动日，假如原材料等其他条件不受限制，问应如何安排生产计划，才能使获得的利润最大？

$$\text{解：设两种产品的生产量分别为 设两种产品的生产量分别为}{x}_1\text{和}{x}_2\text{则该问题的数学模型为:}$$
目标函数：
$$\max z=200x_1+300x_2$$

约束条件为：
$$\{\begin{array}{l}{x}_1\le 100\\ x_2\le 120\\ x_1+2x_2\le 160\\ x_i\ge 0,i=1,2\end{array}$$
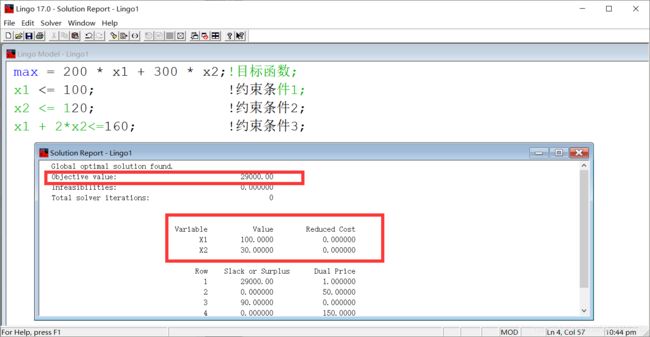
程序：

max = 200 * x1 + 300 * x2;!目标函数;
x1 <= 100;                !约束条件1;
x2 <= 120;                !约束条件2;
x1 + 2*x2<=160;           !约束条件3;