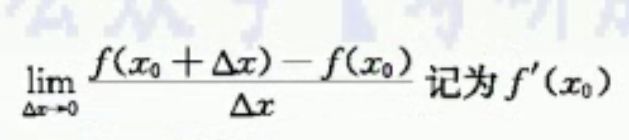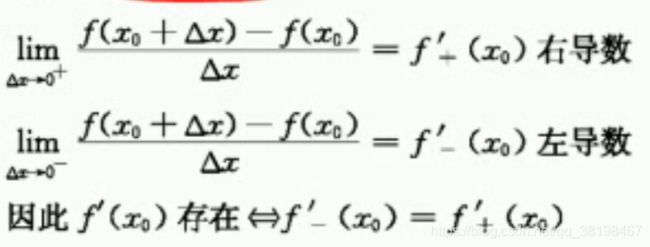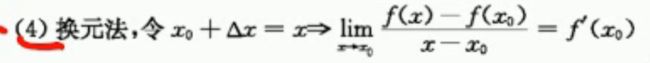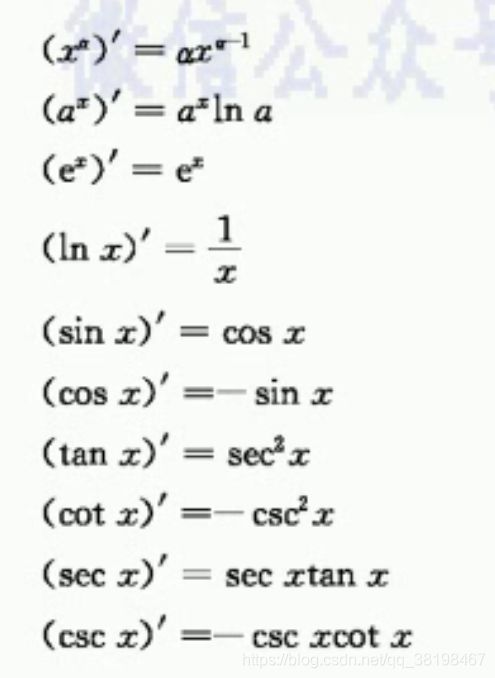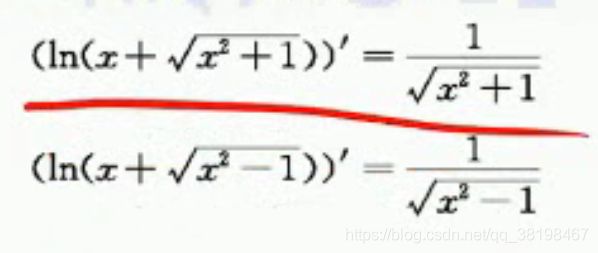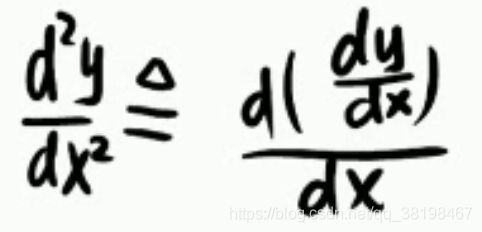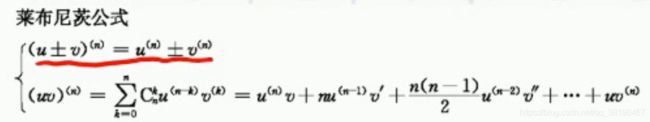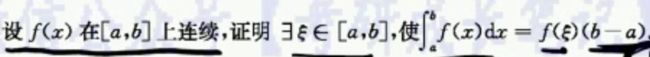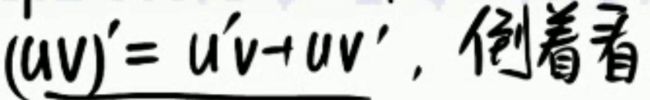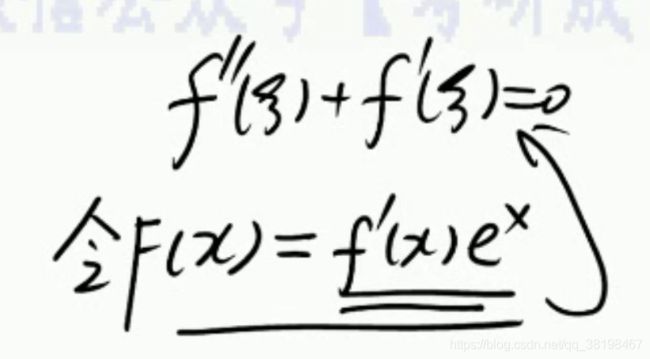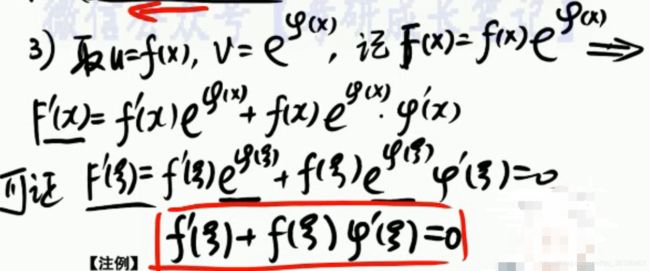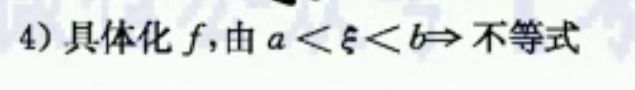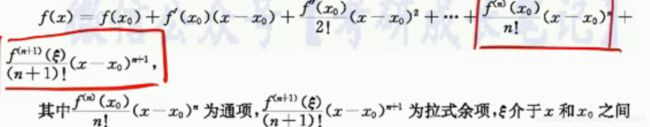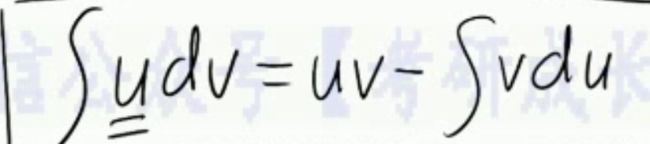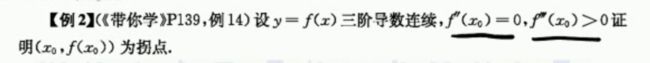高等数学：一元函数微分学

导数的定义：

当变化量趋近于零的时候，函数值的差和自变量的差的比值，就是导数的定义，我们也叫瞬时变化率，也叫变化率。

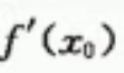实际上我们也会使用这个样子的形式来表示导数，它和表示的是同一个东西。前面那个是导数，后面这个也是导数。

导数的精华

因为这样的定义和我们说的极限其实就是一个道理了，所以需要注意到这些细节

1.左右有别

没错，就是这个样子，一定要注意到，一个点的导数如果存在，那么也是它的左右都存在且相等才行。我们拿上面的变化量来说，如果是0+，那么很明显是加上了一个正的无穷小量，说明就是下一时刻的东西，下一瞬间！反之如果是负无穷小量，那么表明的肯定就是上一时刻的事情了。

2.导数的等价写法：

 ：

很明显，我们换元之后，当趋近于0的时候，那x就趋近于x0了，这样我们的式子就可以改写成后面这个式子，实际上和上面的定义是一回事儿，但是不是不同的写法，这个也很重要，记下来。 

需要记住的小技巧：

1.凡是看到求一个点的导数，必定先把导数的定义公式拿出来，上面两个都是导数的定义公式。

2.对于这样的式子，我们可以看到，x的绝对值除以x，它的自变量范围只要是非零就行了，但是这个函数的函数值是始终只有两个的，要么是1，要么是-1，说明这个函数一定是一个有界函数呀。这是常见的，一定要记住。

无穷小量*有界量一定是无穷小量。

3.导数公式的广义化：

这个依靠们自己的思维去凑这样的一个广义化公式。

小技巧：

1.一般我们碰到抽象的式子，使用增量式的定义公式，如果是具体的函数表达式，那么我们使用差值式来解决

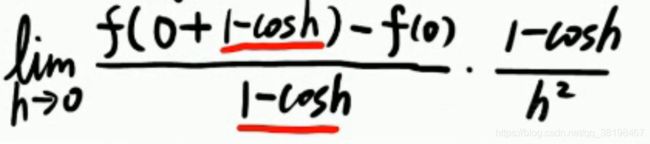
2.0虽然在数量上表示不了什么，但是！！！请千万注意，它在我们使用导数定义公式的时候有极大的作用，因为有的时候你减去一个0大小没有发生变化，但是它却凑出了在0这一点的导数定义公式，就像下面这样。

这个是增量式的导数定义公式。这个式子中，f(0)的函数值为0，但是我们一定要这样写，因为这样一写出来，我们是否就明确的发现，它满足导数的定义公式了？

3.cosx和sinx这种函数是一种天生的单侧极限函数，比如在正数这边，他们是一定不能超过1的，如果趋近于1，那一定就是1的左极限。明白把。所有有些题目一定要注意这一点。

4.一静一动原则：

一静一动原则就是前面那个是可以动的，但是后面减去的这个东西是不能动的，反正只要看见前面后面都在动的就是错的。违反了导数的基本原则。

小技巧:

1.千万要注意一点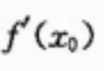，这个是一个记号，表示的是x0这个点的导数，如果它存在，那么它是一个具体的数，但是他还有可能不存在的。我们理解清楚一点，导数确实是一个具体的数，但是前提条件是它要存在，如果它不存在的时候，他就啥也不是了。

2.，这里要注意，有界但是极限不一定存在的。但是极限如果存在，那么函数是必定有界的。

3.和，这两点，不用证明，记住直接使用。也就是说，一个可导函数，导完之后，奇偶性互换。

导数的计算：

基本求导公式：

6大求导方式：

复合函数求导：

一层一层的求导即可。

隐函数求导：

这里需要注意的是，隐函数中的y不是一个变量，而是一个函数，所以求导的时候要把他当成函数来求导。

3.对数求导法：

比如下面这个式子

我们就是对式子两边都取对数进行化简。

4.反函数求导：

反函数求导其实很简单，注意写法即可

同时呢！对于具体型的反函数的导数求解，我们可以先求函数的导数，然后再求函数导数的导数，为什么呢？

很明显，函数的导数和它的反函数的导数，互为倒数关系。

5.参数方程求导

求导的时候我们一定要清楚，到底是对谁求导。

注意的地方：

我们的二阶导数实际上可以写成这个样子。

在求导的过程中，我们始终记住一句话，这个式子是那个变量的函数，我们就对那个变量求导。

6.高阶导数：

使用莱布尼兹公式的时候为下面这两个公式

第一个没得说，和差的n阶导数，等于n阶导数的和差。

而第二个乘积的高阶导数那该怎么办呢？同样是按照我们的这个公式来，此消彼长，好好理解一下，但是呢，考研中不会让我们把所有的式子都列出来，一般是列出前面的三项，后面的肯定都是0了，不然这计算量不符合逻辑的。

另外对于高阶公式，我们还应该记住以下这些公式，在一些只有几项的高阶导数计算中需要用到。

中值定理：

十大定理：

第一系列定理：

做题套路： 

介值定理三部曲：

第二系列定理：

10.积分中值定理

罗尔定理的使用技巧：

罗尔定理：比区间内连续，开区间内可导！妙啊···

在使用罗尔定理时候的注意点，通常情况下，我们由罗尔定理的定义可以知道

端点值相同，推出一定存在一个数，使得这一点的导数等于0，那么在实际的题目中，他一定会这样出题

它会把这个函数变得复杂。这样增大计算量，但是核心的东西还是罗尔定理的那一套。

罗尔定理解题方法一：求导公式逆用法

求导公式的逆用法；我们看见的求导公式可能是这样的。

但是注意，使用罗尔定理的时候，求导公式这个工具，可以反过来看看。

注意技巧：一：

当我们想证明：

我们可以立马想到辅助公式：

这里把大F和上面的复杂化函数联系起来。

注意技巧：二：

注意我们这里都是对罗尔定理的广义化，因为实际上的题目是不会直接把这个函数弄的那么简单的，一定是下面这种，或者上面的形式。他是多变的，需要我们结合前面的知识

技巧三：

由上面三个技巧我们可以总结出来，用好罗尔定理，实际要明白那个函数到底怎么拼凑，也就是辅助函数怎么做，就像几何中的辅助线一样，那么上面是三种常见的辅助函数。加深理解，一定是没有问题的。

解题经验：

什么意思呢？就是说在证明题中，只要看到定积分，就先用积分中值定理处理一下再说。 

罗尔定理解题方法二：积分还原法：

第三步移项之后得到的F(x)就是辅助函数

拉格朗日中值定理的使用：

实际上，拉格朗日中值定理是罗尔定理的一般化。

第一种思路：将f复杂化

第二种思路：给出相对高阶的条件，证明低阶不等式

在中值定理的求解过程中，如果出现多个点，那么最好画图

第三种思路：给出相对低阶条件，证明高阶不等式

第四种思路：具体化

第五种思路：的具体化

柯西中值定理的应用：

泰勒公式的应用：

1.带拉格朗日余项的泰勒公式

但是不需过多的担心，我们记住这个通式和余项，一般来讲，考研是考到2阶，最多到3阶。 

麦克劳林公式，这个也是很重要的。

这是二阶展开式：

2.带佩亚诺余项的泰勒公式；

这个一般就是我们第一章计算极限的时候使用，这里就不再过多的讲解。

在证明题中使用泰格公式的解题信号：

注意点，定积分是一个数。

需要记住的一个积分公式： 

导数的几何应用：

这里可以见讲义； 

三点、两性、一线：极值点、最值点、拐点；单调性、凹凸性；渐近线

需要记住的结论：

这个可以直接用，就是说，一个函数的三阶导数连续，同时在一个点的二阶导数等于0，三阶导数>0。那么个点一定是拐点。