顺序表和链表的优缺点（区别、特点）详解

顺序表和链表由于存储结构上的差异，导致它们具有不同的特点，适用于不同的场景。本节就来分析它们的特点，让读者明白 " 在什么样的场景中使用哪种存储结构" 更能有效解决问题。

通过系统地学习顺序表和链表我们知道，虽然它们同属于线性表，但数据的存储结构有本质的不同：

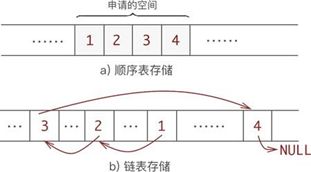
1. 顺序表存储数据，需预先申请一整块足够大的存储空间，然后将数据按照次序逐一存储，数据之间紧密贴合，不留一丝空隙，如图-1a 所示；
2. 链表的存储方式与顺序表截然相反，什么时候存储数据，什么时候才申请存储空间，数据之间的逻辑关系依靠每个数据元素携带的指针维持，如图-1b所示；

 

图 1 顺序表和链表的存储结构对比

基于不同的存储结构，顺序表和链表有以下几种不同。

开辟空间的方式

顺序表存储数据实行的是 "一次开辟，永久使用"，即存储数据之前先开辟好足够的存储空间，空间一旦开辟后期无法改变大小（使用动态数组的情况除外）。

而链表则不同，链表存储数据时一次只开辟存储一个节点的物理空间，如果后期需要还可以再申请。

因此，若只从开辟空间方式的角度去考虑，当存储数据的个数无法提前确定，又或是物理空间使用紧张以致无法一次性申请到足够大小的空间时，使用链表更有助于问题的解决。

空间利用率

从空间利用率的角度上看，顺序表的空间利用率显然要比链表高。

这是因为，链表在存储数据时，每次只申请一个节点的空间，且空间的位置是随机的，如图 2 所示：

 

图 2 链表结构易产生碎片

这种申请存储空间的方式会产生很多空间碎片，一定程序上造成了空间浪费。不仅如此，由于链表中每个数据元素都必须携带至少一个指针，因此，链表对所申请空间的利用率也没有顺序表高。

空间碎片，指的是某些容量很小（1KB 甚至更小）以致无法得到有效利用的物理空间。

时间复杂度

解决不同类型的问题，顺序表和链表对应的时间复杂度也不同。

根据顺序表和链表在存储结构上的差异，问题类型主要分为以下 2 类：

1.       问题中主要涉及元素的插入、删除和移动操作极少而遍历较多；

2.       问题中主要涉及元素的插入、删除和移动而访问元素的需求很少；

第 1 类问题适合使用顺序表。这是因为，顺序表中存储的元素可以使用数组下标直接访问，无需遍历整个表，因此使用顺序表访问元素的时间复杂度为O(1),链表访问元素的时间复杂度为O(n).

第 2 类问题则适合使用链表。链表中数据元素之间的逻辑关系靠的是节点之间的指针，当需要在链表中某处插入或删除节点时，只需改变相应节点的指针指向即可，无需大量移动元素，因此链表中插入、删除或移动数据所耗费的时间复杂度为O(1)；而顺序表中，插入、删除和移动数据可能会牵涉到大量元素的整体移动，因此时间复杂度至少为O(n).

综上所述，不同类型的场景，选择合适的存储结构会使解决问题效率成倍数地提高。