2020HDU多校第四场补题

题目链接

$3+4$ 一共七个题（6806没写出来我自闭了，关闭流同步后没注意遗留了一个$scanf$在里面，然后$debug$到自闭，赛后才发现。。太亏惹）
-----------------------------

签到题，首先我们想要赢肯定要拿能最短时间解决掉对手的武器，所以我们直接遍历一下找出时间最短的武器的个数$cnt$，之后就是分两种情况叠加

1. 对手没有拿最快的武器，那就直接获胜，为$(n-cnt)/n$，
2. 对手也拿了最快的武器，那就是胜率对半分，为$0.5\ast cnt/n$
   所以答案为$1-cnt/n\ast 0.5$

数据小，我直接利用$map$的内部自动排序找出的最快武器的数目

map<int, int> mp;
void Solve(int& kase) {
    int n;
    mp.clear();
    scanf("%d", &n);
    rep(i,1,n) {
        scanf("%d %d", &vec[i].fi, &vec[i].se);
        int Time = 100 % vec[i].fi == 0 ? 100 / vec[i].fi * vec[i].se - vec[i].se : 100 / vec[i].fi * vec[i].se;
        mp[Time] ++;
    }
    auto it = mp.begin();
    int cnt = it -> second;
    printf("%.7f\n", 1.0 - 0.5 * cnt / n);
}

题意简单，就是$01$背包裸题，找出两者重量相同时的最大价值就可以了
问题是数据量太大，会超时，所以这里用了个小技巧（黑科技）
随机算法…
首先我们处理成一个数组，把第二批都处理成负数，然后只需要求出$DP[0]$的贡献就可以了，这时候我们需要随机打乱原数组，之后约束一下范围，大小在范围外的直接忽略不计（出错概率很小…题解有证明，看不懂）
然后就可以了，由于有负数，所以整体加上一个$base$，最后判断$base$的贡献，（注意对于负数的背包处理方式）

const int maxn = 1e3 + 7;
const int base = 4e4 + 7;
const LL inf = -1e15;
LL DP[base << 1];
template<typename T>
T _max(const T& a, const T& b) {
    return a > b ? a : b;
}
int n, m, sum;
pair<int, int> arr[maxn << 1];
void solve () {
    fill(DP, DP + (base << 1), inf);
    // de(DP[base * 2 - 1])
    DP[base] = 0;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n + m; ++ i) {
        //de(DP[i])
        scanf("%d %d", &arr[i].first, &arr[i].second);
        if(i > n) {
            arr[i].first *= -1;
        }
    }
    random_shuffle(arr + 1, arr + n + m + 1);
    random_shuffle(arr + 1, arr + n + m + 1);
    for(int i = 1; i <= n + m; ++ i) {
        int w = arr[i].first;
        LL v = arr[i].second;
        if(w > 0) {
            for(int j = base * 2 - 1; j >= w; -- j) {
                if(DP[j - w] != inf) {
                    DP[j] = max(DP[j], DP[j - w] + v);
                    //de(DP[j])
                }
            }
        } else {
            for(int j = -w; j <= base * 2 - 1; ++ j) {
                if(DP[j] != inf) {
                   // de(j)
                    DP[j + w] = max(DP[j + w], DP[j] + v);
                    //de(DP[j + w])
                }
            }
        }
    }
    printf("%lld\n", DP[base]);
}

此题详见我这篇博客

·
·
·
·
·
·

题意简单，由于每个单词如果要交换的话，那就只能和它前面后面两个数交换，我们这里把一个数和它后面交换不进行处理，直接看做他后面的数和他前面交换就行
开一个数组$DP[n]$,每个位置$DP[i]$代表$i$和前面交换与不交换所能取得的最大价值，之后状态转移就是，如果这个单词和它前面一样，那就没有交换的意义，就直接等于$DP[i-1]$，如果和它前面单词不一样，那就加上交换与不交换的贡献，也就是$DP[i-1]+DP[i-2]$，所以就是

    DP[1] = 1;
    DP[2] = str[1] == str[2] ? 1 : 2;
    rep(i,3,n) {
        if(str[i] != str[i - 1]) {
            DP[i] = DP[i - 2] + DP[i - 1];
        } else {
            // if(str[i - 1] == str[i - 2]) {
                DP[i] = DP[i - 1];
            // } else {

            // }
        }
        DP[i] %= mod;
    }

全部代码是

string str[maxn];
int n;
LL DP[maxn];
void Solve(int& kase) {
    cin >> n;
    rep(i,1,n) {
        cin >> str[i];
    }
    if(n == 1) {
        cout << 1 << endl;
        return ;
    } else if(n == 2) {
        if(str[1] == str[2]) {
            cout << 1 << endl;
        } else {
            cout << 2 << endl;
        }
        return ;
    }
    DP[1] = 1;
    DP[2] = str[1] == str[2] ? 1 : 2;
    rep(i,3,n) {
        if(str[i] != str[i - 1]) {
            DP[i] = DP[i - 2] + DP[i - 1];
        } else {
            // if(str[i - 1] == str[i - 2]) {
                DP[i] = DP[i - 1];
            // } else {

            // }
        }
        DP[i] %= mod;
    }
    cout << DP[n] << endl;
}

同时学到个黑科技，可以这样搞

char str[1005]; scanf("%s",str);
string ptr = str;

可以用字符串给$string$类赋值，所以我再也不用$cin$了，太亏了，，，这个题没写出来，关闭流同步后还用$scanf$，我真是憨批+眼瞎没看到

最小点覆盖+HK算法
比赛的时候画图分线段连接正或负想到了二分匹配最小点覆盖，，但是觉得怪怪的就没写，我真的是憨批，好迷啊我。。。用$map$模拟了一下午。。
我们假设每个人要么是正着，要么是反着，延长线段或者与坐标轴的交点，交点能重合的就可以为同一个人，我们把坐标轴倾斜45度就是一个很常规的最小点覆盖了，，，根据一些奇奇怪怪的证明，最大匹配数等于最小点覆盖
下次一定想到就实现一下莽一发

vector<int> G[maxn], X, Y;
vector<pii> input;
int totx, toty, mx[maxn], my[maxn], dx[maxn], dy[maxn], dis;
bool used[maxn];
int getid(int x, const vector<int>& vec) {
    return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
}
bool BFS() {
    memset(dx, -1, sizeof(dx));
    memset(dy, -1, sizeof(dy));
    dis = inf;
    queue<int> Q;
    for(int i = 1; i <= totx; ++ i) {
        if(mx[i] == -1) {
            dx[i] = 0;
            Q.push(i);
        }
    }
    while(!Q.empty()) {
        int u = Q.front();
        Q.pop();
        if(dx[u] > dis) break;
        for(auto x : G[u]) {
            if(dy[x] == -1) {
                dy[x] = dx[u] + 1;
                if(my[x] == -1) {
                    dis = dy[x];
                } else {
                    dx[my[x]] = dy[x] + 1;
                    Q.push(my[x]);
                }
            }
        }
    }
    return dis != inf;
}
bool DFS(int u) {
    for(auto x : G[u]) {
        if(!used[x] && dy[x] == dx[u] + 1) {
            used[x] = true;
            if(my[x] != -1 && dy[x] == dis) {
                continue;
            }
            if(my[x] == -1 || DFS(my[x])) {
                mx[u] = x;
                my[x] = u;
                return true;
            }
        }
    }
    return false;
}
int MaxMatch() {
    memset(mx, -1, sizeof(mx));
    memset(my, -1, sizeof(my));
    int res = 0;
    while(BFS()) {
        memset(used, false, sizeof(used));
        for(int i = 1; i <= totx; ++ i) {
            if(mx[i] == -1 && DFS(i)) {
                ++ res;
            }
        }
    }
    return res;
}
void Solve() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i) {
        G[i].clear();
    }
    input.resize(n);
    X.clear(), Y.clear();
    for(int i = 0; i < n; ++ i) {
        scanf("%d %d", &input[i].first, &input[i].second);
        X.emplace_back(input[i].second - input[i].first);
        Y.emplace_back(input[i].second + input[i].first);
    }
    // unique
    sort(X.begin(), X.end());
    sort(Y.begin(), Y.end());
    X.resize(unique(X.begin(), X.end()) - X.begin());
    Y.resize(unique(Y.begin(), Y.end()) - Y.begin());
    totx = X.size(), toty = Y.size();

    for(int i = 0; i < n; ++ i) {
        int valx = input[i].second - input[i].first, valy = input[i].second + input[i].first;
        int posx = getid(valx, X), posy = getid(valy, Y);
        G[posx].emplace_back(posy);
    }
    printf("%d\n", MaxMatch());
}

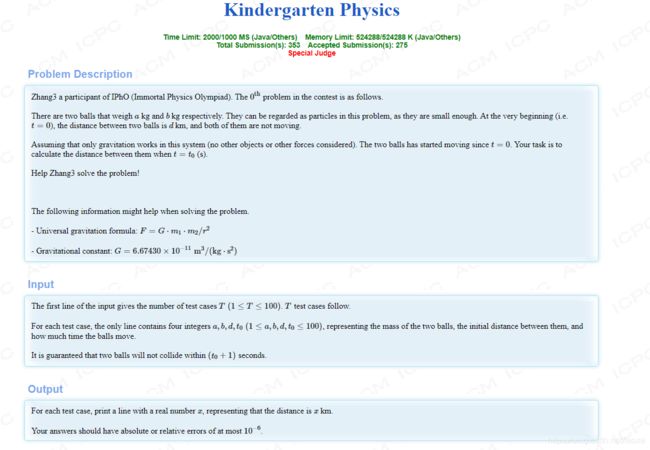
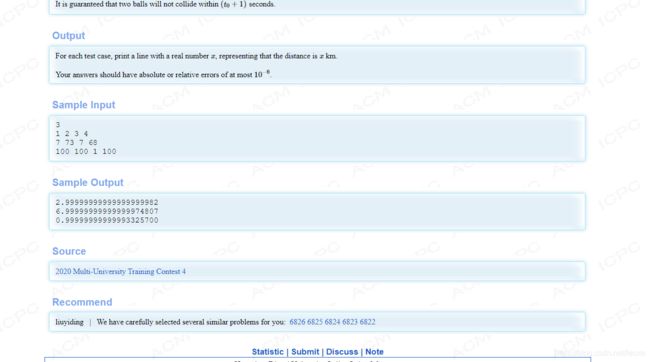
这个…毒瘤啊
比赛时我队数学选手不在，两个人打，另一个队友物理不好就丢给我了。。。wtm我一个高数2.0绩点的菜逼在这求积分把我求自闭了
绝望后看到了最后一个样例…数据跑满也只减小了0.00000000000000001…
我吐了，直接输出(x-1).99999999999就过了

void Solve(int& kase) {
    int a, b, c, d;
    cin >> a >> b >> c >> d;
    -- c;
    printf("%d.999999999999999\n",c);
}

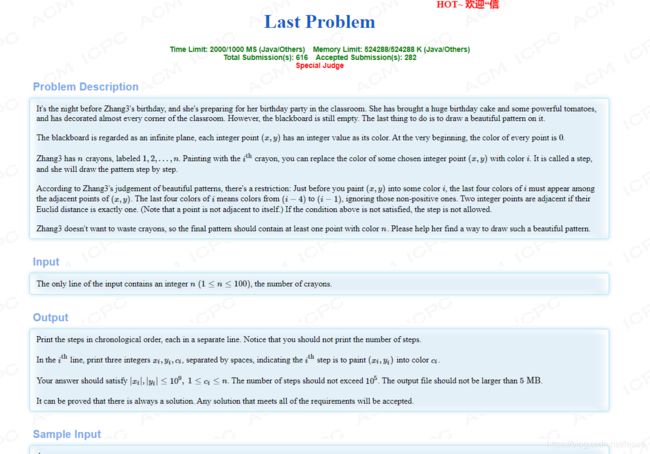
构造题，直接按照如下方式构造

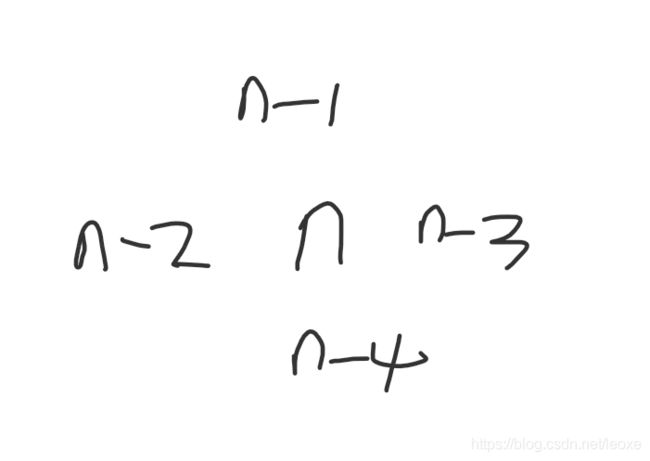
DFS一下，对于目前值小于等于0的直接返回就好

#include 
#include 
using namespace std;
int res[5005][5005];
void Solve(int x, int y, int val) {
    if (val <= 0)  return ;
    if(res[x][y - 1] != val - 1) {
        Solve(x, y - 1, val - 1);
    }
    if(res[x - 1][y] != val - 2) {
        Solve(x - 1, y, val - 2);
    }
    if(res[x][y + 1] != val - 4) {
        Solve(x, y + 1, val - 4);
    }
    if(res[x + 1][y] != val - 3) {
        Solve(x + 1, y, val - 3);
    }
    res[x][y] = val;
    printf("%d %d %d\n", x, y, val);
}
int main () {
    int n;
    scanf("%d", &n);
    memset(res, 0, sizeof(res));
    Solve(2500, 2500, n);
    return 0;
}