cf Educational Codeforces Round 55 D. Maximum Diameter Graph

原题：
D. Maximum Diameter Graph
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Graph constructive problems are back! This time the graph you are asked to build should match the following properties.

The graph is connected if and only if there exists a path between every pair of vertices.

The diameter (aka “longest shortest path”) of a connected undirected graph is the maximum number of edges in the shortest path between any pair of its vertices.

The degree of a vertex is the number of edges incident to it.

Given a sequence of n integers a1,a2,…,an construct a connected undirected graph of n vertices such that:

the graph contains no self-loops and no multiple edges;
the degree di of the i-th vertex doesn’t exceed ai (i.e. di≤ai);
the diameter of the graph is maximum possible.
Output the resulting graph or report that no solution exists.

Input
The first line contains a single integer n (3≤n≤500) — the number of vertices in the graph.

The second line contains n integers a1,a2,…,an (1≤ai≤n−1) — the upper limits to vertex degrees.

Output
Print “NO” if no graph can be constructed under the given conditions.

Otherwise print “YES” and the diameter of the resulting graph in the first line.

The second line should contain a single integer m — the number of edges in the resulting graph.

The i-th of the next m lines should contain two integers vi,ui (1≤vi,ui≤n, vi≠ui) — the description of the i-th edge. The graph should contain no multiple edges — for each pair (x,y) you output, you should output no more pairs (x,y) or (y,x).

Examples
input
3
2 2 2
output
YES 2
2
1 2
2 3
input
5
1 4 1 1 1
output
YES 2
4
1 2
3 2
4 2
5 2
input
3
1 1 1
output
NO
Note
Here are the graphs for the first two example cases. Both have diameter of 2.

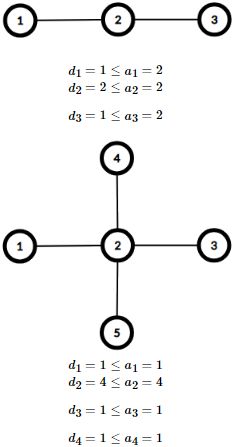
中文：

给你n个节点，每个节点i要求度值不能超过$a_i$，现在让你构造一个无向连通图。使得这个连通图的直接最长，
联通图的直接就是任意两个节点之间的最短路径当中最长的那条路径长度值。

代码：

#include
using namespace std;

typedef long long ll;
const int maxn=501;
typedef pair<int,int> pii;
struct node
{
    int cnt,ind;//度和下标
};

deque<int> a;
int n,mark[maxn];
int ans;
int g[maxn][maxn];
node b[maxn];
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>n)
    {
        int big=0,two=0,one=0;
        int flag=0,res=0;
        a.clear();

        for(int i=1;i<=n;i++)
        {
            cin>>res;
            a.push_back(res);
            b[i].cnt=res;
            b[i].ind=i;
            if(res>2)
                big++;
            if(res==2)
                two++;
            if(res==1)
                one++;
        }
        memset(mark,0,sizeof(mark));
        ans=0;
        memset(g,0,sizeof(g));

        sort(a.begin(),a.end(),greater<int>());
        priority_queue<int> pq;

        pq.push(a.front());
        a.pop_front();
        while(true)
        {
            if(pq.empty())
            {
                if(!a.empty())
                    flag=1;
                break;
            }
            if(a.empty())
                break;
            int t=pq.top();
            pq.pop();
            for(int i=0;i<t&&i<a.size();i++)
            {
                a[i]--;
                if(a[i])
                    pq.push(a[i]);
            }
            while(t&&!a.empty())
            {
                a.pop_front();
                t--;
            }
        }
        if(flag)
        {
            cout<<"NO"<<endl;
            continue;
        }
        ans=big+two-1;
        if(one>=2)
            ans+=2;
        if(one==1)
            ans+=1;
        cout<<"YES"<<" "<<ans<<endl;
        sort(b+1,b+1+n,[](node& n1,node& n2){return n1.cnt>n2.cnt;});
        res=0;


        for(int i=1;i<n;i++)
        {
            if(b[i].cnt>0&&b[i+1].cnt>0)
            {
                b[i+1].cnt--;
                b[i].cnt--;
                g[b[i+1].ind][b[i].ind]=g[b[i].ind][b[i+1].ind]=1;
                res++;
            }
            else
            {
                if(b[i].cnt==0)
                {
                    for(int j=1;j<i;j++)
                    {
                        if(b[j].cnt>0)
                        {
                            b[j].cnt--;
                            b[i+1].cnt--;
                            g[b[i+1].ind][b[j].ind]=g[b[j].ind][b[i+1].ind]=1;
                            res++;
                            break;
                        }
                    }
                }
            }
        }
        cout<<res<<endl;
        for(int i=1;i<=n;i++)
        {
            for(int j=i+1;j<=n;j++)
            {
                if(g[i][j])
                    cout<<i<<" "<<j<<endl;
            }
        }

    }
	return 0;
}

思路：

此题挺简单的，首先判断能不能构成一个连通图。先将图的度从大到小排序，依次枚举当前的度值$d_i$，判断第i个节点后面有几个节点，如果有超过$d_i$个节点，那么将节点i后面$d_i$个节点连接到节点i上，同时将后面的$d_i$个节点的度值减去1，表示这些节点已经连接到节点i上，后面的节点同样操作。如果后面的节点数小于$d_i$则表示节点i可以将所有后面的节点连接完，即可构成一个连通图。

在构造好连通图后，考虑怎么样才能使得所有节点直接的最短路径中最长的那条尽量长呢？

很简单，尽量往长连接节点呗！

按照度值从大到小一次连接，如果发现最后一个节点的度值为0，不能继续连接了，那么就连接到开头，此时得到的就是最长的最短路径了（开头到结尾的长度），剩下的节点随便连接，对长度没有影响。

那么得到的最长路径的长度可以按照如下计算：
设one是度为1的节点个数，big是度大于等于2的节点个数。

如果one的值大于1，那么结果就是big+2-1（所有节点练成一串，度为1的节点放在两头，其余的随便连）
如果one的值小于等于1，那么就连接在结尾即可。

最后将连接好的图构造成图即可。