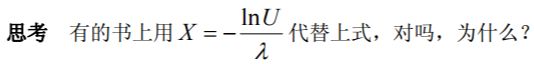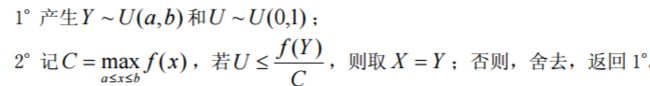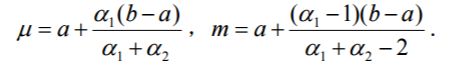排队论模型（八）：Matlab 生成随机数、排队模型的计算机模拟

---

排队论模型（一）：基本概念、输入过程与服务时间的常用概率分布

排队论模型（二）：生灭过程 、 M / M /s 等待制排队模型、多服务台模型

排队论模型（三）：M / M / s/ s 损失制排队模型

排队论模型（四）：M / M / s 混合制排队模型

排队论模型（五）： 有限源排队模型、服务率或到达率依赖状态的排队模型

排队论模型（六）：非生灭过程排队模型、爱尔朗（Erlang）排队模型

排队论模型（七）：排队系统的优化

排队论模型（八）：Matlab 生成随机数、排队模型的计算机模拟

---

目录

1 产生给定分布的随机数的方法

(i)反变换法

（ii）卷积法

(iii)取舍法

2 排队模型的计算机模拟

2.1 确定随机变量概率分布的常用方法

 2 .2  计算机模拟

---

1 产生给定分布的随机数的方法

Matlab 可以产生常用分布的随机数。下面我们介绍按照给定的概率分布产生随机数的一般方法，这些方法都以U(0,1) 分布的随机变量为基础。

(i)反变换法

定理 设 X 是一个具有连续分布函数 F(x) 的随机变量，则 F(X ) 在 [0，1] 上服 从均匀分布。

（ii）卷积法

(iii)取舍法

若随机变量 X 在有限区间(a,b) 内变化，但概率密度 f (x)具有任意形式（甚至没 有解析表达式），无法用前面的方法产生时，可用取舍法。一种比较简单的取舍法的步 骤是：

2 排队模型的计算机模拟

2.1 确定随机变量概率分布的常用方法

在模拟一个带有随机因素的实际系统时，究竟用什么样的概率分布描述问题中的随 机变量，是我们总是要碰到的一个问题，下面简单介绍确定分布的常用方法：

【1 】根据一般知识和经验，可以假定其概率分布的形式，如顾客到达间隔服从指数 分布 Exp(λ) ；产品需求量服从正态分布   ；订票后但未能按时前往机场登机 的人数服从二项分布 B(n, p) 。然后由实际数据估计分布的参数 λ,μ,σ 等，参数估计 可用极大似然估计、矩估计等方法。

【2】 直接由大量的实际数据作直方图，得到经验分布，再通过假设检验，拟合分布 函数，可用  检验等方法。 3 o 既缺少先验知识，又缺少数据时，对区间(a,b) 内变化的随机变量，可选用 Beta 分布（包括均匀分布）。先根据经验确定随机变量的均值 μ 和频率最高时的数值（即密度函数的最大值点）m ，则 Beta 分布中的参数   可由以下关系求出：

 2 .2  计算机模拟

当排队系统的到达间隔时间和服务时间的概率分布很复杂时，或不能用公式给出 时，那么就不能用解析法求解。这就需用随机模拟法求解，现举例说明。

例 14 设某仓库前有一卸货场，货车一般是夜间到达，白天卸货，每天只能卸货 2 车，若一天内到达数超过 2 车，那么就推迟到次日卸货。根据表 3 所示的数据，货车到 达数的概率分布（相对频率）平均为 1.5 车/天，求每天推迟卸货的平均车数。

解 这是单服务台的排队系统，可验证到达车数不服从泊松分布，服务时间也不服 从指数分布（这是定长服务时间）。 随机模拟法首先要求事件能按历史的概率分布规律出现。模拟时产生的随机数与事 件的对应关系如表 4。

我们用 a1 表示产生的随机数，a2 表示到达的车数，a3 表示需要卸货车数，a4 表 示实际卸货车数，a5 表示推迟卸货车数。编写程序如下：

clear
rand('state',sum(100*clock));
n=50000;
m=2
a1=rand(n,1);
a2=a1; %a2初始化
a2(find(a1<0.23))=0;
a2(find(0.23<=a1&a1<0.53))=1;
a2(find(0.53<=a1&a1<0.83))=2;
a2(find(0.83<=a1&a1<0.93),1)=3;
a2(find(0.93<=a1&a1<0.98),1)=4;
a2(find(a1>=0.98))=5;
a3=zeros(n,1);a4=zeros(n,1);a5=zeros(n,1); %a2初始化
a3(1)=a2(1);
if a3(1)<=m
    a4(1)=a3(1);a5(1)=0;
else
     a4(1)=m;a5(1)=a2(1)-m;
end
for i=2:n
    a3(i)=a2(i)+a5(i-1);
    if a3(i)<=m
        a4(i)=a3(i);a5(i)=0;
    else
        a4(i)=m;a5(i)=a3(i)-m;
    end
end
a=[a1,a2,a3,a4,a5];
sum(a)/n 

例 15 银行计划安置自动取款机，已知 A 型机的价格是 B 型机的 2 倍，而 A 型机 的性能—平均服务率也是 B 型机的 2 倍，问应该购置 1 台 A 型机还是 2 台 B 型机。 为了通过模拟回答这类问题，作如下具体假设，顾客平均每分钟到达 1 位， A 型 机的平均服务时间为 0.9 分钟， B 型机为 1.8 分钟，顾客到达间隔和服务时间都服从 指数分布，2 台 B 型机采取 M / M / 2 模型（排一队），用前 100 名顾客（第 1 位顾客到 达时取款机前为空）的平均等待时间为指标，对 A 型机和 B 型机分别作 1000 次模拟， 进行比较。

在模拟 A 型机时，我们用cspan表示到达间隔时间，sspan表示服务时间，ctime 表示到达时间，gtime表示离开时间，wtime表示等待时间。我们总共模拟了m 次， 每次n 个顾客。程序如下：

tic
rand('state',sum(100*clock));
n=100;m=1000;mu1=1;mu2=0.9;
for j=1:m
    cspan=exprnd(mu1,1,n);sspan=exprnd(mu2,1,n);
    ctime(1)=cspan(1);
    gtime(1)=ctime(1)+sspan(1);
    wtime(1)=0;
    for i=2:n
        ctime(i)=ctime(i-1)+cspan(i);
        gtime(i)=max(ctime(i),gtime(i-1))+sspan(i);
        wtime(i)=max(0,gtime(i-1)-ctime(i));
    end
    result1(j)=sum(wtime)/n;
end
result_1=sum(result1)/m 
toc

类似地，模拟 B 型机的程序如下：

tic
rand('state',sum(100*clock));
n=100;m=1000;mu1=1;mu2=1.8;
for j=1:m
    cspan=exprnd(mu1,1,n);sspan=exprnd(mu2,1,n);
    ctime(1)=cspan(1);ctime(2)=ctime(1)+cspan(2);
    gtime(1:2)=ctime(1:2)+sspan(1:2);
    wtime(1:2)=0;flag=gtime(1:2);
    for i=3:n
        ctime(i)=ctime(i-1)+cspan(i);
        gtime(i)=max(ctime(i),min(flag))+sspan(i);
        wtime(i)=max(0,min(flag)-ctime(i));
        flag=[max(flag),gtime(i)];
    end
    result2(j)=sum(wtime)/n;
end
result_2=sum(result2)/m
toc 

读者可以用下面的程序与上面的程序比较了解编程的效率问题。

tic
clear
rand('state',sum(100*clock));
n=100;m=1000;mu1=1;mu2=0.9;
for j=1:m
    ctime(1)=exprnd(mu1);
    gtime(1)=ctime(1)+exprnd(mu2);
    wtime(1)=0;
    for i=2:n
        ctime(i)=ctime(i-1)+exprnd(mu1);
        gtime(i)=max(ctime(i),gtime(i-1))+exprnd(mu2);
        wtime(i)=max(0,gtime(i-1)-ctime(i));
    end
    result(j)=sum(wtime)/n;
end
result=sum(result)/m
toc

---

1. 一个车间内有10台相同的机器，每台机器运行时每小时能创造4元的利润，且平 均每小时损坏一次。而一个修理工修复一台机器平均需4小时。以上时间均服从指数分 布。设一名修理工一小时工资为6元，试求：

（i）该车间应设多少名修理工，使总费用为最小；

（ii）若要求不能运转的机器的期望数小于4台，则应设多少名修理工；

（iii）若要求损坏机器等待修理的时间少于4小时，又应设多少名修理工。

2. 到达某铁路售票处顾客分两类：一类买南方线路票，到达率为λ1 /小时，另一 类买北方线路票，到达率为λ2 /小时，以上均服从泊松分布。该售票处设两个窗口，各窗口服务一名顾客时间均服从参数 μ = 10 的指数分布。试比较下列情况时顾客分别等 待时间Wq ：

（i）两个窗口分别售南方票和北方票；

（ii）每个窗口两种票均出售。（分别比较 λ1 = λ2 = 2,4,6,8 时的情形）

3. 一名修理工负责5台机器的维修，每台机器平均每2h损坏一次，又修理工修复一 台机器平均需时18.75min，以上时间均服从负指数分布。试求：

（1）所有机器均正常运转的概率；

（2）等待维修的机器的期望数；

（3）假如希望做到有一半时间所有机器都正常运转，则该修理工最多看管多少台 机器。

（4）假如维修工工资为8元/h，机器不能正常运转时的损失为40元/h，则该修理工 看管多少台机器较为经济合理。

---

排队论模型（一）：基本概念、输入过程与服务时间的常用概率分布

排队论模型（二）：生灭过程 、 M / M /s 等待制排队模型、多服务台模型

排队论模型（三）：M / M / s/ s 损失制排队模型

排队论模型（四）：M / M / s 混合制排队模型

排队论模型（五）： 有限源排队模型、服务率或到达率依赖状态的排队模型

排队论模型（六）：非生灭过程排队模型、爱尔朗（Erlang）排队模型

排队论模型（七）：排队系统的优化

排队论模型（八）：Matlab 生成随机数、排队模型的计算机模拟

---