图论学习笔记——最短路径之Dijkstra算法
Dijkstra（迪杰斯特拉）算法
Dijkstra算法是一种时间复杂度为
的算法，相较于时间复杂度为
的Floyd算法来说效率更高了一些，但是Dijkstra算法是一种单源路径算法，也就是说只能计算起点只有一个的情况，并且不能处理存在边的权值为负数的情况。
Dijkstra算法的实现（使用邻接矩阵储存图）
首先我们要定义一个一维的dis数组，设起点为s，则设dis[v]表示的是从起点s到点v的最短路径长度，如果题目要求输出具体路径，可以再申明一个pre数组，设pre[v]表示从起点走到点v的路径上点v的前一个节点（即点v的前驱节点），最后我们还需要建立一个bool类型的数组vis用来表示某一个点已经确定了距离起点s的最小距离。
在算法开始之前我们首先还要对数据进行初始化：dis[v]=
(v
s); dis[s]=0; pre[s]=0; vis[s]=true;
Dijkstra算法的基本思想是，从起点到一个点的最短路径至少要经过一个”中转点“，为了方便理解，我们把起点当做是距离起点为0的中转点（有点像在说绕口令。。。）。显然，我们要想求出起点到一个点的最短路径，那我们必然要先求出它的前一个中转点距离起点的最短路径。而要求出前一个中转点距离起点的最短路径必然就要求出前一个中转点的前一个中转点距离起点的最短路径······依此类推就可以一直递归到起点。
而我们要做的就是把这个过程反过来进行递推，从起点开始将起点到起点的距离标记为0（这是显而易见的），然后进行n次循环，每一次循环找到一个目前vis[A]==false且dis[A]最小的点A确定当前的dis[A]为最优解，即vis[A]=true;（根据下文的贪心策略可证得这样的操作是正确的）。接着枚举与A相接的点B，比较dis[B]与dis[A]+w[A][B]（也就是路径AB的距离），得到当前情况下点B到起点s的最短路径。
即如果dis[A]+w[A][B] < dis[B]，那么相对于点B来说更优的前驱节点为A，所以dis[B]=dis[A]+w[A][B]; pre[B]=A;
根据简单的数学原理可以非常容易的得出在循环结束后，dis和pre为最优解。
注：为了稍微提高一些程序的运行效率，我们一般手动进行第一次循环（当A=s时的情况）
即把所有与起点s相邻的点B的dis[B]设为w[s][B]，这样做之后我们就只用进行n-1次循环了。
代码实现如下（可根据题意自行舍弃pre数组）：
void Dijkstra(int s)
{
memset(dis,0x1f,sizeof(dis));
memset(vis,false,sizeof(pre));
dis[s]=0;
pre[s]=0;
vis[s]=true;
int i, j, k, min, max=dis[0];//initialize data
for(i=1; i<=n; ++i) dis[i]=w[s][i];//do the frist time
for(i=1; iDijkstra算法优化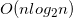
注：本节内容为进阶内容，需要自行学习了解，堆，优先队列，优先队列stl模板，std::pair等知识点。
你以为本文就这样结束了？不可能的（手动滑稽）。
我们知道，每一次循环的时候我们都需要在此循环中再进行一次循环用于寻找dis数组的最小值，这就需要浪费很多的时间。
我相信看到这里的人都学过或者是乖乖的去看了堆，优先队列的内容。试想一下，如果我们把dis数组扔到优先队列中。。。
咳，相信大家都已经明白我们要干什么了（手动滑稽），废话不多说，上代码（注：在将一对pair放入优先队列中时，优先队列会优先根据pair中的前一个对象进行排列，如果前一个对象相等，再考虑后一个对象，所以一定要把距离原点的距离放在前一个对象）：
#include
using namespace std;
void Dijkstra(int s)
{
typedef pair arr;
priority_queue,greater > pue;
memset(dis,0x1f,sizeof(dis));
memset(pre,0,sizeof(pre));
memset(vis,false,sizeof(vis));
dis[s]=0;
pre[s]=0;
pue.push(arr(0,s));//initialize data
while(!pue.empty())
{
int k=pue.top().second;
pue.pop();
if(vis[k]) continue;
vis[k]=true;
for(int j=1; j<=n; ++j)//updata dis and pre
{
if(dis[k]+w[k][j]