容斥原理——经典例题（组合数学）
一.容斥原理
就是人们为了不重复计算重叠部分，想出的一种不重复计算的方法。
先来认识一下这两个符号：
与
（如图）
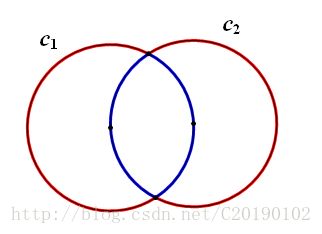
蓝色的圈就是c1c2，红色的圈围起来的就是c1c2
二.例题：组合数学
1.题目
1.1.题目描述
八是个很有趣的数字啊。八=发，八八=爸爸，88=拜拜。当然最有趣的还是8用二进制表示是1000。怎么样，有趣吧。当然题目和这些都没有关系。 某个人很无聊，他想找出[a,b]中能被8整除却不能被其他一些数整除的数。
1.2.输入
第一行一个数n，代表不能被整除的数的个数。 第二行n个数，中间用空格隔开。 第三行两个数a，b，中间一个空格。 a < =b < =1000000000
1.3.输出
一个整数，为[a,b]间能被8整除却不能被那n个数整除的数的个数。
1.4.样例输入
3
7764 6082 462
2166 53442
1.5.样例输出
6378
1.6.提示
对于30%的数据， 1 ≤n ≤5，1 ≤a ≤ b ≤ 100000。
对于100%的数据，1 ≤ n ≤15，1 ≤ a ≤ b ≤ 10^9，N个数全都小于等于10000大于等于1。
2.思路
这道题一看就是用容斥原理做吧，如果我们用ans表示答案，用B表示a到b的范围内可以被8整除的所有数，用E表示a到b范围内的所有数，Ai表示那n个要求不能整除的数，可以想到公式：
它的意义就是：所有范围内的数减去所有能被那n个数整除的数与所有范围内能被8整除的数的并集。
好，那么我们现在的问题就是如何求这些并集。（注意求两个数的并集就是求两个数的最小公倍数）
先举一个例子：假如有两个要求不被整除的数（如图，那两个数分别为1号圈和2号圈）：
那么，
也就是：ans=8-①-②+②-②-③
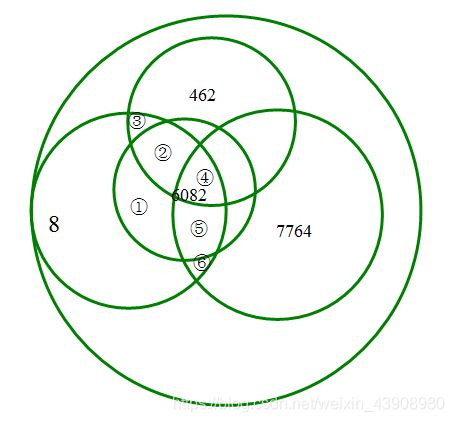
再来一个稍复杂的：
继续像例子1这样推：
说人话，就是：ans=8-（①+⑤+④+②）+（②+④）-（④）+（④+⑤） -（③+②+④）+（④） -（④+⑤+⑥）
可化简为：ans=8-①-②-④-③-⑤-⑥，就是我们想要求的答案了。大家可以发现，我打了下划线的部分是各个完整的部分，分别是8与其他数分别第一次并集
然后8与这个数并集之后，又依次与其他的数继续并集，并且不重不漏，还有，在一个完整的部分里第奇数次并集相减，第偶数次相加，如：ans=8-（①+⑤+④+②）+（②+④）-（④）+（④+⑤） -（③+②+④）+（④） -（④+⑤+⑥）
从8的集合开始，第0次加上8的集合内的所有数，到
开始第1次-（①+⑤+④+②）相减，第2次（②+④）相加，然后发现不能再并下去了，又回到，开始新的第1次-（④），第2次（④+⑤），发现也不能再走下去了，就到了
，继续走下去就走完了。所以，这就是一个递归进行的过程，一个深搜就完事了。
void dfs (int k, int Index, LL v){//k代表第几次并集，Index代表到了第几个集合，v代表这个集合，如v=8，就代表8的倍数这个集合
if (v > b)//超出范围就没有意义
return ;
if (k % 2 == 0)//第偶数次加，第基数次减
ans += b / v - a / v;
else
ans -= b / v - a / v;
for (int i = Index + 1; i <= n; i ++){
LL t = lcm (v, m[i]);//求着两个集合的并集
dfs (k + 1, i, t);//递归求解
}
}3.代码
#include
#include
#include
using namespace std;
#define LL long long
int n, m[130], a, b;
LL ans;
LL gcd (LL a, LL b){//最大公因数
if (! b)
return a;
return gcd (b, a % b);
}
LL lcm (LL a, LL b){//最小公倍数
return a * b / gcd (a, b);
}
void dfs (int k, int Index, LL v){//k代表第几次并集，Index代表到了第几个集合，v代表这个集合，如v=8，就代表8的倍数这个集合
if (v > b)//超出范围就没有意义
return ;
if (k % 2 == 0)//第偶数次加，第基数次减
ans += b / v - a / v;
else
ans -= b / v - a / v;
for (int i = Index + 1; i <= n; i ++){
LL t = lcm (v, m[i]);//求着两个集合的并集
dfs (k + 1, i, t);//递归求解
}
}
int main (){
scanf ("%d", &n);
for (int i = 1; i <= n; i ++)
scanf ("%d", &m[i]);
scanf ("%d %d", &a, &b);
dfs (0, 0, 8);//从第0次开始
printf ("%lld\n", ans);
return 0;
}
4.感想
这道题的深搜是最考验人的，有时候只要带一些例子进去算一下就豁然开朗了。