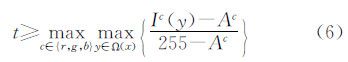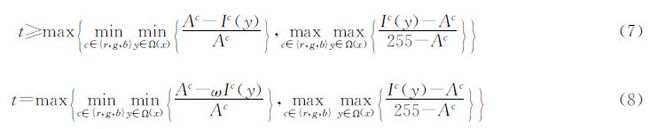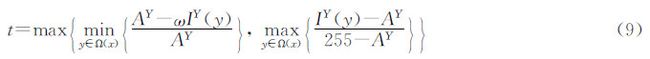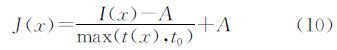图像和视频的快速去雾算法研究

王昕, 孙莹莹, 李影昉. 图像和视频的快速去雾算法研究[J]. 影像科学与光化学, 2016, 34(1): 82-87.  

WANG Xin, SUN Yingying, LI Yingfang. Fast Haze Removal for Real-time Image and Video[J]. Imaging Science and Photochemistry, 2016, 34(1): 82-87.  

图像和视频的快速去雾算法研究

王昕 ¹   , 孙莹莹 ¹, 李影昉 ²    

摘要：雾、霾等恶劣天气会导致室外图像能见度和对比度降低。虽然可以通过增强有雾图像的对比度得到清晰的图像,但对比度的过度增强可能会截断像素值,造成信息丢失。因此,本文基于信息丢失问题提出了一种快速、优化的去雾算法。通过最小化信息丢失,使输出图像不仅能保留较多的细节,且具有较高的对比度。此外,通过将RGB颜色空间转换为YUV颜色空间,仅对亮度分量Y进行处理,提高了算法的运算速度。算法的对比实验结果表明,本文的算法不仅去雾效果明显,而且运算速度快,完全能满足视频去雾的实时性要求。

关键词：  图像去雾      视频去雾      引导滤波      透射率    

Fast Haze Removal for Real-time Image and Video

WANG Xin ¹   , SUN Yingying ¹, LI Yingfang ²    

Abstract: Outdoor image often lose visibility and contrast due to the presence of haze. To effectively enhance the degraded haze image, we can get clear image by enhancing haze image's contrast. However, the excessive enhancement of the degraded contrast may truncate pixel values and cause information loss. Therefore, we proposed a fast and optimized dehazing algorithm based on information loss. By minimizing the information loss, the output image not only has high contrast but also has very little information loss. Moreover, we convert RGB color space into YUV color space, and only process the luminance component. This greatly improves the computational speed, thus suitable for processing video sequence. The contrast experimental results show that the proposed algorithm can effectively remove haze and the computing speed is fast, which can fully meet the real-time requirement for the removal of video haze.

Key words:  image dehazing      video dehazing      guide filter      transmittance    

近年来，雾、霾天气频繁出现，在这种恶劣天气条件下，物体的反射光会被大气中的混浊介质吸收和散射，导致捕获的室外图像和视频可见度低，细节模糊，色彩失真，严重影响图像处理系统的性能。因此，图像去雾算法的研究具有非常大的实际意义。视频去雾算法对实时性要求极高，快速去雾算法的研究也极为重要。

国内外学者近年主要研究单幅图像的去雾算法，视频去雾算法的研究很少且不成熟，这是因为图像去雾算法的复杂度较高，且处理时间较长。目前，最常用的去雾方法基于图像增强理论，如直方图均衡化、局部对比度增强、伽马校正等。直方图均衡化通过拉伸直方图，来提高图像的对比度^[1]，从而达到图像去雾的目的。这种算法虽然简单，实时性好，但是对比度增强力度相对较低。Tan^[2]基于无雾图像的对比度比有雾图像要高的事实，通过最大化局部对比度实现了图像去雾，但复原后的图像容易产生色调偏移和颜色失真。其他去雾方法基于图像复原理论，通过建立图像退化模型来对有雾图像进行复原。利用建立物理模型的方法虽然能得到理想的复原图像，但通常需要场景深度或环境光等额外信息。Fatta^[3]假设景物表面阴影和介质透射率局部不相关，利用独立成分分析方法和马尔科夫随机场模型实现去雾，

但该方法对浓雾图像的复原结果存在较大失真。Tarel等^[4]采用中值滤波方法去除雾气遮罩，但中值滤波器的性质会使复原图像在景深发生突变的边缘产生光晕效应。He等^[5]提出一种基于暗通道先验理论的单幅图像去雾算法，假定在绝大多数非天空的局部区域里，某一些像素至少有一个颜色通道具有很低的值。文中还利用抠图技术对透射率修正，使输出图像更加清晰自然。然而，对于图像中较亮的区域，如天空和白色物体，这一假定并不成立。

对于视频去雾，Oakley等^[6]假定图像中所有像素的场景深度相似，并从所有像素中减去相同的偏移值。Zhang等^[7]首先估计出每一帧视频序列的深度图，然后利用空间和时间的相似性对深度图进行修正。这些算法复杂度较低，但不适用于场景深度有变化的图像。此外，传统的视频去雾算法运算时间较长，复原后的无雾视频质量不高。因此，提出一种有效的实时视频去雾算法有很大实际意义。

在本文中，基于信息丢失提出了一种实时图像和视频去雾算法。首先，利用改进的Patch Retinex White算法计算环境光。其次，通过最小化信息丢失估算出最优的透射率，并使用引导滤波^[8]对透射率进行修正和细化，去除光晕和块效应。对于视频去雾方法，将RGB颜色空间转换为YUV颜色空间，仅处理亮度(Y)分量，不对色度(U,V)分量做任何处理，以降低计算复杂度。结合物理模型以及求得的透射率和环境光，可以有效且快速地得到无雾图像。

1 大气散射模型

有雾图像的退化过程可以用大气散射模型^[4,6]表示。该模型由衰减模型^[9]和环境光模型^[10]两部分组成，模型表达式为：

其中，x为图像像素的空间坐标,I(x)是观察到的有雾图像,J(x)是去雾后的图像,A表示环境光,t(x)表示透射率，用来描述光线通过传输介质到达相机的过程中没有被散射的部分，t(x)和场景深度成反比，可以表示为：

其中,β为大气散射系数；d为场景深度，即场景和相机之间的距离。如果能求出透射率，就可以得到场景深度。

图像和视频去雾去雾的目的就是根据已知的输入图像I(x)恢复出无雾图像J(x)，在此过程中需要首先估计出环境光A和透射率t(x)，然后通过反解大气散射模型得到输出图像J(x)。

1.1 估计环境光

根据原始Patch Retinex White算法^[11]，环境光和图像中最亮的像素点相对应。但是，当图像中存在较亮的物体时，环境光的估计值不够准确。本文采用改进的Patch Retinex White算法估计环境光。改进后的方法不再根据图像中的最亮点来估计环境光，而是求图像各个颜色通道的累积直方图，取累计到某一个值P*N时对应的像素值作为环境光。其中P为百分值，实验中取为1%~5%，N位图像的像素总数。通过实验结果可知这种简单算法的鲁棒性更好。环境光的估计值较准确，复原后远处的浓雾区域不会过亮，近处的物体也不会很暗。本文中的实验均是使用这种算法来估计环境光。

1.2 估计透射率

通过增强的有雾图像的对比度，可以得到清晰的无雾图像。然而，由于过度增强，一些像素值会出现溢出现象，并被截断为0或255。这将导致无雾霾图像的信息丢失。通过最小化信息损失，可以找到最优的透射率。在极端的情况下，最佳的透射率不会产生任何信息丢失，对应的不等式是：

其中，J^c是无雾图像J的一个颜色通道，Ω(x )是以像素点x为中心的局部区域。本文假定在局部区域里，透射率是一个常量。在每个尺寸大小为15×15局部区域里，求出一个固定的透射率。结合上面的不等式和公式(1)，可以得到两个关于透射率的约束条件如式(5)、式(6)所示。

将这两个约束条件进行合并，得到式(7)。

由于对比度和透射率成反比，透射率越小对比度越大，图像越清晰。因此，最优的透射率是满足公式(7)的最小值，如式(8)所示。

如果将雾全部去掉，图像会因失去深度感并显得不自然。因此，通过引入一个常量参数ω，可以保留远处的少量雾气。在本文试验中，参数ω的值均取为0.95。

对于视频序列，将有雾图像序列的RGB颜色空间转换为YUV颜色空间，不改变色度(U,V)分量，只对亮度(Y)分量进行去雾处理。根据实验结果我们发现，利用这种方法得到的去雾结果可以和在RGB颜色空间得到的去雾结果相媲美；并且和亮度分量相比，色度分量受雾气影响很小。同时，计算时间和复杂度大大降低，可达到实时性要求。因此，对于视频序列，可以得到第k帧图像的透射率，如式(9)所示。

事实上，局部区域内的透射率并不是一个不变的常亮，根据上面算法得到的透射率图会出现光晕和块效应，需要对透射率进一步修正。在本文中，采用引导滤波算法^[8]来细化透射率，获得更准确的透射率图。

1.3 去雾

估计出环境光和透射率后，可以通过解公式(10)得到无雾图像和视频序列。

当透射率t的值很小时，无雾图像的噪声会被放大。因此，一般设置一个最小值t₀，当t小于t₀时，令t=t₀，实验中t₀取为0.1。

2 实验结果

本实验在操作系统为Windows XP、处理器主频为2.53 GHz、系统内存为1 G的PC机上运行。用本文算法、He算法对图1(a)中 “snow,”“house”和“buildings”图像进行去雾处理，并对处理后的结果做了比较。由图像“snow”可以看出，He去雾算法不适用于包含天空的图像，会在天空区域出现颜色失真，而利用本文算法得到结果图像在天空区域的颜色过度自然。图像“house”中的雾气较浓，本文算法仍能有效去除部分雾气，提高图像的能见度。图像“buildings”比较复杂，根据He算法得到的结果图像去雾效果较好，但计算时间长、复杂度高、色调偏暗，并存在细节丢失；用本文算法得到的无雾图像则能保留更多的细节，且亮度适中。

图1 本文算法与He算法的比较 (a) 输入图像，上：图像 “snow”，中：图像“house”，下：图像“buildings”；(b) He算法；(c) 本文算法Comparison with He’s method (a) input image. Top: “snow” image. Middle: “house” image. Bottom: “buildings” image,(b)He’s result,(c) our result

为了进一步客观地验证本文算法的有效性，采用信息熵、平均梯度作为图像质量的度量指标，度量结果如表1所示。

表1 不同算法处理结果比较Result obtained different algorithms

平均梯度又称为清晰度，它可以描述影像的清晰程度，反映了图像细节反差程度和纹理变化特征，一般来说，平均梯度值越大表明图像越清晰。而图像的信息熵反映了图像中平均信息量的多少，信息熵越大表明图像自身信息更丰富。从表中可以看出，本文算法的各项度量指标均高于He算法，这从客观上表明由本文算法的有效性。

我们还对图2和图3中的“Intersection”和“Road”视频进行了去雾处理。从实验结果可以看出，本文算法可以有效地去除视频序列中的雾气。用本文算法对1000帧分辨率为600×400的视频序列进行处理，处理速度约为25帧～28帧每秒，能够满足实时性的要求。

图2 对视频“Road”的去雾结果 (a) 输入视频,(b) 去雾后的视频,从左到右分别是第17、19和21帧Video dehazing on the “Road” sequence (a) the input haze sequences,(b) the dehazed sequences The frame numbers of the left,middle,and right columns are 17,19,and 21,respectively

图3 对视频“Intersection”的去雾结果 (a) 输入视频,(b) 去雾后的视频,从左到右分别是第17、19和21帧Video dehazing on the “Intersection” sequence (a) the input haze sequences,(b) the dehazed sequences The frame numbers of the left,middle,and right columns are 17,19,and 21,respectively

3 结语

本文提出一种简单而快速的图像和视频去雾算法。首先，利用改进的Patch Retinex White理论计算出环境光，然后，通过最小化信息丢失求得最优的透射率，最后，根据大气散射模型求出无雾图像和视频序列。实验结果表明，该算法能有效去雾，并且能实现实时性。

参考文献

[1]	Stark J A. Adaptive image contrast enhancement using generalization of histogram equalization[J]. IEEE Transactions on Image Processing, 2000,9(5): 889-896.
[2]	Tan K, Oakley J P. Physics-based approach to color image enhancement in poor visibilityconditions[J]. Optical Society of America, 2001,18(10):2460-2467.
[3]	Fattal R. Single image dehazing[J]. ACM Transactions on Graphics, 2008,27(3): 72-80.
[4]	Tarel J, Hautiere N, Fast visibility restoration from a single color or gray level image[C]. Proceedings of the 12th IEEE International Conference on Computer Vision, Japan, 2009: 1701-1708.
[5]	He K M, Sun J, Tang X O. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011,33(12): 2341-2353.
[6]	Oakley J, Hong B. Correction of simple contrast loss in color images[J]. IEEE Transactions on Image Processing, 2007,16(2): 511-522.
[7]	Zhang J W, Liang L. Video dehazing with spatial and temporal coherence[J]. Visual Computer, 2011,27(6):749-757.
[8]	He K M, Sun K, Tang X O. Guided image filtering[J]. Pattern Analysis and Machine Intelligence, 2013,35(6): 1397-01409.
[9]	Tan R. Visibility in bad weather from a single image[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Washington, USA, 2008, 23-28.
[10]	Koschmieder H. Theorie der horizontalen sichtweite[J]. Beitr. Phys. Freien Atm., 1924,12(3):171-181.
[11]	Marc Ebner. A Parallel algorithm for color constancy[J]. Journal of Parallel and Distributed Computing, 2004,64(1):79-88.