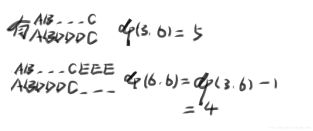线性DP

放苹果 POJ - 1664

题意：把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

思路：设 dp[i][j]表示在 i 个盘子中，放置 j 个苹果的方案数

• 当 i > j 时，注意到题目中取的是组合数，$dp[i][j]=dp[j][j]$，多余的盘子并没有任何影响
• 当 i < j 时，可以选择有空盘和无空盘的方法，有空盘时，即第 i 个位置不放，$dp[i][j]=dp[i-1][j]$。第 i 个位置放时，我们需要求的是组合数，所以可以往每个盘子里放一个苹果，此时还剩 j - i 个苹果。dp[i][j]=dp[i][j-i]，相当于在 i 个盘子里放 j -i 个苹果的方案数。

#include <cstdio>
using namespace std;

int t,n,m;
int dp[20][20];

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&m,&n);
        for(int i=1;i<=n;++i) dp[i][0]=1;
        for(int i=1;i<=n;++i)
        {
            for(int j=1;j<=m;++j)
            {
                if(i>j) dp[i][j]=dp[j][j];
                else dp[i][j]=dp[i-1][j]+dp[i][j-i];
            }
        }
        printf("%d\n",dp[n][m]);
    }
    return 0;
}

Number String HDU - 4055

链接：http://acm.hdu.edu.cn/showproblem.php?pid=4055

题意：给定一个字符串，$I$ 表示本字符要比前一个字符大，$D$ 表示比前一个字符小，？表示可大可小，有多少满足条件的排列

思路：设 $dp[i][[j]$表示排列长度为 i 以 j 结尾的排列数

• 遇到 $I$，$dp[i][j]={\sum }_{k=1}^{j-1}dp[i-1][k]=dp[i][j-1]+dp[i-1][j-1]$
• 遇到 $D$，$dp[i][j]={\sum }_{k=j}^{i-1}dp[i-1][k]=dp[i-1][j]+dp[i][j+1]$，从 j 开始，是因为原本的数只有 i -1 个，现在多了一个，且把 j 放在了最后，那么原本是 j 到 i - 1之间的数，就可以看成是 j +1 到 i
• 遇到 $?$，$dp[i][j]={\sum }_{j=1}^{i-1}dp[i-1][j]$

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2000+10,mod=1e9+7;

int dp[maxn][maxn];
char s[maxn];

int main()
{
    while(~scanf("%s",s+2))
    {
        int n=strlen(s+2)+1;
        ll sum=1;
        memset(dp,0,sizeof(dp));
        dp[1][1]=1;
        for(int i=2;i<=n;++i)
        {
            if(s[i]=='I')
            {
                for(int j=1;j<=i;++j)
                    dp[i][j]=(dp[i][j-1]+dp[i-1][j-1])%mod;
            }
            else if(s[i]=='D')
            {
                for(int j=i;j>=1;--j)
                    dp[i][j]=(dp[i][j+1]+dp[i-1][j])%mod;
            }
            else
            {
                for(int j=1;j<=i;++j)
                    dp[i][j]=sum;
            }
            sum=0;
            for(int j=1;j<=i;++j)
                sum=(sum+dp[i][j])%mod;
        }
        ll ans=0;
        for(int i=1;i<=n;++i)
            ans=(ans+dp[n][i])%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

顺序对齐（Align）-动态规划-中高级

Description

考虑两个字符串右对齐的最佳解法。例如，有一个右对齐方案中字符串是AADDEFGGHC和ADCDEGH。

AAD_DEFGGHC

ADCDE__GH_

每一个数值匹配的位置值2分，一段连续的空格值-1分。所以总分是匹配点的2倍减去连续空格的段数，在上述给定的例子中，6个位置（A，D，D，E，G，H）匹配，三段空格，所以得分2*6+(-1)*3=9，注意，我们并不处罚左边的不匹配位置。若匹配的位置是两个不同的字符，则既不得分也不失分。

请你写个程序找出最佳右对齐方案。

Input

输入文件包含两行，每行一个字符串，最长50个字符。字符全部是大字字母。

Output

一行，为最佳对齐的得分。

Sample Input

AADDEFGGHC
ADCDEGH
Sample Output
9

链接:http://acm.zjnu.edu.cn/CLanguage/showproblem?problem_id=1273

思路：

• $dp[i][j]$ 表示 $s1$ 的前 $i$ 个字符和 $s2$ 的前 $j$ 个字符，最佳匹配的最大得分

• 当 $s1[i]=s2[j]$ 时，显然 $dp[i][j]=dp[i-1][j-1]+2$

• 当 $s1[i]!=s2[j]$ 时，分三种情况

  $s1[i]$和$s2[j]$两个字符直接匹配，无空格，此时 $dp[i][j]=dp[i-1][j-1]$

  $s1[i]$和$s2[j]$两个字符不匹配，$s1[i]$ 与空格匹配，则$s2[j]$一定在前面与，s1[ 1~i-1]匹配过了，$dp[i][j]=max(dp[i][j],dp[k][j]-1)$

  $s1[i]$ 和$s2[j]$两个字符不匹配，s2 [ j ] 与空格匹配，则s1 [ i ]一定在前面与，s2[ 1~j-1]匹配过了，$dp[i][j]=max(dp[i][j],dp[i][k]-1)$

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1000+10,mod=1e9+7;

int dp[maxn][maxn];
char s1[maxn],s2[maxn];

int main()
{
    scanf("%s %s",s1+1,s2+1);
    int n=strlen(s1+1);
    int m=strlen(s2+1);
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            if(s1[i]==s2[j]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+2);
            else
            {
                dp[i][j]=max(dp[i][j],dp[i-1][j-1]);
                for(int k=1;k<i;++k)
                    dp[i][j]=max(dp[i][j],dp[k][j]-1);
                for(int k=1;k<j;++k)
                    dp[i][j]=max(dp[i][j],dp[i][k]-1);
            }
        }
    }
    printf("%d\n",dp[n][m]);
    return 0;
}

思路2：
设f[i][j]表示s1中第i个跟s2中第j个匹配时的最大得分。我们知道两个字串在同样的位置出现空格不是最优的。这样的话，f[i][j]就只能由f[i−1][k]和f[k][j−1]推出来，最后统计答案就行了

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <memory.h>
#include <queue>
#include <vector>
#include <set>
#include <string.h>
#include <cmath>
#define rep(i,a,b) for (int i=a; i<=b; ++i)
#define per(i,b,a) for (int i=b; i>=a; --i)
#define mes(a,b)  memset(a,b,sizeof(a))
#define ll long long
using namespace std;
const int maxn=1e5;

//为什么这样写出来的，是右对齐的？
//因为我们永远在找，最大得分的情况，在最左边的空格是筛选不到的
//也就因此成了右对齐 

int main()
{
	char a[55],b[55];
	int len1,len2,f[55][55],ans=0;
	
	cin>>a+1>>b+1;
	len1=strlen(a+1);
	len2=strlen(b+1);	
	mes(f,0);
	rep(i,1,len1)
		if(a[i]==b[1])
			f[i][1]=2;
	rep(i,1,len2)
		if(b[i]==a[1])
			f[1][i]=2;
	
	for(int i=2;i<=len1;++i)
	{
		for(int j=2;j<=len2;++j)
		{
			f[i][j]=f[i-1][j-1];
			//j-1和j之间有空格的情况，j-1与i前面的某个位置匹配 
			for(int k=1;k<i-1;++k)
				f[i][j]=max(f[k][j-1]-1,f[i][j]);
			//i-1和i之间有空格的情况，i-1与j前面的某个位置匹配 
			for(int k=1;k<j-1;++k)
				f[i][j]=max(f[i-1][k]-1,f[i][j]);
			if(a[i]==b[j])
				f[i][j]+=2;
		}
	}
	//如果是最后的话，就不用减分了 
	rep(i,1,len1)
		ans=max(ans,f[i][len2]-1*(i!=len1));
	rep(j,1,len2)
		ans=max(ans,f[len1][j]-1*(j!=len2));
	cout<<ans<<endl;	
	return 0;
}

codevs 1300：文件排版（DP）

参考链接:https://www.cnblogs.com/Friends-A/p/11054969.html

题意：给定每行的宽度，给定一堆单词，让你给这些单词排版使得难看程度最小。难看程度计算方式，如果一个空白段有n个空格，那么它的难看程度为 $(n-1{)}^2$

输入
28
This is the example you are
actually considering.

排版后结果为：
This is the example you
are actually considering.
输出
Minimal badness is 12.

思路：题目规定每一行的开始和结束必须是单词，因此设 $dp[i]$ 表示以第 i 个单词为当前行结尾的最小难看程度。

• 枚举 i 前面的单词 j ，假设它为上一行的结尾，那么 $dp[i]=min(dp[i],dp[j]+cost(i,j)$

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1000+10,inf=1e9+7;

int n;
int dp[maxn];
int len[maxn],cnt;
char s[maxn];

int cost(int i,int j)
{
    if(i==j+1)
    {
        if(len[i]-len[i-1]==n) return 0;
        return 500;
    }
    int seg=i-j-1;
    int tot=n-(len[i]-len[j]);
    if(tot<seg) return inf;
    int avg=tot/seg;
    int r=tot%seg;
    return r*avg*avg+(seg-r)*(avg-1)*(avg-1);
}

int main()
{
	memset(dp,0x3f,sizeof(dp));
    cin>>n;
    while(~scanf("%s",s))
        len[++cnt]=len[cnt-1]+strlen(s);
    dp[0]=0;
    for(int i=1;i<=cnt;++i)
        for(int j=0;j<i;++j)
            dp[i]=min(dp[i],dp[j]+cost(i,j));
    printf("Minimal badness is %d.\n",dp[cnt]);
    return 0;
}

Post Office POJ - 1160

链接：http://poj.org/problem?id=1160
题意：在 n 个村庄上建 p 个邮局使得所有村庄到自己最近的邮局的距离之和最短

思路：

• 设 $dp[i][j]$ 表示前 i 个村庄建立 j 个邮局的最短距离。
• 设 $dis[i][j]$ 表示在第 i 个村庄和第 j 个村庄之间建立一个邮局的最短距离
• 只所以这样设定 dis，是因为在转移的时候需要用到
• $dp[i][j]=dp[k][j-1]+dis[k+1][i]$
• $dis[i][j]$ 可以在 $dis[i][j-1]$ 的基础上推导。

#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
using namespace std;
const int maxn=1000+10,inf=1e9+7;

int p,n;
int dis[310][310];
int dp[310][35];
int a[310];

int main()
{
    scanf("%d%d",&n,&p);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]);
    for(int i=1;i<=n;++i)
        for(int j=i+1;j<=n;++j)
            dis[i][j]=dis[i][j-1]+a[j]-a[(i+j)/2];

    memset(dp,0x7f,sizeof(dp));
    for(int i=1;i<=n;++i) dp[i][1]=dis[1][i];
    for(int i=2;i<=n;++i)
        for(int j=1;j<=min(i,p);++j)
            for(int k=j-1;k<i;++k)
                dp[i][j]=min(dp[i][j],dp[k][j-1]+dis[k+1][i]);
    printf("%d\n",dp[n][p]);
    return 0;
}

Alphacode POJ - 2033

链接：http://poj.org/problem?id=2033
题意：给定一串数字，A代表 1，B代表 2，等等。问有多少种方式翻译成英文
思路：设 $dp[i]$ 表示在前 i 个字符翻译成英文的方式。要么就是第 i 位单独组成一个英文字母，要么就是第 i 位和第 i - 1 位同时组成一个字母

#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
using namespace std;
const int maxn=10000+10,inf=1e9+7;

ll dp[maxn];
char s[maxn];

int main()
{
    while(scanf("%s",s+1))
    {
        int n=strlen(s+1);
        if(n==1&&s[1]=='0') break;
        memset(dp,0,sizeof(dp));
        dp[0]=1,dp[1]=1;
        for(int i=2;i<=n;++i)
        {
            if(s[i]!='0')
                dp[i]=dp[i-1];
            if(s[i-1]=='2'&&s[i]<='6'||s[i-1]=='1')
                dp[i]+=dp[i-2];
        }
        printf("%lld\n",dp[n]);
    }
    return 0;
}