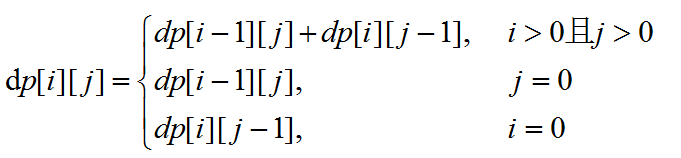程序基本算法习题解析 动态规划-过河卒

题目：

A点有一个过河卒，需要走到目标B点。卒可以向下或者向右走。同时在棋盘上任意一点有一个对方的马，该马所在的点和马跳跃一步可达的所有点称为马的控制点。棋盘用坐标表示，A点(0,0)、B点(n,m)（n,m为不超过20的整数，并由键盘输入），马的位置坐标也要给出（约定：C不等于A，同时C不等于B）。要求计算出卒从A点能够到达B点的路径的条数。输入B点的坐标(n,m)(1<=n,m<=14)以及对方马的坐标(x,y)，输出路径的条数。

思路：

可以定义一个数组dp，dp[i][j]表示到达点(i,j)的路径条数，而dp[i][j]的递推公式为：

而对方马的位置及其控制点处，卒不可能达到，因此那些位置处的dp[i][j] = 0。

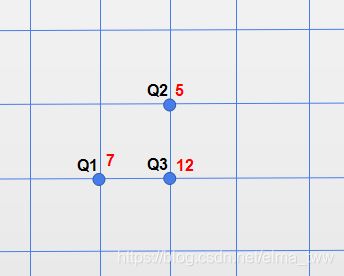
对于这个递推公式，其实很好理解，因为卒只能往下和往右走，因此到达点(i,j)的路径条数等于到达它上方(i,j-1)和到达它左方(i-1,j)的路径和。例如下图，若要到达Q3，上一步必须到达Q1或Q2,因此到达Q3的路径等于到达Q1和Q2的路径和。

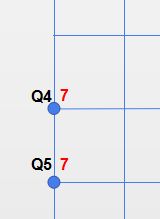
而在横轴或纵轴上的点就稍有不同，例如下图（纵轴上的点）,若要到达Q5，上一步必须到达Q4（卒只能往下和往右走），因此到达Q4的路径等于到达Q3路径。横轴上的点也一样。

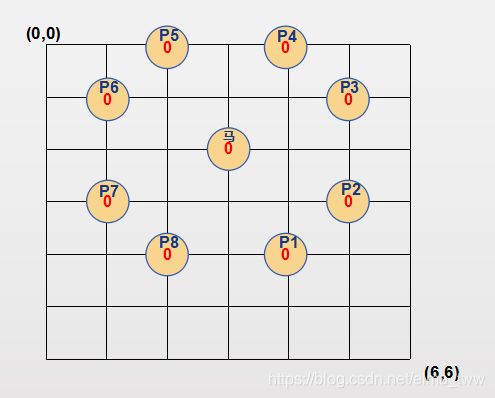
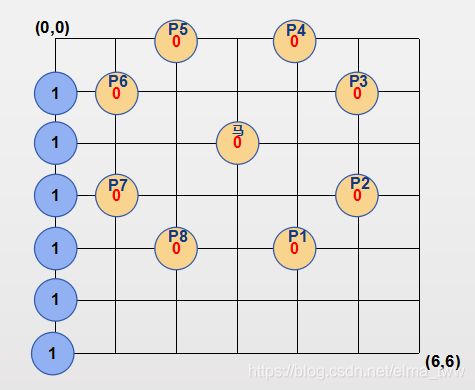
现在以B点坐标为(6,6)，马的位置为(3,2)示例如何求路径。需要注意的是，题目的意思是当卒移动到马的控制点时，马才去吃卒，其它时间默认只动卒而不动马（可能对方动其它棋子去了），刚看到题时，可能以为就卒和马在动，卒动一次，马动一次，然后马每下一步，控制点还会变动。本题没有这么复杂，就只需考虑当前马的控制点即可。 

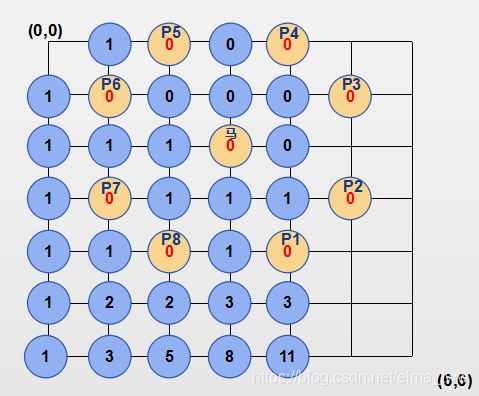
首先将所有点的dp[][]初始化为1（图中未标出），对于每个点(i,j) ，圆圈内的数字表示dp[i][j]。首先当前马的位置和其控制点处卒不可能到达，因此这些位置的dp[][]为0。

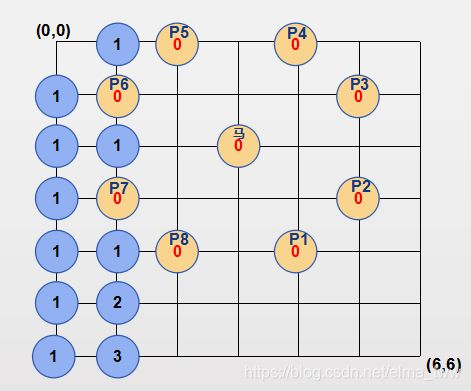
从横轴（i）开始遍历（外循环）,先将竖向（j）填满（内循环），第一列 i = 0，因此递推公式为dp[i][j] = dp[i][j-1]。

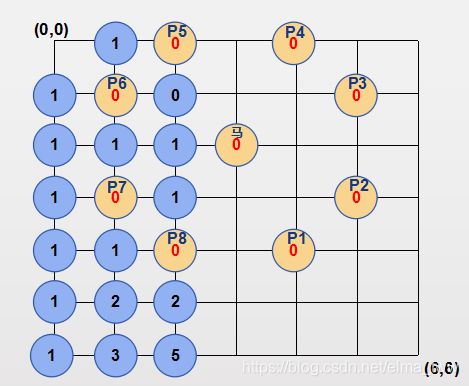
第二列，（第二列的第一个点是因为初始化为1 ），其它点满足 i 和 j 都不为0，因此用dp[i][j] = dp[i-1][j] + dp[i][j-1]这个递推公式。后面几列求法相同。

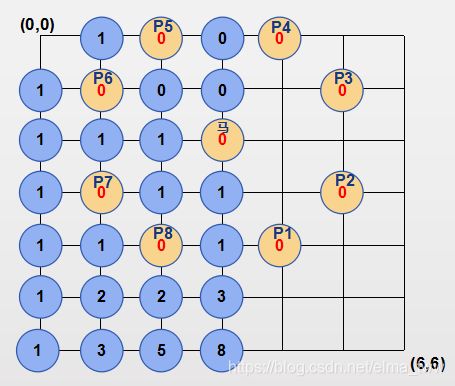
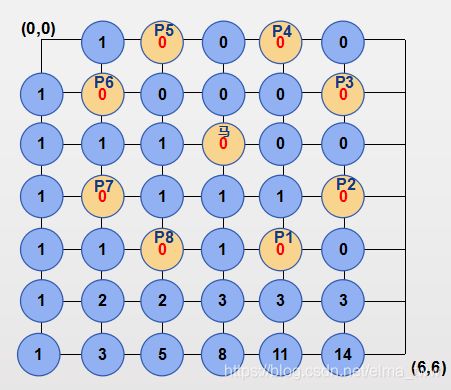
这就是最终的解。卒从原点到达任意一点的路径条数都已求出，那么卒从A点（原点）到达B点（6,6）的路径条数 即为dp[6][6]。

代码如下：

// Chapter14_2.cpp : Defines the entry point for the application.
// 过河卒
// A点有一个过河卒，需要走到目标B点。卒可以向下或者向右走。同时在棋盘上任意一点有一个对方的马，
// 该马所在的点和马跳跃一步可达的所有点称为马的控制点。棋盘用坐标表示，A点(0,0)、B点(n,m)
// （n,m为不超过20的整数，并由键盘输入），马的位置坐标也要给出（约定：C不等于A，同时C不等于B）。
// 要求计算出卒从A点能够到达B点的路径的条数。
// 输入B点的坐标(n,m)(1<=n,m<=14)以及对方马的坐标(x,y)。
// 输出路径的条数

#include "stdafx.h"
#include
using namespace std;

int main()
{
	int bx,by,mx,my;
	cout << "输入B点的坐标：";
	cin >> bx >> by;
	cout << "输入对方马的坐标：";
	cin >> mx >> my;
	//dp[i][j]表示到达点(i,j)的路径条数
	int dp[14][14];
	int i,j;
	//初始化dp数组（全部赋为1）
	for(i=0;i<=bx;i++)
		for(j=0;j<=by;j++)
			dp[i][j] = 1;
	//马的控制点处（包括马的位置）的dp初始化为0
	//注意，因为马的位置的关系，有些控制点可能跳出棋盘而达不到
	if(mx+1 <= bx && my+2 <= by)
 		dp[mx+1][my+2]=0; //P1点
	if(mx+2 <= bx && my+1 <= by)
		dp[mx+2][my+1]=0; //P2点
	if(mx+2 <= bx && my-1 >= 0)
		dp[mx+2][my-1]=0; //P3点
	if(mx+1 <= bx && my-2 >= 0)
		dp[mx+1][my-2]=0; //P4点
	if(mx-1 >= 0 && my-2 >= 0)
		dp[mx-1][my-2]=0; //P5点
	if(mx-2 >= 0 && my-1 >= 0)
		dp[mx-2][my-1]=0; //P6点
	if(mx-2 >= 0 && my+1 <= by)
		dp[mx-2][my+1]=0; //P7点
	if(mx-1 >= 0 && my+2 <= by)
		dp[mx-1][my+2]=0; //P8点
	dp[mx][my]=0; //当前马的位置
	//卒向右走
	for(i=0;i<=bx;i++)
	{
		//卒向下走
		for(j=0;j<=by;j++)
		{
			//如果没有走到对方马的控制点
			if(!dp[i][j])
				continue;
			else if(i==0 && j == 0)
				continue;
			//当卒在横轴上时(y=0)
			else if(j == 0)
				dp[i][j] = dp[i-1][j]; 
			//当卒在纵轴上时(x=0)
			else if(i == 0)
				dp[i][j] = dp[i][j-1];
			//到达点(i,j)的路径条数等于到达它上方(i,j-1)和到达它左方(i-1,j)的路径和
			else 
				dp[i][j] = dp[i-1][j]+dp[i][j-1];
		}
	}
	/*
	for(j=0;j<=bx;j++)
	{
		for(i=0;i<=by;i++)
			cout << dp[i][j] << ' ';
		cout << endl;
	}
	*/
	cout << "到达B点的路径条数为:" << dp[bx][by] << endl;
	system("pause");
	return 0;
}

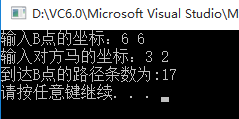
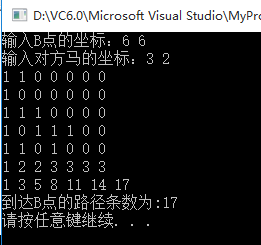
运行结果如下：

若是想看其它点的路径条数，可以将以上程序加注释的部分放开，即

for(j=0;j<=bx;j++)
	{
		for(i=0;i<=by;i++)
			cout << dp[i][j] << ' ';
		cout << endl;
	}

运行结果如下：

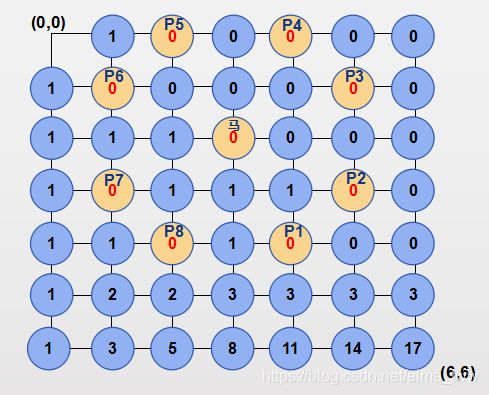
可见，和我们之前手算的结果是一样的。