程序基本算法习题解析 给定由n个整数（可能为负数）组成的序列a1,a2,...,an,求该序列的字段和的最大值。

这是动态规划法中的一道题，感觉很复杂，但是稍后看到程序会惊讶于它的简洁。

先附上代码：

// Chapter8_4.cpp : Defines the entry point for the application.
// 给定由n个整数（可能为负数）组成的序列a1,a2,...,an,求该序列的字段和的最大值。
// 当所有整数均为负整数时定义其最大字段和为0。

#include "stdafx.h"
#include
using namespace std;

const int N = 8;
int main()
{
	//定义一个数组存放序列数
	int arr[N] = {-1,2,5,4,-7,6,8,-2};
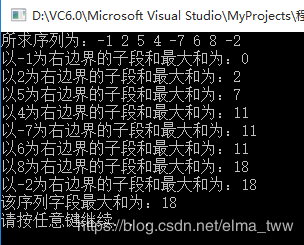
	cout << "所求序列为：";
	for(int k=0;k

注释已经比较详细了，抽象讲解会把人绕晕，因此就以“-1,2,5,4,-7,6,8,-2”这个序列为例来分析。里面的每个元素都会被作为子序列的右边界进行计算求解。首先计算以第一个数（-1）为右边界的子段最大和，因为其只有一个数，因此它的值就为该序列的子段最大和，即程序中的proSum=-1，和maxSum进行比较，小于maxSum，因为maxSum还是保持它的初始值0不变；再计算以第二个数（2）为右边界的子段最大和，因此添加该元素之前的子序列的子段最大和为负，那么不管即将添加的元素为多少，都需要将之前的子序列舍弃，直接取该元素的值作为新序列的子段最大和，即proSum=2,和maxSum进行比较,大于maxSum，因此将proSum的值赋给maxSum，此时maxSum=2；...以‘4’为右边界的子段最大和为11（maxSum=11）；计算以‘-7’为右边界的子段最大和，添加‘-7’这个元素后proSum变成了4，小于maxSum，因此maxSum保持不变；计算以‘6’为右边界的子段最大和，添加‘6’这个元素后proSum变成了10，依然小于maxSum，maxSum继续保持不变；计算以‘8’为右边界的子段最大和，添加‘6’这个元素后proSum变成了18，大于maxSum，因此把proSum的值赋给maxSum，此时maxSum=18；...

运行结果如下（为了方便理解，把计算过程也打印了出来）：