程序基本算法习题解析 找出从自然数1~n中任取r个元素的所有组合。

要求输入n和r，输出r个元素的所有组合。

思路：

可使用分治法（递归法）求解该题，步骤如下：

选取1~n中某个整数为该组合的第一个数，对剩下r-1个数进行组合；再从剩下的n-1个数中，选取某个整数为该组合的第2个数，对剩下的r-2个数进行组合；...，直到选取了r个数，此时，输出该组合结果。

为了不重复选取，可从小到大的选取整数，保证组合中的整数是逐渐增大的。例如，选取3作为组合中的第一个数，则后面的数应从4~n中选取。

代码如下：

// Chapter13_2.cpp : Defines the entry point for the application.
// 找出从自然数1~n中任取r个元素的所有组合
// 输入n和r
// 输出r个元素的所有组合

#include "stdafx.h"
#include
using namespace std;
//求组合的函数
//chosen:要输出的数组（r个元素），begin:子数组的第一个元素在原数组中的位置（角标加1）
// n:自然数个数，r:选取的个数，count:计数变量
void funChoose(int *chosen,int begin,int n,int r,int count)
{
	//如果已经选了r个数，则输出所选数值并返回
	if(count > r)
	{
		for(int j=1;j<=r;j++)
			cout << chosen[j] << ' ';
		cout << endl;
		return;
	}
	//如果还未选出r个数，则从小到大进行选取
	for(int i=begin;i<=n;i++)
	{
		chosen[count] = i;
		//递归时，从i的下一个数开始
		funChoose(chosen,i+1,n,r,count+1);
	}
}
int main()
{
	int n,r;
	cout << "输入n和r：";
	cin >> n >> r;
	int *chosen = new int[r+1];
	cout << "组合方式有：" << endl;
	funChoose(chosen,1,n,r,1);
	delete [r]chosen;
	system("pause");
	return 0;
}

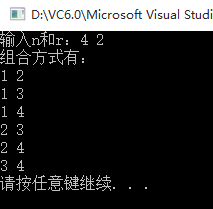
运行结果如下：