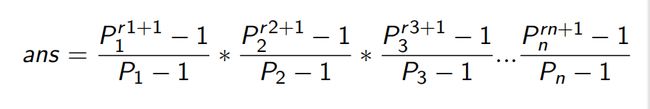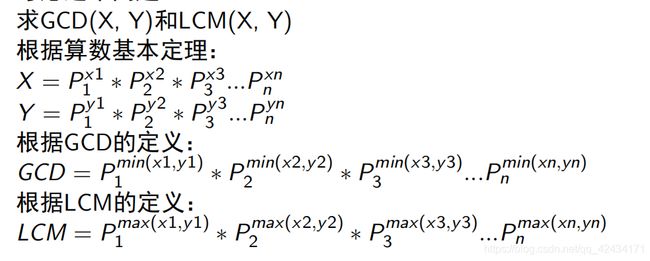算术基本定理

算术基本定理,又称为正整数的唯一分解定理,即:每个大于1的自然数均可写为质数的积,而且这些素因子按大小排列之后,写法仅有一种方式。

例如：90=2*3^2*5

（pi是质数且ri>=0）

代码实现：复杂度:

 #include
#include
#include

求N的因子个数：

               根据算术基本原理：

               根据排列组合可得：

                 

解释：这个式子：例如1+r1  就是p1的选择有0个至r1个，有1+r1种情况，其他的一个道理，最后把它们乘起来，主要是运用了排列组合

例如：20=2^2*5^1

因子个数ans=（1+2）*（1+1）=6（1,2,4,5,10,20）

1 :2^0*5^0;
5 :2^0*5^1;
2 :2^1*5^0;
10:2^1*5^1;
4 :2^2*5^0;
20:2^2*5^1;

排列组合这里需要自己理解一下。

求数N的所有因子之和

             根据算术基本原理：

              根据积性函数：

 

等价的式子：

解释这个式子：其实如果理解了上面的那个N因子的个数的原理这个也就比较容易理解了（看第二个式子吧，第二个比较好理解）

看第二个式子：原理也是排列组合用一个例子来说明吧：

1 :2^0*5^0;
5 :2^0*5^1;
2 :2^1*5^0;
10:2^1*5^1;
4 :2^2*5^0;
20:2^2*5^1;
因子数的和：(2^0+2^1+2^2)*(5^0+5^1)=(1+2+4)*(1+5)= 1*1 + 1*5 + 2*1 + 2*5 + 2^2*1 + 2^2*5;

      1*1=1
	  1*5=5
	  2*1=2
	  2*5=10
	  2^2*1=4
	  2^2*5=20
	（1,5,2,10,4,20）为因子，然后和就是 1*1 + 1*5 + 2*1 + 2*5 + 2^2*1 + 2^2*5 

按照式子理解：

就是说把这些质因子所得到的所有的因子的和加起来。

从算术基本原理来考虑GCD和LCM   

当然这也可以扩展到求N个数的GCD和LCM