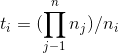数论算法总结
目录
一.欧拉函数
二.指数循环节
三.欧拉定理（费马小定理）
四.二次探测定理
五.威尔逊定理
六.Miller-Rabin素性测试
七.二元一次不定方程
1.结论及证明
2.扩张欧几里得
八．乘法逆元
九.拉格朗日插值法
十.中国剩余定理（CRT）
1.引入
2.证明及结论
十一.高斯消元
十二.组合数
1.公式
2.杨辉三角
2.预处理阶乘法
十三.容斥原理
谢谢
一.欧拉函数
浅显易懂地理解，欧拉函数
就是求比n小，且与n互质的数的个数。如
，因为1,2与3互质。这个函数十分有用，一定要记住。它的求法是：
附代码：
int res = n;
for (int i = 2; i * i <= n; i ++){
if (n % i == 0){
res = res / i * (i - 1);
while (n % i == 0)
n /= i;
}
}
if (n > 1)
res = res / n * (n - 1);二.指数循环节
这个指数循环节主要用于降幂，让你的快速幂变得更快，公式如下：
一定要注意后面的条件：b>=phi（p）！
对于long long范围内的b就这样求就行了，但对于大整数b要这样求：
char B[100];
int mod;
scanf ("%s %d", B, &mod);
int len = strlen (B);
int b = 0;
for (int i = 0; i < len; i ++)
b = (b * 10 + B[i] - 48) % phi (mod);//位数从高到低，b是最终的指数，mod是模数如果有兴趣，我有一道对于提升指数循环节的题目：Calculation
三.欧拉定理（费马小定理）
先给出定理：
欧拉定理：
(mod p) （a,p互质） 费马小定理：
(mod p) （p为质数）
显然，费马小定理就是欧拉定理的特殊情况，所以，我们只用来证明欧拉定理：
证明：
设p的缩系为：
，
则有：
(mod p)
再把同余式左右两边一约，就得出定理(mod p)
四.二次探测定理
二次探测定理：
当且仅当p是奇素数时。
五.威尔逊定理
威尔逊定理：
等同于
（p为素数）
六.Miller-Rabin素性测试
说白了，就是迅速地判断质数，运用二次探测定理和费马小定理判断素数。错误率非常低。
证明：
1.若?是奇数，找到最大的?使得?−1=2??若n是奇数，找到最大的k使得n-1=2^k m
2.随机取一小于?n的整数?a，计算?=??x=a^m
3.若?2≡1??? ?而?≠1且?≠?−1x^2≡1(mod n)而x≠1且x≠n-1，那么?n一定不是素数，算法结束。否则令?=?2%?x=x^2%n，重新回到步骤3。步骤3一共执行?次k次。
4.现在?x的值为??−1%?a^(n-1)%n，若?≠1x≠1，则?a关于?n不满足费马小定理，?n一定不是素数，算法结束。
5.若算法没有结束，则称?n通过了一轮素性测试，? n 很有可能是素数，误判率在1/4以内。此时可选择回到步骤2，进行多轮素性测试，误判率将指数级收敛。
模板：
inline LL mul (LL a, LL b, LL mod){//快速模
LL res = 0;
for ( ; b; a = (a + a) % mod, b /= 2)
if (b & 1)
res = (res + a) % mod;
return res;
}
inline LL qkpow (LL a, LL n, LL mod){//快速幂
LL res = 1;
for ( ; n; a = mul (a, a, mod), n /= 2)
if (n & 1)
res = mul (res, a, mod);
return res;
}
inline bool Miller_Rabin (LL n){
if (n == 2 || n == 3 || n == 5 || n == 7)
return 1;
if (!(n % 2) || !(n % 3) || !(n % 5) || !(n % 7))
return 0;
LL m = n - 1, k = 0;
while (!(m & 1)){
k ++;
m /= 2;
}
for (register LL i = 1; i <= 5; i ++){
LL a = rand () % (n - 1) + 1, x = qkpow (a, m, n), y;//随机选数来判断
for (register LL j = 1; j <= k; j ++){
y = mul (x, x, n);
if (y == 1 && x != 1 && x != n - 1)
return 0;
x = y;
}
if (y != 1)
return 0;
}
return 1;
}有一道需要用到威尔逊定理和Miller-Rabin素性测试的题目，十分巧妙，可以尝试一下：Zball in Tina Town
七.二元一次不定方程
1.结论及证明
当且仅当gcd(a,b)|c是有整数解。
2.扩张欧几里得
这是用于解一般二元一次不等式：
(a,b互质)。
模板：
int exgcd (int a, int b, int &x, int &y){
if (！b){
x = 1, y = 0;
return a;
}
int r = exgcd (b, b % a，y，x)；
y -= x * (a / b);
return r;
}八．乘法逆元
乘法逆元：b的逆元为：
，有
逆元求法：
九.拉格朗日插值法
本人实在不了解，推荐博客：
点击打开链接
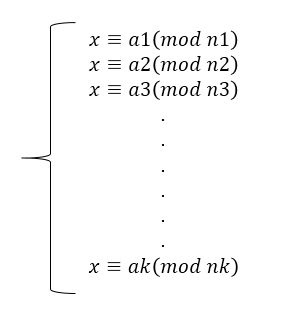
十.中国剩余定理（CRT）
1.引入
有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？——《孙子算经》
古代数学家给出了解决这个问题的口诀：三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五便得知
由于2是5*7=35关于3的逆元，1是3*7=21关于5的逆元，1是3*5关于7的逆元
“七十”=2*35，“廿一”=1*21，“正半月”=1*15，“百零五”=3*5*7
所以通解即为(2*70+3*21+2*15)+105k
最小的正整数解为23
2.证明及结论
中国剩余定理就是解形如：
的方程组。
先找一个数
使得
由方程二可知：
其中
于是，其中的一组特结为：
通解为：
附代码：
//b[i]是模数，p[i]是同于是右边的ai，M是所有模数的公倍数
void exgcd (int a, int b, int &x, int &y){
if (! b){
x = 1;
y = 0;
return ;
}
exgcd (b, a % b, y, x);
y -= a / b * x;
}
int main (){
int ans = 0;
int x, y;
for (int i = 1; i <= 3; i ++){
int tp = M / b[i];
exgcd (tp, b[i], x, y);
ans = (ans + p[i] * tp * x) % M;
}十一.高斯消元
就是一种高级的消元，时间复杂度
。
算法流程：枚举每一列和每一行i，每次枚举将第i行的第i列保留，将第i列上的其他数全部消为零，最后剩下的就是每一项未知数的解。
要注意各种特殊情况，比如无解和多解。
核心代码
void gauss (){
int num = 1;
for (int i = 1; i <= n; i ++){
int j;
for (j = num; ! a[j][num] && j <= n; j ++);
for (int k = 1; k <= n + 1; k ++) swap (a[j][k], a[num][k]);
for (int k = n; k >= now; k --) f[now][k] /= f[now][now];
for (int j = 1; j <= n; j ++){
if (j != num){
double t = a[j][num] / a[num][num];
for (int k = 1; k <= n + 1; k ++)
a[j][k] -= t * a[num][k];
}
}
num ++;
}
}十二.组合数
1.公式
组合C，大家都知道吧：
朴素算法:
if (k > n / 2)
k = n - k;
for (int i = k; i >= 1; i --)
ans = ans * (n - i + 1) / (k - i + 1);2.杨辉三角
杨辉三角是预处理组合数的一种办法，它的递推式是：
但是其储存的空间狭窄，又有预处理阶乘法：
2.预处理阶乘法
就是预处理出每个数的逆元和阶乘，以便计算组合数：
int fac[105], rfac[105];//fac[i]是阶乘，rfac[i]是逆元
void prepare (int x){
fac[1] = fac[0] = rfac[1] = rfac[1];
for (int i = 2; i <= x; i ++){
fac[i] = 1ll * fac[i - 1] * i % mod;
rfac[i] = 1ll * rfac[x % i] * (x - x / i) % mod;
}
for (int i = 2; i <= x; i ++)
rfac[i] = 1ll * rfac[i - 1] * rfac[i] % mod;
}
int C (int n, int k){
if (k > n)
return 0;
return fac[n] * rfac[k] % mod * rfac[n - k] % mod;
}
十三.容斥原理
容斥原理就是人们找出的一种对于某些有重叠部分的元素，不重不漏的计算方法。
这有很多经典例题，待我写后就粘上来。这些题有：
1.两双手
2.表达式计数
3.Bar Codes
4.集合计数
5.放棋子