【CF888G】 Xor-MST 简易题解
题目大意
\ \ \ \ \ \ \, 给你一个 n n n 个节点的完全图,第 i i i 个点的权值为 a i a_i ai ,两点的之间边权为这两个点权值的异或值,求最小生成树的权值。
想法
\ \ \ \ \ \ \, 其实这道题没有那么复杂,还是好想的。
\ \ \ \ \ \ \, 最小生成树的话,我们显然有一个基于贪心的 K r u s k a l Kruskal Kruskal 算法,复杂度 O ( n 2 log n ) O(n^2\log n) O(n2logn),想想还是算了吧。
\ \ \ \ \ \ \, 而遇到关于异或的题呢,我们一般会有两种想法:整形异或线性基, T r i e Trie Trie 树。
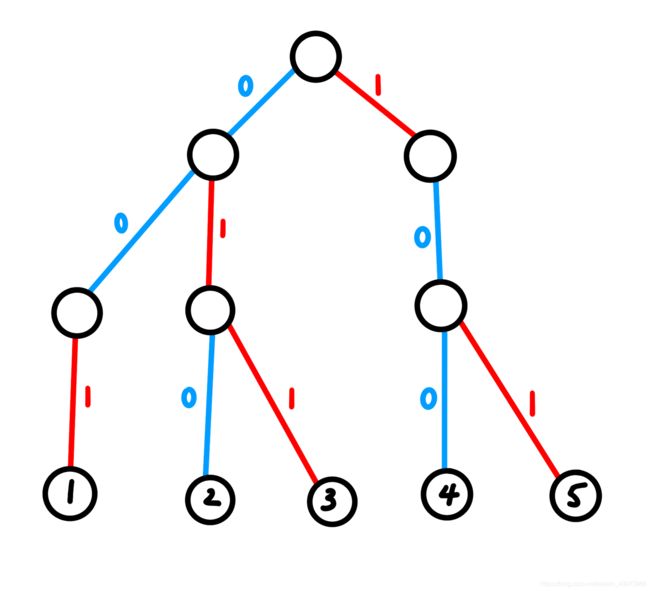
\ \ \ \ \ \ \, 容易想到的,这道题当然和线性基没有关系了,我们思考一下 T r i e Trie Trie 树,首先,我们先把第一个样例从高位到低位插入线性基看看:
\ \ \ \ \ \ \, 容易发现,对于每个叶子节点,既每个点值之间,要是需要互相连边,那么求 他们 L c a Lca Lca 以后的边的亦或值 即可。
\ \ \ \ \ \ \, 由此可得,若是 L c a Lca Lca 的深度越深,便约优。因为我们是从高位到低位插入的,所以浅的点权值较大,要尽量避免选择浅的点。
\ \ \ \ \ \ \, 我们不妨把可能是 L c a Lca Lca 的点拉出来瞅瞅:
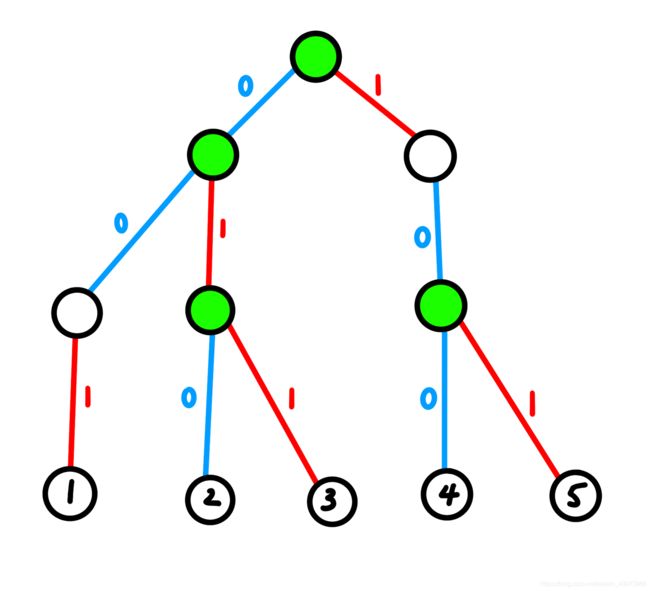
\ \ \ \ \ \ \, 惊喜地发现,刚好有 4 4 4 个点,也就是所有拥有两个儿子的点一共有 4 4 4 个,可以证明,如果 a i a_i ai 两两不等的话,那么这种点一共有 n − 1 n-1 n−1 个,那么答案就呼之欲出了:
\ \ \ \ \ \ \, 我们每找到这样的点,就暴力贪心 D F S DFS DFS 下去:
- 每次尽量同时走左儿子或右儿子;
- 如果两个都有,就两个都走,然后返回值取 m i n min min 。
- 如果两个只有不一样的儿子,就在返回值加上这一深度 b i t bit bit的值,然后继续走
\ \ \ \ \ \ \, 最终答案就是他们的 D F S DFS DFS 值的和。
\ \ \ \ \ \ \, 那如果 a i a_i ai 不是两两不等的话怎么办呢,如果 a u = a v a_u=a_v au=av 的话,我们当然首先建一条边连接 u u u, v v v,权值为 0 0 0,对答案完全没有影响,所以我们正常建,正常搜,是不会有问题的。
#include