OpenJudge2704 寻找平面上的极大点(重庆一中高2018级信息学竞赛测验9) 解题报告
【问题描述】
给定n个点的集合,一定存在若干个点,它们不会被集合中的任何一点所支配,这些点叫做极大值点。请编程找出所有的极大点,按照x坐标由小到大,输出极大点的坐标。
【输入格式】
输入包括两行,第一行是正整数n,表示是点数,第二行包含n个点的坐标,坐标值都是整数,坐标范围从0到100,输入数据中不存在坐标相同的点。
【输出格式】
按x轴坐标最小到大的顺序输出所有极大点。输出格式为:(x1,y1),(x2,y2),...(xk,yk),按x由小到大,x相同则按y由小到达输出。注意:输出的每个点之间有","分隔,最后一个点之后没有",",少输出和多输出都会被判。
【输入样例】
5
1 2
2 2
3 1
2 3
1 4
【输出样例】
(1,4),(2,3),(3,1)
【样例解释】
样例的点和极大点的图形如下:
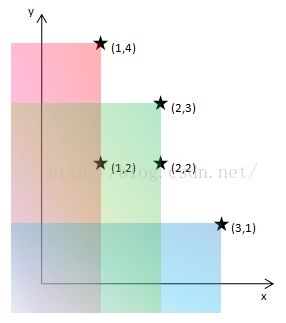
【数据范围】
80%的数据满足:n<=6000
100%的数据满足:n<=100000
考后反思:话说这道题是考试时的第一道题,一般都是比较简单的,所以不要想得太复杂了。
在一个平面上,如果有两个点(x,y),(a,b),如果说(x,y)支配了(a,b),这是指x>=a,y>=b;用图形来看就是(a,b)坐落在以(x,y)为右上角的一个无限的区域内。
给定n个点的集合,一定存在若干个点,它们不会被集合中的任何一点所支配,这些点叫做极大值点。请编程找出所有的极大点,按照x坐标由小到大,输出极大点的坐标。
【输入格式】
输入包括两行,第一行是正整数n,表示是点数,第二行包含n个点的坐标,坐标值都是整数,坐标范围从0到100,输入数据中不存在坐标相同的点。
【输出格式】
按x轴坐标最小到大的顺序输出所有极大点。输出格式为:(x1,y1),(x2,y2),...(xk,yk),按x由小到大,x相同则按y由小到达输出。注意:输出的每个点之间有","分隔,最后一个点之后没有",",少输出和多输出都会被判。
【输入样例】
5
1 2
2 2
3 1
2 3
1 4
【输出样例】
(1,4),(2,3),(3,1)
【样例解释】
样例的点和极大点的图形如下:

【数据范围】
80%的数据满足:n<=6000
100%的数据满足:n<=100000
做题思路(错解):考试拿到这道题时,感觉非常熟悉,因为之前在OpenJudge上做过这道题,然而因为做题的时间离现在有点久,再加上当时做这道题时做得有点复杂,所以在想题时思路比较局限,想了一种比较复杂的解法,但最后因为小的细节导致错误。
解题思路(正解):根据题意,极大点即为在自己右上方(包括正右和正上方)没有其它点的点,最简单的思路就是直接暴力枚举每个点,判断它的右上方是否有其它点,如果没有则该点即为极大点,这种算法的时间复杂度为O(n^2),对于n=100000的数据显然会超时。
其实根据极大点的定义和样例解释的图,我们不难发现在x由小到大有序排列时,极大点的y是严格递减的,所以我们可以先将输入的点按x由小到大排序(x相等时,按y由小到大排序),因为x最大且y最大的点(即排序后的最后一个点)一定是极大点,所以可以从第N个点开始倒着枚举每个点,设maxy来记录当前极大点中y的最大值,当第i个点的y大于maxy时,该点就是极大点。对于极大点的记录可以用vis数组进行标记,或者将极大点存在一个结构体中,找完极大点后将该结构体按题目要求的顺序排序,然后输出即可,此算法的时间复杂度为O(n)。
#include
#include
#include
#include
#include
using namespace std;
const int maxn=100005;
int N;
struct data
{
int x,y;
};
data a[maxn],ans[maxn];
bool cmp1(data aa,data bb)
{
if(aa.x!=bb.x) return aa.x=0;i--)
{
if(a[i].y>maxy) //严格递增
{
cnt++;
ans[cnt].x=a[i].x,ans[cnt].y=a[i].y;
maxy=a[i].y;
}
}
sort(ans+1,ans+1+cnt,cmp1);
printf("(%d,%d)",ans[1].x,ans[1].y); //注意输出是不能多输','
for(int i=2;i<=cnt;i++)
printf(",(%d,%d)",ans[i].x,ans[i].y);
return 0;
} 考后反思:话说这道题是考试时的第一道题,一般都是比较简单的,所以不要想得太复杂了。
