UVA1625 颜色的长度（color length）（重庆一中高2018级信息学竞赛测验10） 解题报告

【问题描述】  
  
　　输入两个颜色序列（只包含大写字母的字符串），要求按顺序合并成同一个序列，即每次可以把一个序列的开头的颜色放到新序列的尾部。 

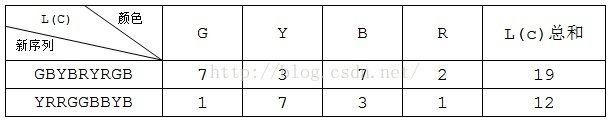
　　例如，两个颜色序列GBBY和YRRGB，至少有两种合并结果：GBYBRYRGB和YRRGGBBYB。对于每个颜色c来说，其跨度L(c)等于最大位置和最小位置之差，例如对于上面两种合并结果，每个颜色的L(c)和所有L(C)总和如下表： 

　　　　 
　　你的任务是找一种合并方式，使得所有L(c)的总和最小。
 
    
 【输入格式】  
  
　　输入包含两行，每行一个只含大写字母的字符串，表示两个颜色序列。（注意，UVA题库上该题为输入T组数据）
 
    
 【输出格式】  
   
　　输出一个整数，表示L(c)总和的最小值。（UVA题库上，对于每组输入数据，输出一个整数）
 
    
 【输入样例】   
   
【样例1】
　AAABBCY
　ABBBCDEEY


【样例2】
　GBBY
　YRRGB


 
    
 【输出样例】  
   
【样例1】
　10


【样例2】
　12 
 
    
 【数据范围】  
   
颜色序列的长度不超过5000。
 
    
 【来源】  
  
《算法竞赛》276页，UVa1625

做题思路（错解）：拿到这道题时， 因为要求L(c)的总和的最小值，首先想到的就是动态规划，设状态函数f(i,j)表示选择s1的前i个字符和s2的前j个字符L(c)总和的最小值，虽然函数设对了，但在分析状态转移方程时卡住了，于是在考试时推出了错误并且复杂的状态转移方程。

解题思路（正解）：根据题意，问什么设什么，设状态函数f(i,j)表示选择s1的前i个字符和s2的前j个字符L(c)总和的最小值，分析f(i,j)时，可以选择s1的第i个字符，也可以选择s2的第j个字符，但其实如果要每次计算L(c)是很麻烦的，因为我们只关心最后的答案，即选择s1的所有字符和s2的所有字符的L(c)的总和，所以可以设g[i][j]表示取了s1的前i个字符和s2的前j个字符后剩余字符中颜色已经出现但尚未结束的个数，则状态转移方程为f(i,j)=min{f(i-1,j),f(i,j-1)}+g[i][j]，边界条件为f(0,0)=0。

接下来就是预处理计算g[i][j]，为了知道每种颜色是否出现结束，可以用数组来记录每种颜色的出现的起始位置和结束位置，则计算g[i][j]时可以直接枚举每种颜色，如果这种颜色在两个序列中任意一个序列的该颜色的起始位置上或后，并且在任意一个序列的该颜色的结束位置前，g[i][j]就要+1。

需要注意的是，该题颜色序列的长度最多为5000，如果使用两个二维数组会超内存，所以在进行动态规划时，要使用滚动数组。

（该题的思路较难，如果有不懂的，建议看一下《算法竞赛》276页对于该题的分析）

注：这里附上的代码是交UVA的代码，与考试题的输入输出要求稍有差别

#include
#include
#include
#include
#include
using namespace std;
const int maxn=5005;
const int inf=2000000010;
int N,M,T;
char s[maxn],ss[maxn];
int s1[30],s2[30],e1[30],e2[30],g[maxn][maxn];  //g[i][j]表示取了s1的前i个字符和s2的前j个字符后剩余字符中颜色已经出现但尚未结束的个数
/*
f(i,j)表示选择s1的前i个字符和s2的前j个字符L(c)总和的最小值
f(i,j)=min{f(i-1,j),f(i,j-1)}+g[i][j]
边界：f(0,0)=0 
*/
int d[2][maxn];  //注意使用滚动数组
void solve()  //动态规划
{
	for(int i=0;i<=N;i++)
	for(int j=0;j<=M;j++)
	d[i%2][j]=inf;
	d[0][0]=0;
	for(int i=0;i<=N;i++)
	for(int j=0;j<=M;j++)
	{
		if(i==0 && j==0)  continue;
		int t1=inf,t2=inf;
		if(i-1>=0)  t1=d[(i-1)%2][j];
		if(j-1>=0)  t2=d[i%2][j-1];
		d[i%2][j]=min(t1,t2)+g[i][j];
	}
	printf("%d\n",d[N%2][M]);
}
int main()
{
	//freopen("48.in","r",stdin);
	//freopen("48.out","w",stdout);
	scanf("%d",&T);
	while(T--)
	{
	scanf("%s",s+1);
	scanf("%s",ss+1);
	N=strlen(s+1),M=strlen(ss+1);
	memset(s1,100,sizeof(s1));
	memset(s2,100,sizeof(s2));
	memset(e1,0,sizeof(e1));
	memset(e2,0,sizeof(e2));
	for(int i=1;i<=N;i++)
	{
		s1[s[i]-'A']=min(s1[s[i]-'A'],i);  //记录第一个序列中每种颜色出现的起始位置
		e1[s[i]-'A']=i;  //记录第一个序列中每种颜色出现的结束位置
	}
	for(int i=1;i<=M;i++)
	{
		s2[ss[i]-'A']=min(s2[ss[i]-'A'],i);  //记录第二个序列中每种颜色出现的起始位置
		e2[ss[i]-'A']=i;  //记录第二个序列中每种颜色出现的结束位置
	}
	for(int i=0;i<=N;i++)
	for(int j=0;j<=M;j++)
	{
		int t=0;
		for(int k=0;k<26;k++)  //枚举每种颜色
		{
			if((s1[k]<=i || s2[k]<=j) && (e1[k]>i || e2[k]>j))  t++;
		}
		g[i][j]=t;
	}
	solve();
	}
	/*for(int i=0;i<=N;i++)
	{
		for(int j=0;j<=M;j++)
		printf("%d ",g[i][j]);
		printf("\n");
	}*/
	return 0;
}