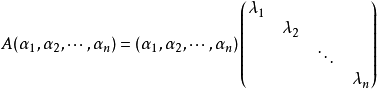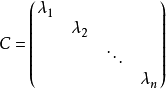【几种特殊的矩阵:对角矩阵、上下三角矩阵、正态分布随机矩阵、魔方矩阵、希尔伯特矩阵、托普利兹矩阵】

（这两个最不特殊了，线代中学过不过有点忘）
1、对角矩阵：
      对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag（a1，a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种，值得一提的是：对角线上的元素可以为 0 或其他值，对角线上元素相等的对角矩阵称为数量矩阵；对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算，且结果仍为对角阵。
两个运算规则：i.数与对角阵的乘积仍为对角阵。
ii.同阶对角矩阵的乘积仍为对角阵，且它们的乘积是可交换的：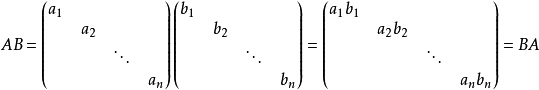

n阶矩阵A相似于对角矩阵的充要条件是A有n个线性无关的特征向量：
若n阶矩阵A有n个不同的特征值，则A必能相似于对角矩阵。
说明：当A的特征方程有重根时．就不一定有n个线性无关的特征向量，从而未必能对角化。
证明过程：
（1）必要性。设有可逆矩阵P，使得
                                                                

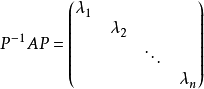
令矩阵P的n个列向量为  ，则有

                           

因而  ，因为P为可逆矩阵，所以   为线性无关的非零向量，它们分别是矩阵A对应于特征值

  的特征向量。
（2）充分性。
由必要性的证明可见，如果矩阵A有n个线性无关的特征向量，设它们为   ，对应的特征值分别为  ，则有  ，以这些向量为列构造矩阵  ，则P可逆，且，其中C为：

                                                                         

    即  。
2、上下三角矩阵：
主对角线以下都是零的方阵称为上三角矩阵。上三角矩阵具有行列式为对角线元素相乘、上三角矩阵乘以系数后也是上三角矩阵、上三角矩阵间的加减法和乘法运算的结果仍是上三角矩阵等性质。
i、  上三角矩阵的行列式为对角线元素相乘；
ii、 上三角矩阵乘以系数后也是上三角矩阵；
iii、 上三角矩阵间的加减法和乘法运算的结果仍是上三角矩阵；
iiii、上三角矩阵的逆矩阵也仍然是上三角矩阵。
严格上(下)三角矩阵：若上（下）三角矩阵对角线元素全是1，则称为严格上（下）三角矩阵。
初次见：
3、正态分布随机矩阵
（例3-23）
4、魔方矩阵：魔方矩阵又称幻方，有相同的行数和列数，并在每行每列、对角线上的和都相等的矩阵。魔方矩阵中的每个元素不能相同。能构造任何大小（除了2x2）的魔方矩阵。
每行、每列及对角线之和被称为魔术常量或魔法总和M。

                                                                                                n为阶数。

 最简单的魔方就是平面魔方，还有立体魔方、高次魔方等。
平面魔方的定义：将自然数 1 到 N^2， 排列 N 行 N 列的方阵，使每行、每列及两条主对角线上的 N 个数的和都等于N (N^2+1)/2，这样的方阵称为 N 阶幻方。
构造方法：
         分为三种情况：N为奇数、N为4的倍数、N为其它偶数(4n+2的形式)

N 为奇数时
(1) 将1放在第一行中间一列;
(2) 从2开始直到n×n止各数依次按下列规则存放：
      按 45°方向行走，如向右上
     每一个数存放的行比前一个数的行数减1，列数加1
(3) 如果行列范围超出矩阵范围，则回绕。
      例如1在第1行，则2应放在最下一行，列数同样加1;
(4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时，
     则把下一个数放在上一个数的下面。
构造一个三阶魔方：

8	1	6
3	5	7
4	9	2

 

N为4的倍数时 
采用对称元素交换法。    
首先把数1到n×n按从上至下，从左到右顺序填入矩阵
然后将方阵的所有4×4子方阵中的两对角线上的数关于大方阵中心作中心对称交换（注意是各4×4子方阵对角线上的数）， 即a(i,j)与a(n+1-i,n+1-j)交换，所有其它位置上的数不变。(或者将对角线不变，其它位置对称交换也可)
N 为其它偶数时
当n为非4倍数的偶数(即4n+2形)时：首先把大方阵分解为4个奇数(2m+1阶)子方阵。
按上述奇数阶魔方给分解的4个子方阵对应赋值
上左子阵最小(i)，下右子阵次小(i+v)，下左子阵最大(i+3v)，上右子阵次大(i+2v)
即4个子方阵对应元素相差v，其中v=n*n/4
四个子矩阵由小到大排列方式为 ① ③ ④ ②
然后作相应的元素交换：a(i,j)与a(i+u,j)在同一列做对应交换(jn-t+2),
注意其中j可以取零。
a(t-1,0)与a(t+u-1,0)；a(t-1,t-1)与a(t+u-1,t-1)两对元素交换
其中u=n/2，t=(n+2)/4 上述交换使每行每列与两对角线上元素之和相等。
Matlab中自动生成魔方矩阵的函数:   magic(n) n是矩阵维数

// 交换
void Exchange(int **pj, int tr, int tc, int n) {
    n++;
    if (1 <= tr && tr <= n / 2 && 1 <= tc && tc <= n) {
        pj[tr][tc] += pj[n - tr][n - tc];
        pj[n - tr][n - tc] = pj[tr][tc] - pj[n - tr][n - tc];
        pj[tr][tc] -= pj[n - tr][n - tc];
    }
}
int main(){
    int n, i = 0, j = 0, **pj;
    int tr, tc;
    printf("输入魔方矩阵的阶层：");
        scanf("%d",&n);
    // 初始化二维数组
    pj = (int**)malloc(sizeof(int **) * (n + 1));
    for (i = 0; i < (n + 1); i++)
        pj[i] = (int*)malloc(sizeof(int *) *  (n + 1));

    // n为奇数时
    if (n % 2 == 1) {
        // 1.将1放至第一行中间
        i = 1; j = n / 2 + 1;
        pj[1][n / 2 + 1] = 1;

        // 2.沿右上45°，依次放置剩下的数
        for (int k = 2; k <= n * n; k++) {
            // 行数上移，列数右移，即右上45°移动
            tr = i - 1; tc = j + 1;

            // 条件一：若超出，则回绕
            if (tr < 1) tr = n;
            if (tc > n) tc = 1;
            // 条件二：若有数据，则放在上一个数字之下
            if (0 < pj[tr][tc] && pj[tr][tc] <= n * n) {
                tr = i + 1; tc = j;
                if (tr < 0) tr = n;
            }
            pj[tr][tc] = k;
            i = tr; j = tc;
        }

    }
    // n为4的倍数时
    else if (n % 4 == 0) {
        i = 1; j = 1;

        // 1.先将数据从上到下，从左到右填入
        for (int k = 1; k <= n * n; k++) {
            pj[i][j++] = k;
            if (j > n) { j = 1; i++; }
        }

        // 2.将方阵的所有4*4子方阵中的两对角线上的数
        // 关于大方阵中心作中心对称交换

        i = 1; j = 1;
        for (size_t r = 0; r < n / 4 + 1; r++) {
            for (size_t c = 0; c < n / 4 + !(r % 2); c++) {
                tr = 2 * r + i;
                tc = 4 * c + r % 2 * 2 + j;

                Exchange(pj, tr, tc, n);
                Exchange(pj, tr - 1, tc, n);
                Exchange(pj, tr, tc - 1, n);
                Exchange(pj, tr - 1, tc - 1, n);
            }
        }

    }
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++)
            printf("%d\t", pj[i][j]);
        printf("\n");
    }
}

Hilbert 矩阵 ：矩阵的一种，其元素H（i,j）=1/(i+j-1)，i,j分别为其行标和列标。
                     5阶的：
                         

希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态（即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化），病态程度和阶数相关。Matlab中生成希尔伯特矩阵的函数是hilb(n)；求希尔伯特矩阵的逆的函数是invhilb(n)，其功能是求n阶的希尔伯特矩阵的逆矩阵。（使用一般方法求逆会因为原始数据的微小扰动而产生不可靠的计算结果。）
Toeplitz 矩阵 ：
托普利兹矩阵的主对角线上的元素相等，平行于主对角线的线上的元素也相等；矩阵中的各元素关于次对角线对称，即T型矩阵为次对称矩阵。简单的T形矩阵包括前向位移矩阵和后向位移矩阵。在数学软件Matlab中，生成托普利兹矩阵的函数是：toeplitz(x,y)。它生成一个以 x 为第一列，y 为第一行的托普利兹矩阵，这里x, y均为向量，两者不必等长。
设  ，如果 ，即：

                                                             

则称  为托普利兹矩阵（Toeplitz matrix）
（1）托普利兹矩阵完全由其第1行和第1列的2n一1个元素确定。
（2）托普利兹矩阵沿平行主对角线的每一对角线上的元素是相等的，是关于交叉对角线对称的。显然，有：  ，其中            为反向单位矩阵 
（3）除第一行第一列外，其他每个元素都与左上角的元素相同。 
（4）矩阵中的各元素关于次对角线对称，即T型矩阵为次对称矩阵。
这个托普利兹矩阵的这几个性质有些看了百科...不懂  百科