计算机图形学中点分割算法法 (线段与矩形关系的判断 向量)

线段与矩形的关系我理解的是三种：

1、线段完全在矩形内
2、线段完全在矩形外
3、线段有一部分在矩形内
点与矩形的关系比线段与矩形的关系更容易判断，所以以下都是通过端点的情况去判断线段与矩形的关系的。具体也是分为三种：
1、线段两端点都在矩形内
2、线段一个端点在矩形内一个在矩形外
3、线段两个端点都在矩形外

1、线段两端点都在矩形内：

　　很容易得出这种情况下，线段是完全在矩形内部的。具体关系可以根据线段端点与矩形四个顶点的来判断，我就不细说了。

2、线段一个端点在矩形内一个在矩形外

　　这种情况，线段有一部分在矩形内部，端点判断与情况1一样，也很容易得出。
　　这里额外说一下这种情况下求线段与矩形的交点，可以用中点分割法：思路就是二分。贴一下图更容易懂。
　　
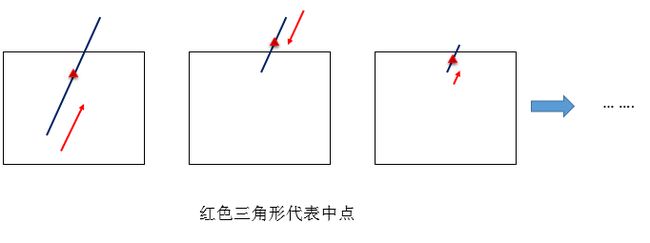
　　过程：当中点在矩形内部时，内部端点移向中点；当中点在矩形外部时，外部端点移向中点，直到中点与内部端点相等或者中点与外部端点相等。

3、线段两个端点都在矩形外

　　这个是分析的重点，因为两个端点都在矩形外，线段与矩形的关系不止一种情况。可能线段完全在矩形外，可能线段有一部分在矩形内部。

　　这时候需要通过线段是否与矩形的对角线是否相交，来区分这两种情况。如果与对角线没有交点，则线段完全在矩形外部，反之有一部分在矩形内部。
　　这时候问题就转化成了求两条线段是否相交。因为两条线段的端点都是知道的，最容易想到的就是通过求解直线方程，通过有无交点来判断两线段是否相交。
　　但是这里我给大家详细解说一下如何用向量方法去判断两线段是否相交，并且求交点。

向量方法判断两线段是否相交，并求出交点

　　如果两向量相交，则两向量肯定相互跨立。向量的跨立是什么意思呢？

　　如图有向量(p1-p2)和向量(Q2-Q1),如果跨立，则点Q1，点Q2在肯定在直线P1P2的两侧，意思就是向量(Q2-P1),(Q1-P1)在向量(P2-P1)的两侧。由向量的向量积(不懂可以看 向量的点乘与叉乘的几何意义）可以判断向量(Q2-P1),(Q1-P1)是不是在向量(P2-P1)的两侧(^代表叉乘)：若d1 = (P2-P1)^(Q2-P1) * (P2-P1)^(Q1-P1) < 0代表异侧，否则>0代表同侧。
　　同理，还要判断一次向量(P1-Q1),(P2-Q1)是不是在向量(Q2-Q1)两侧

即若d2 = (Q2-Q1)^(P2-Q1) * (Q2-Q1)^(P1-Q1) < 0代表异侧，否则>0代表同侧。
当d1 < 0 && d2 < 0,两线段相交，否则不相交。
上述过程也称为跨立实验，如果觉得我说得不好，大家可以网上百度下。
当然我们还要考虑两条线段重合的情况，也就是d1 == 0,d2 == 0的情况，这两种也代表了线段有一部分在矩形内部。
所以综上所述，当d1 <= 0 && d2 <= 0时，线段部分在矩形内，否则完全在矩形外。
到这里已经把线段与矩形的关系完全判断出来了。
　　这里额外说一下，第三种情况下(两端点都在矩形外部)确定线段与矩形对角线有交点后如何不通过求直线方程来获得交点。已知线段两端点(p1x,p1y),(p2x,p2y),对角线两端点(q1x,q1y),(q2x,q2y)，设交点为(x,y),则存在t,s,使
x = p1x + t * (p2x - p1x); —1
y = p1y + t * (p2y - p1y); —2
x = q1x + s * (q2x - q1x); —3
y = q1y + s * (q2y - q1y); —4
由1，3得
t * (p2x-p1x) - s * (q2x - q1x) = q1x - p1x; —5
由2，4得
t * (p2y-p1y) - s * (q2y - q1y) = q1y - p1y; —6
联立5，6得
t = [(q1x-p1x)(q2y-q1y)-(q1y-p1y)(q2x-q1x)] / [(p2x-p1x)(q2y-q1y)-(p2y-p1y)(q2x-q1x)]
可以观察得出分母就是向量(P2-P1)与向量(Q2-Q1)的向量积的模。t和s求一个就好了。之后根据
x = p1x + t * (p2x - p1x); —1
y = p1y + t * (p2y - p1y); —2
来求得交点坐标。找到交点之后，可以把点段当做两条，根据折半查找来确定线段与矩形的两个交点。

代码

以下是从裁剪框裁剪线的程序中截出来的部分，有些变量不懂耶不用管。对算法是实现没有影响。

//判断线段端点与矩形顶点的关系
bool judgePointInnerOrOuter(CPoint p,CPoint m_window[2])
{
    int minx,miny,maxx,maxy;
    minx = m_window[0].x>m_window[1].x ? m_window[1].x : m_window[0].x;
    maxx = m_window[0].x<=m_window[1].x ? m_window[1].x : m_window[0].x;
    miny = m_window[0].y>m_window[1].y ? m_window[1].y : m_window[0].y;
    maxy = m_window[0].y<=m_window[1].y ? m_window[1].y : m_window[0].y;

    if(p.x.x>maxx||p.y.y>maxy)
        return false;
    else
        return true;
}

//折半找交点
CPoint bSearch(CPoint out,CPoint inn,CPoint m_window[2])
{
    CPoint mid;
    bool code;
    int d1,d2;
    d1 = inn.x-out.x;
    d2 = inn.y-out.y;
    mid.x = out.x + d1/2;
    mid.y = out.y + d2/2;
    while(abs(out.x-inn.x)>1||abs(out.y-inn.y)>1){
        code = judgePointInnerOrOuter(mid,m_window);
        if(code)    inn = mid;
        else        out = mid;
        d1 = inn.x-out.x;
        d2 = inn.y-out.y;
        mid.x = out.x + d1/2;
        mid.y = out.y + d2/2;
    }
    return inn;
}

//向量法判断两个线段的位置关系
bool judgeLineToLine(CPoint a,CPoint b,CPoint c,CPoint d)
{
    long long int d1,d2,d3,d4;
    //1 = b-a  2 = c-a
    d1 = (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
    //1 = b-a  2 = d-a
    d2 = (b.x-a.x)*(d.y-a.y)-(b.y-a.y)*(d.x-a.x);
    //1 = d-c  2 = a-c
    d3 = (d.x-c.x)*(a.y-c.y)-(d.y-c.y)*(a.x-c.x);
    //1 = d-c  2 = b-c
    d4 = (d.x-c.x)*(b.y-c.y)-(d.y-c.y)*(b.x-c.x);
    if(d1*d2<=0&&d3*d4<=0)
        return true;//相交及重合
    else 
        return false;//不相交
}

//得到线段与对角线的交点
CPoint getPoint(CPoint out1,CPoint out2,CPoint point1,CPoint point11)
{
    int a = out2.x-out1.x;
    int b = point1.x-point11.x;
    int c = out2.y-out1.y;
    int d = point1.y-point11.y;
    int g = point1.x-out1.x;
    int h = point1.y-out1.y;
    int f = a*d-b*c;
    double t = double((d*g-b*h))/double(f);
    CPoint m;
    m.x = out1.x+t*(out2.x-out1.x);
    m.y = out1.y+t*(out2.y-out1.y);
    return m;
}

//中点分割法求线段与矩形的关系以及交点
void MyClip::midpointSubdivisionAlgorithm()
{
    if(!myWindowDefined && !myLineDefined)  return;//这个不用管
    CPoint p1, p2;
    p1 = m_ClippingLine[0];//线段端点1
    p2 = m_ClippingLine[1];//线段端点2
    bool code1,code2,code3;
    code1 = judgePointInnerOrOuter(p1, m_window);//m_window中存储的矩形一条对角线的两个端点，是一个数组
    code2 = judgePointInnerOrOuter(p2, m_window);
    CPoint out1, out2;
    CPoint inn1,inn2;
    CPoint mid;
    int d1,d2;

    //两个端点都在框内
    if(code1&&code2)
    {
        inn1 = p1;inn2 = p2;
    }
    //只有一个端点在框内
    if((code1==true&&code2==false)||(code1==false&&code2==true))
    {
        if(code1){
            out1 = p2;
            inn2 = inn1 = p1;
        }else{
            out1 = p1;
            inn2 = inn1 = p2;
        }
        inn1 = bSearch(out1,inn1,m_window);//折半找交点
    }

    //两个端点都在框外
    if(code1 == false && code2 == false)
    {
        out1=p1;out2=p2;
        CPoint point1,point11,point2,point22;
        point1 = m_window[0];point11 = m_window[1];
        point2.x = m_window[0].x;point2.y = m_window[1].y;
        point22.x = m_window[1].x;point22.y = m_window[0].y;
        //判断线段与对角线是否有交点
        bool code4 = judgeLineToLine(out1,out2,point1,point11);
        bool code5 = judgeLineToLine(out1,out2,point2,point22);
        if(code4||code5){
            //求线段与对角线的交点r
            CPoint r;
            if(code4)
                r = getPoint(out1,out2,point1,point11);
            else
                r = getPoint(out1,out2,point2,point22);
            inn1 = inn2 = r;
            inn1 = bSearch(out1,inn1,m_window);
            inn2 = bSearch(out2,inn2,m_window);
        }
        else {//线段与框没有交点
            inn1 = NULL;
            inn2 = NULL;
        }
    }
    //最后线段与矩形交点的结果
    m_ClippedLine[0].x = inn1.x;
    m_ClippedLine[0].y = inn1.y;
    m_ClippedLine[1].x = inn2.x;
    m_ClippedLine[1].y = inn2.y;
    myClipDone = true;//这个不用管
}