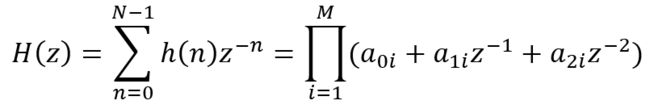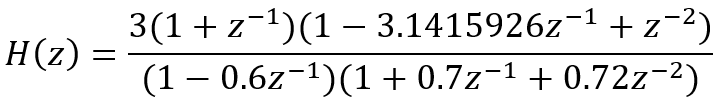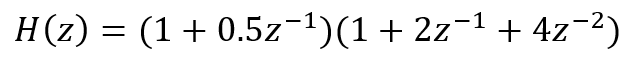数字滤波器(一)--IIR与FIR的基本结构与MATLAB实现

前言

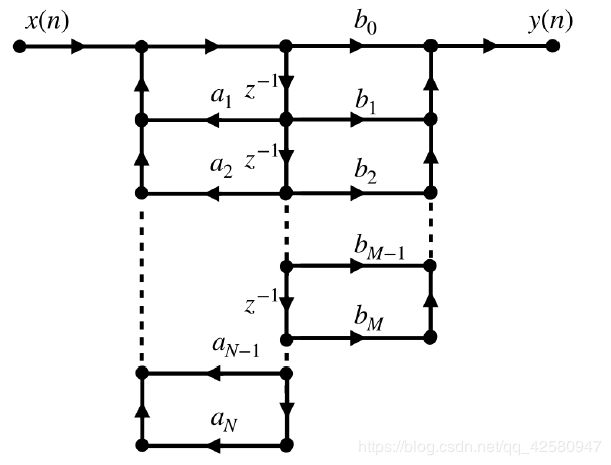
常用的数字滤波器包括IIR与FIR，常用的表示方法有以下几种形式：差分方程、单位序列响应$h(n)$ ,系统函数$H(z)$以及系统框图，本篇博文着重以系统框图的形式来讲述IIR与FIR。基础的系统框图如图1所示：

图1. 数字滤波器基本框图的表示

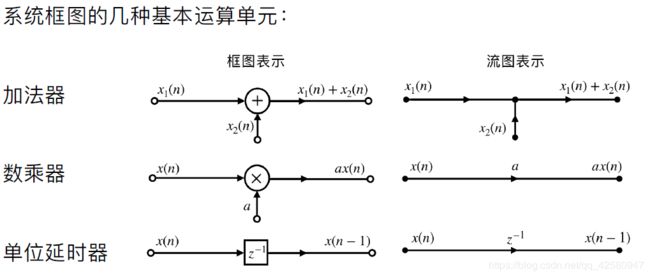
由于本文中会涉及滤波器零极点的知识，所以先列举一下零极点对一个滤波器的影响：

• 零极点对于幅频特性的影响

  • 零点控制幅频响应的峰谷，零点越接近于单位圆，峰谷值越小，当零点在单位圆上时，n对应点幅频特性值为零。

  • 极点控制幅频特性的峰值，极点越接近于单位元，峰值越大，极点在单位圆上时，系统不稳定。

  • 在原点处的零极点不改变系统的幅频特性。

• 零极点对于相频特性的影响
  • 在幅频特性不变得情况下，当系统的零点全部在单位圆内部时，所得到系统为最小相位系统；系统的零点全部在单位圆之外，所得到为最大相位系统。

1. 无限长单位冲激响应滤波器IIR

1.1 IIR的定义和特点

IIR(Infinite-duration Impulse Responses)即无限长冲激响应响应滤波器，其特点是：

• 单位冲激响应$h(n)$为无限长序列
• 系统函数$H(z)$在有限z平面内存在极点，其一般形式为：
  
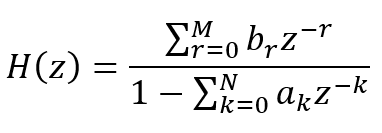
• 系统在结构上存在反馈，也就是说当前系统的输出和之前系统的输入和输出都有关系，根据系统函数$H(z)$，可以得到IIR的差分方程为：
  
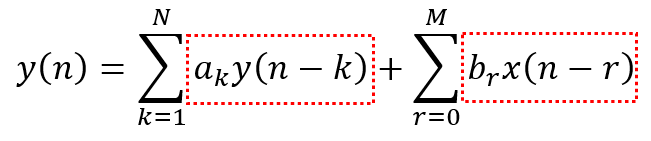
  通过上式可以发现，IIR系统符合递归型结构。

1.2 IIR的基本结构

IIR的基本结构分为直接Ⅰ型、直接Ⅱ型、级联型与并联型结构。

• 直接Ⅰ型结构
  根据IIR的差分方程，我们可以直接列出IIR的结构，如图1.1所示，左边的部分提供零点，就是差分方程中的
  
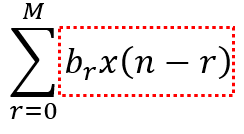
  图1.1右边的部分提供极点，就是差分方程中的
  
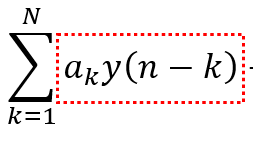
  该结构的滤波器共有N+M个延时单元：
  

图1.1 IIR的直接Ⅰ型结构

• 直接Ⅱ型结构
  直接Ⅱ型结构相当于将直接型Ⅰ结构的左右两个部分互换位置并且共享了延时单元，结构图如图1.2所示：
  

图1.2 IIR的直接Ⅱ型结构

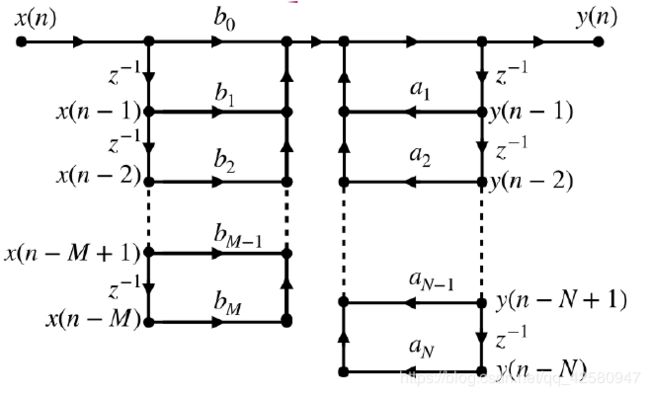
直接Ⅱ型只需要N个延时单元即可，比直接Ⅰ型少M个，计算起来更简单一些，对于直接Ⅰ型和直接Ⅱ型的结构，优点是简单直观，缺点就是系数对滤波器的控制关系不明显(零极点不明显，难以调整)

• 级联型结构
  我们可以将系统函数拆分成多个子函数成绩的形式，即：
  
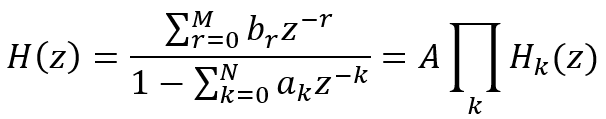
  将$H_k(z)$称为二阶基本节，它的一般形式为：
  
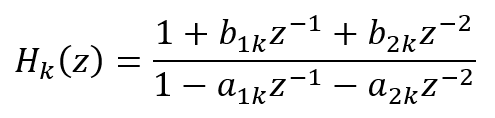
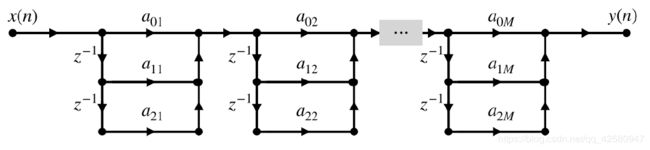
  该形式的特点是有两个极点，每一个实系数的二阶数字滤波器$H_k(z)$的结构均可以用直接Ⅱ型结构，将子函数所代表的系统级联起来即可以得到$H(z)$的级联型结构，如图1.3h所示：
  
  

图1.3 级联型结构

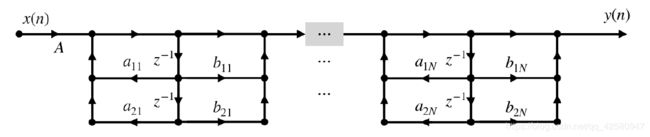
级联型结构有这几个特点：调整零极点结构方便；运算误差比直接型小，但是误差会逐级积累。

• 并联型结构
  对于并联型结构我们可以将系统函数拆分成多个子函数之和的形式，即：
  
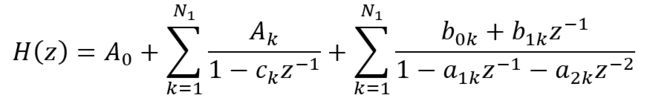
  该结构由$N_1$个一阶基本节，$N_2$个二阶基本节以及常数$A_0$并联而成。其基本结构如图1.4所示：
  
  

图1.4 并联型结构

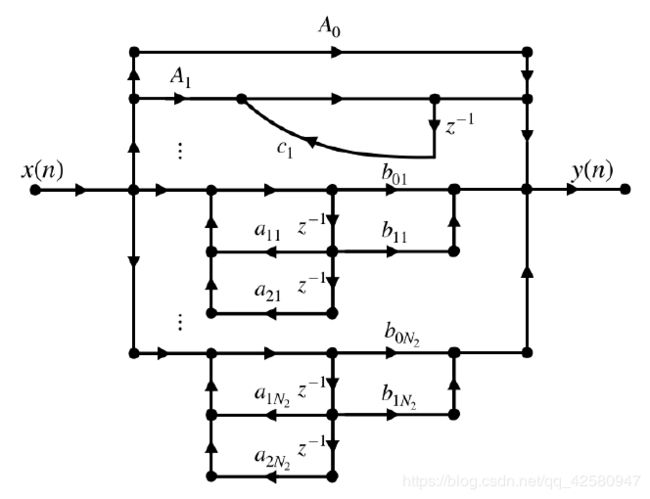
并联型结构的特点是：子系统的误差不相互影响；并联可单独调整极点，单不能调整零点。

2. 有限长单位冲激响应滤波器FIR

2.1 FIR的特点

FIR(Finite-duration Impulse Responses)滤波器即有限长单位冲激响应滤波器，其特点是：

• 单位冲激响应$h(n)$为有限长序列
• 系统函数$H(z)$在有限z平面内不存在极点，其一般形式为关于z的多项式，FIR的一般形式为：
  
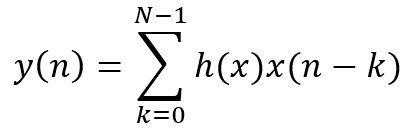
• 一般属于非递归系统，不存在反馈
• 可以设计成具有线性相位的形式

2.2 FIR的基本结构

FIR的基本结构包括直接型、

• 直接型结构
  根据FIR的差分方程：
  
  可以作出直接型框图如图1.1所示：
  

图2.1 直接型FIR结构

• 级联型结构
  根据FIR系统函数
  
  可以将系统转化为二阶基本节的级联，每个二阶基本节用直接型结构实现，则信号流图如图2.2所示：
  

图2.2 级联型FIR结构

该结构的优点是便于控制零点，缺点是所需系数较多，所需的乘法较多。

• 快速卷积型结构
  根据快速卷积的算法原理：
  
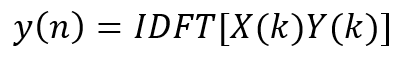
  其中$X(k)$,$Y(k)$分别是$x(n)$,$y(n)$的L点DFT，因此快速卷积型结构如图2.3下：
  

图2.3 快速卷积型FIR结构

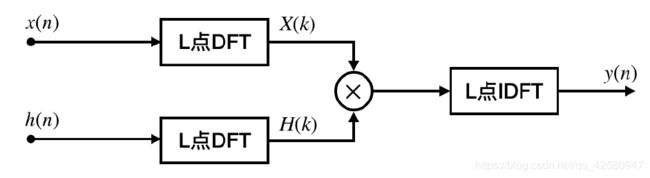
• 线性相位FIR结构
  • 线性相位的定义：滤波器对不同频率的正弦波所产生的相移和正弦波的频率具有线性关系
  • 线性相位的因果FIR系统的单位序列响应特性：单位序列响应满足$h(n)=\pm h(N-1-n)$,其中N代表序列的长度。
    其中$h(n)=-h(N-1-n)$代表$h(n)$关于$\frac{N-1}{2}$奇对称；
    $h(n)=h(N-1-n)$代表$h(n)$关于$\frac{N-1}{2}$偶对称；

关于线性相位FIR结构，后续会有专门的一篇博文来介绍。

3. MATLAB实现

3.1 IIR滤波器的实现

• 直接型滤波器的实现
  在实现滤波器之前我们需要先写一个单位冲激函数，相关代码如下：

function x = impseq(n0, n1, n2)
% impseq：产生一个冲激函数
% 参数：在n0-n2之间，n1处为1，其余为0
% 返回： x是冲激序列
    n = n0:n2;
    x = [(n-n1) == 0];
end 

然后我们就可以实现直接型滤波器了，直接型滤波器是后面几种类型的基础，级联型和并联型都可以由直接型转化而来，我们要实现的滤波器的系统传递函数如下所示，求出该滤波器的单位冲激响应和单位阶跃响应：

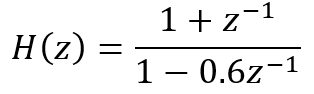
% 直接型IIR滤波器实现

% 系统传递函数的分子系数
b = [1, 1];

% 系统传递函数的分母系数
a = [1, -0.6];

% 单位冲激响应h(n)
N = 30;
delta = impseq(0, 0, N);
h = filter(b, a, delta);

% 输入为单位阶跃响应
X = [ones(1,5), zeros(1, N-5)];

% 对应得输出
y = filter(b, a, X);

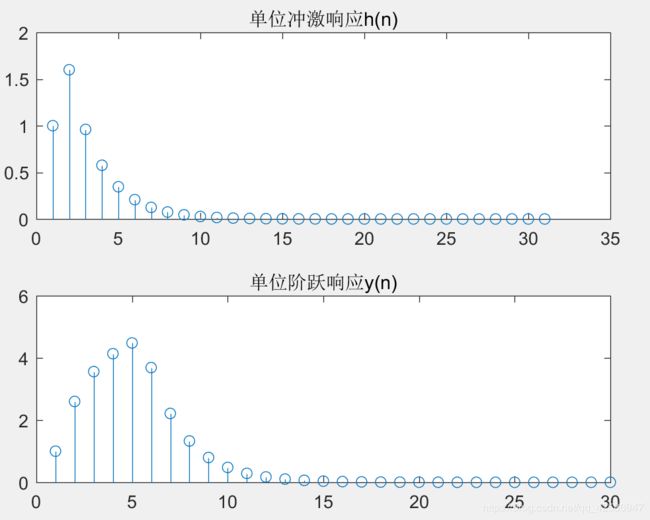
% 绘图
subplot(211); stem(h); title('单位冲激响应h(n)');
subplot(212); stem(y); title('单位阶跃响应y(n)');

输出结果为：

• 级联型滤波器的实现
  我们要实现的滤波器的系统传递函数如下所示，求出该滤波器的单位冲激响应和单位阶跃响应：
  
  我们将级联型结构的滤波器写到一个函数里面：

function y = casfilter(b0, B, A, X)
% casfilter: 级联型IIR滤波器的实现
% 参数：
% b0: 增益系数
% B: 系统传递函数的分子系数矩阵
% A: 系统传递函数的分母系数矩阵 
% X: 输入序列
% y: 经过滤波器的输出序列

    % 得到系数矩阵的维度，K行，L列
    [K, L] = size(B);
    
    % 得到输入序列的长度
    N = length(X);
    
    % 建立K+1行，N列的零矩阵
    % 该矩阵第一行存放输入序列，第二行存放经过第一个级联节点的输出序列，第i行存放
    % 经过第i-1个级联节点的输出序列，第K+1行存放最终的输出序列
    w = zeros(K+1, N);
    
    % 令第一个行等于输入序列
    w(1,:) = X;
    
    % 计算每一个级联节点的输出序列并作为下一级的输入序列
    for i = 1:1:K
        w(i+1,:) = filter(B(i,:), A(i,:),w(i,:));
    end
    
    % 最终的滤波结果为最后的输出序列乘上增益系数
    y = b0*w(K+1, :);
end

下面我们对目标滤波器进行实现：

% 级联型IIR滤波器

% 初始化参数
b0 = 3;                  % 增益系数
N =30;                   % 输入序列长度
B = [1, 1, 0;
     1, -3.1415926, 1];  % 系统传递函数的分子系数矩阵
A = [1, -0.6, 0;
     1, 0.7, 0.72];      % 系统传递函数的分母系数矩阵

% 获得单位冲激序列
delta = impseq(0, 0, N);

% 获得单位阶跃序列
X = [ones(1, 5), zeros(1, N-5)];

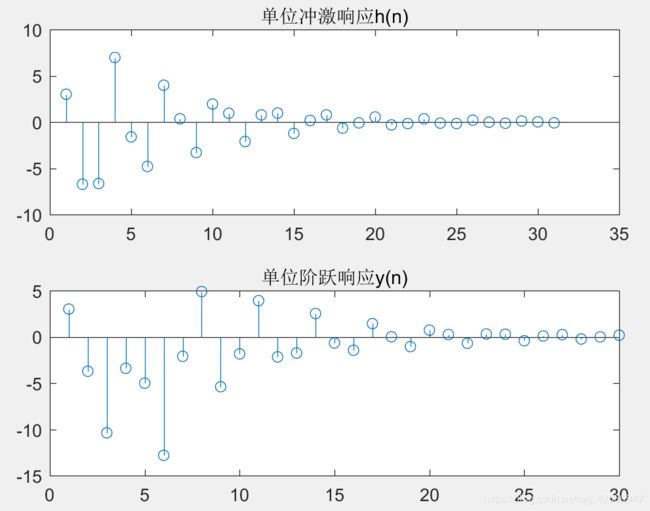
% 该滤波器的单位冲激响应
h = casfilter(b0, B, A, delta);

% 该滤波器的单位阶跃响应
y = casfilter(b0, B, A, X);

% 绘制曲线
subplot(211); stem(h); title('单位冲激响应h(n)');
subplot(212); stem(y); title('单位阶跃响应y(n)');

MATLAB的输出结果为：

• 并联型滤波器的实现
  我们将并联型滤波器用一个函数实现：

function y = parfilter( C, B, A, X )
% casfilter: 并联型IIR滤波器的实现
% 参数：
% C: B的长度等于A的长度时，多项式的部分, 大部分时候为0
% B: 系统传递函数的分子系数矩阵
% A: 系统传递函数的分母系数矩阵 
% X: 输入序列
% y: 经过滤波器的输出序列

    % 得到系数矩阵的维度，K行，L列 
    [K, L] = size(B);
    
     % 得到输入序列的长度
    N = length(X);
    
    % 建立K+1行，N列的零矩阵
    w = zeros(K+1, N);
    w(1,:) = filter(C, 1, X);
    
    % 单独计算每一个并联联节点的输出序列
    for i = 1:1:K
        w(i+1,:) = filter(B(i,:),A(i,:),X);
    end
    
    % 将所有并联节点的输出相加即最后的输出结果
    y = sum(w);

end

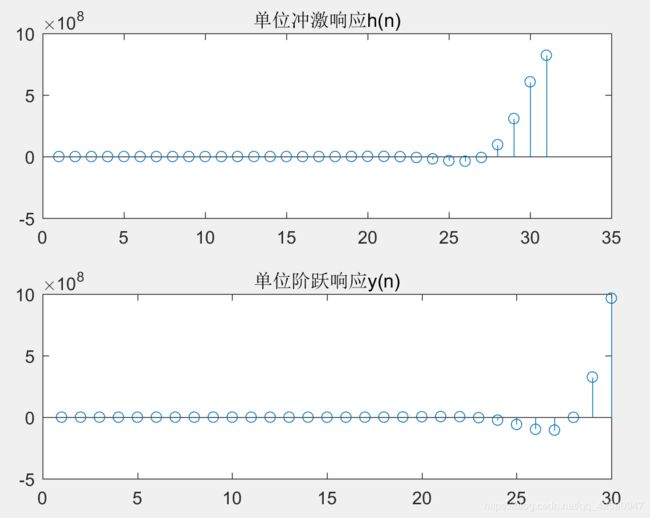
下面我们来实现下面这个滤波器的单位冲激响应和单位阶跃响应：

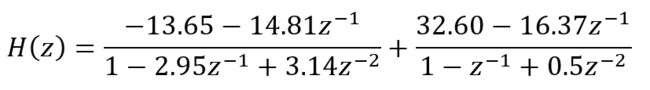
代码如下：

% 并联型IIR滤波器

% 初始化参数
C = 0;                 
N =30;                   % 输入序列长度
B = [-13.65, -14.81;
     32.60, -16.37];  % 系统传递函数的分子系数矩阵
A = [1, -2.95, 3.14;
     1, -1, 0.5];      % 系统传递函数的分母系数矩阵

% 获得单位冲激序列
delta = impseq(0, 0, N);

% 获得单位阶跃序列
X = [ones(1, 5), zeros(1, N-5)];

% 该滤波器的单位冲激响应
h = parfilter(C, B, A, delta);

% 该滤波器的单位阶跃响应
y = parfilter(C, B, A, X);

% 绘制曲线
subplot(211); stem(h); title('单位冲激响应h(n)');
subplot(212); stem(y); title('单位阶跃响应y(n)');

运行结果如下：

3.2 FIR滤波器的实现

• 直接型滤波器的实现
  FIR的直接型滤波器和IIR的直接型滤波器非常相似，将IIR直接型滤波器的系统传递函数的字母变为1就是FIR的直接型滤波器。
  我们现在来实现滤波器：
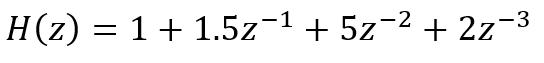  的单位冲激响应和单位阶跃响应。

% 直接型FIR滤波器实现

% 系统传递函数的分子系数
b = [1, 1.5, 5, 2];

% 系统传递函数的分母系数，IIR的分母变为1就是FIR
a = 1;

% 单位冲激响应h(n)
N = 30;
delta = impseq(0, 0, N);
h = filter(b, a, delta);

% 输入为单位阶跃响应
X = [ones(1,5), zeros(1, N-5)];

% 对应得输出
y = filter(b, a, X);

% 绘图
subplot(211); stem(h); title('单位冲激响应h(n)');
subplot(212); stem(y); title('单位阶跃响应y(n)');

MATLAB输出为：

• 级联型滤波器的实现
  FIR的级联型滤波器和IIR的级联型滤波器非常相似，将IIR级联型滤波器的系统传递函数的字母变为1就是FIR的级联型滤波器。
  们现在来实现滤波器：
  
  的单位冲激响应和单位阶跃响应。

% 级联型FIR滤波器

% 初始化参数
b0 = 1;                  % 增益系数
N =30;                   % 输入序列长度
B = [1, 0.5, 0;
     1, 2, 4];           % 系统传递函数的分子系数矩阵
A = [1, 0, 0;
     1, 0, 0];      % 系统传递函数的分母系数矩阵

% 获得单位冲激序列
delta = impseq(0, 0, N);

% 获得单位阶跃序列
X = [ones(1, 5), zeros(1, N-5)];

% 该滤波器的单位冲激响应
h = casfilter(b0, B, A, delta);

% 该滤波器的单位阶跃响应
y = casfilter(b0, B, A, X);

% 绘制曲线
subplot(211); stem(h); title('单位冲激响应h(n)');
subplot(212); stem(y); title('单位阶跃响应y(n)');

输出结果为：