GAMES101-现代计算机图形学学习笔记（03）

GAMES101-现代计算机图形学学习笔记（03）

原课程视频链接以及官网
b站视频链接: link.
课程官网链接: link.

变换

为什么要有变换

从坐标变换来说，当一个物体生成时，它是位于自身局部空间。如果我们需要在一个整体的坐标系上去摆弄我们的不同的物体，去调整它们之间的相对位置，就需要一个model矩阵将它们变换到一个统一的坐标系下，也称世界坐标系。当我们玩一些第一人称游戏时，我们的视角可以看成是一个摄像机，而要以一个摄像机的视角去观察世界时，还需要view矩阵将坐标变换到相机空间。当将三维物体投影在二维屏幕像素上时，还需要进行投影以及视口变换…从物体变换的角度来说，我们在建模时需要对物体进行缩放，平移，旋转等操作，这些也属于变换。
总的来说，变换是图形学中必不可少的一部分。

二维变换

缩放

设左图坐标为（x,y）,右图坐标为（x’，y’），所以可以得到如下公式来计算缩放：

$$\begin{array}{rl}& x^{\prime }=sx\\ & y^{\prime }=sy\end{array}\to \left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$$
也可以通过修改缩放矩阵 $S=\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]$ 中的某个分量来达到只缩放某个轴的效果。

镜像

设左图坐标为（x,y）,右图坐标为（x’，y’），所以可以得到如下公式来计算镜像：
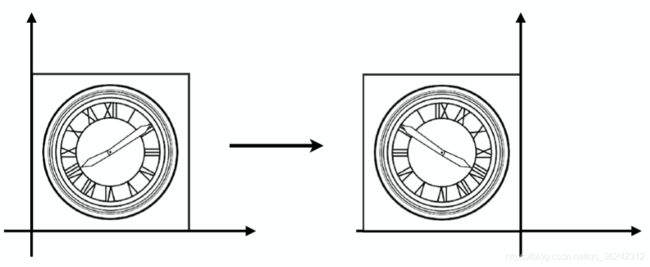$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$$

错切

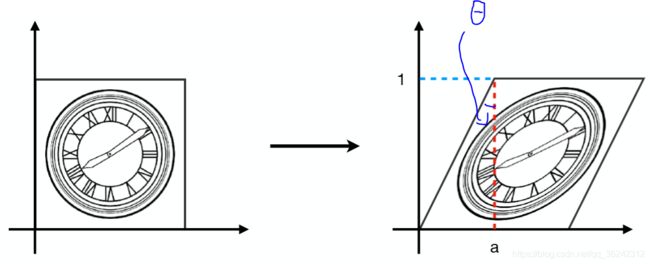
设左图坐标为（x,y）,右图坐标为（x’，y’）。假设x方向平移量为a，图中夹角为θ，考虑x方向上的错切，其计算公式为（仅仅针对于顶边x）：
$$\{\begin{array}{l}{x}^{\prime }=x+y\cdot \tan \theta \\ y^{\prime }=y\end{array}$$y坐标不变，所以 y’ = y，且有 $a=y\cdot \tan \theta$，y=1， 将其带入可得到：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$$

同理y方向上的错切公式可以得出（仅仅针对于顶边）：
$$\{\begin{array}{l}{x}^{\prime }=x\\ y^{\prime }=y+x\cdot \tan \theta \end{array}$$$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}1& 0\\ tan\theta & 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$$

旋转

设左图坐标为（x,y）,右图坐标为（x’，y’）。

设求解旋转公式为：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$$
先将点（1,0）带入分别左右图有
$$\{\begin{array}{l}{x}^{\prime }=a=\cos \theta \\ y^{\prime }=c=\sin \theta \end{array}$$
同时将点（0,1）带入分别左右图有
$$\{\begin{array}{l}{x}^{\prime }=b=-\sin \theta \\ y^{\prime }=d=\cos \theta \end{array}$$
所以解得二维空间上的旋转矩阵为：
$${\mathbf{R}}_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

齐次坐标

①引入原因：
上述变换本质上都是线性变换，即：
$$\begin{array}{rl}{x}^{\prime }& =ax+by\\ y^{\prime }& =cx+dy\\ \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]& =\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]\end{array}$$
而当计算平移变换的时候会多加一个向量，即：
$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]+\left[\begin{array}{l}{t}_x\\ t_y\end{array}\right]$$
为了统一变换形式，设计者通过添加了一个维度信息来统一平移变换和其他变换，这种方法使得平移分量可以直接嵌入进变换矩阵，即：
$$\left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right)=\left(\begin{array}{lll}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right)\cdot \left(\begin{array}{l}x\\ y\\ 1\end{array}\right)=\left(\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right)$$
同时，设计者也通过向点和向量添加多一个维度信息来使得矩阵相乘可以对齐。通过这个多一维（w维）的信息也可以用于区分点和向量，并做透视除法，具体如下：
2D point $=(x,y,1{)}^{\top }$
2D vector $=(x,y,0{)}^{\top }$
可以想到，当点与点做减法时，w维度为0，刚好符合向量定义。同时如果点w分量不为1，也可以将其除以w，也等同于后面的透视除法。

逆变换

当我们需要做一个变换的逆变换时，只需要将其初始变换矩阵取逆，然后乘以坐标即可。本质上可以看做$A\cdot A^{-1}=1$来抵消这次变换。
（旋转矩阵的正交性对于逆变换特别友好，由于旋转矩阵是正交矩阵，其逆为对应的转置矩阵，所以只需要将其取转置即可）
（如何证明旋转矩阵是正交矩阵：可以想象绕x轴正向旋转θ角度和绕x轴逆向旋转θ角度是相反的，我们只需要将旋转矩阵中的θ分量取负，然后根据cos 和 sin 的性质，即可得到其逆为转置，其中旋转矩阵的定义为${\mathbf{R}}_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$）

变换的组合

变换可以根据各种各样的变换组合得到，比如先平移，再旋转的公式为$V^{\prime }=M_{rotate}\ast M_{trans}\ast V$ ，其中V为坐标点。不过在组合的时候要注意顺序，如果先平移，再旋转，那么旋转中心移走，即不是绕原点旋转。如果想要绕原点旋转，我们需要先将顶点坐标统一平移到原点，然后旋转，再平移到初始位置。